Density of Black Holes
- Page ID
- 49956
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Densities of matter vary widely, from the density of interstellar gases (~10-22 assuming 90% H, 10% He; variable T) to that of an earth-mass black hole, whose theoretical mean density inside the Schwarzschild radius is about 4 × 1014 g/cm3.

The Schwarzschild radius is the "point of no return" - once you get closer to the black hole than that, you can never escape. The theoretical density of a black hole depends on how big it is and how you define its size. The density at the center of a black hole is infinite (it's a famous "singularity"[1], which leads to difficulties in modern cosmology).
On Earth, densities range from 10-4 g/cm3 for light gases to 0.001 g/cm3 for aerogels and up to the heaviest substance, osmium, with a density of 22.61 g/cm3. The terms heavy and light are commonly used in two different ways. We refer to weight when we say that an adult is heavier than a child. On the other hand, something else is alluded to when we say that styrofoam is heavier than an aerogel. A small sample of styrofoam would obviously weigh less than a roomful of aerogel, but styrofoam is heavier in the sense that a piece of given size weighs more than the same-size piece of balsa.
| Material | ρ / g/cm3 |
|---|---|
| Interstellar medium | 10-22 − 10-12 |
| Earth's atmosphere | 0.0012 |
| Aerogel | 0.001 − 0.002 |
| Styrofoam | 0.030 − 0.120 |
| Cork | 0.220 − 0.260 |
| Water | 1.000 |
| Plastics | 0.850 − 1.400 |
| Aluminum | 2.7 |
| The Earth (mean) | 5.5153 |
| Copper | 8.920 − 8.960 |
| Lead | 11.340 |
| osmium | 22.61 |
| The Inner Core | ~13.000 |
| Uranium | 19.100 |
| Iridium | 22.500 |
| The core of the Sun | ~150.000 |
| Atomic nuclei | ~3 × 1014 |
| Neutron star | 8.4 × 1013 − 1 × 1015 |
| Black hole | 4 × 1014 |
Densities of many more materials are easily found.
What we are actually comparing is the mass per unit volume, that is, the density. In order to determine these densities, we might weigh a cubic centimeter of each material. If the styrofoam weighed 0.10 g and the aerogel 0.001 g, we could describe the density of styrofoam as 0.10 g cm–3 and that of an aerogel as 0.001 g cm–3. (Note that the negative exponent in the units cubic centimeters indicates a reciprocal. Thus 1 cm–3 = 1/cm3 and the units for our densities could be written as 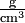 , g/cm3, or g cm–3. In each case the units are read as grams per cubic centimeter, the per indicating division.) We often abbreviate "cm3" as "cc", and 1 cm3 = 1 mL exactly, by definition.
, g/cm3, or g cm–3. In each case the units are read as grams per cubic centimeter, the per indicating division.) We often abbreviate "cm3" as "cc", and 1 cm3 = 1 mL exactly, by definition.
In general it is not necessary to weigh exactly 1 cm3 of a material in order to determine its density. We simply measure mass and volume and divide volume into mass:
\[\text{Density} = \dfrac{\text{mass}} {\text{volume}}\]
or
\[\rho = \dfrac{\text{m}} {\text{V}}\]
where ρ = density m = mass V = volume
Example \(\PageIndex{1}\): Density of a Black Hole
What is the density of a black hole?
A black hole contains about 3.7M (3.7 million) solar masses (a solar mass is 1.98892 × 1033 grams) and is assumed to be a sphere with a Schwarzschild radius of 3x105 cm x (M / Msun) where M is the mass of the black hole and Msun is the mass of the Sun. Typically, M for a black hole in our galaxy is around 10 times the mass of the Sun, but for supermassive black holes at the centers of galaxies it can be millions or even billions [3]. What is its density?
Solution
You can use the Schwarzschild radius to calculate the "density" of the black hole - i.e., the mass divided by the volume enclosed within the Schwarzschild radius.
The radius of the sphere must be calculated first, using the formula 3x105 cm x (M / Msun) we get 3x105 cm x 3.7 × 106 = 1.125 × 1012
\[\text{V} = \dfrac{4}{3} \pi \text{r}^3 = \dfrac{4}{3} \times \text{3.142} \times (\text{1.125} \times \text{10}^{12} \text{cm})^3 = \text{5.964} \times \text{10} ^{36} \text{cm}^3 \nonumber\]
The mass of the sphere is 3.7 x 106 Msun × 1.98892 × 1033 g/Msun = 7.359 × 1039 g
\[ \begin{align*} \text{Density} =\rho &= \dfrac{\text{m}} {\text{V}} \\[4pt] &= \dfrac{\text{7.359} \times \text{10}^{39}}{\text{5.964} \times \text{10}^{36}} = \text{1.31} \times \text{10}^3 \dfrac{\text{g}}{\text{cc}} \end{align*}\]
You might have recognized a shortcut: the density is
\[(\text{1.8} \times \text{10}^{16} \dfrac{\text{g}}{\text{cm}^3}) \times (\dfrac{\text{M}_{sun}}{\text{M}})^2 \nonumber\]
or
\[\text{1.8} \times \text{10}^{16}\dfrac{\text{g}}{\text{cm}^3} \times (\dfrac{1}{\text{3.7} \times \text{10}^6})^2 = \text{1.31} \times \text{10}^3 \dfrac{\text{g}}{\text{cc}} \nonumber\]
From the point of view of an outside observer, this might as well be the actual black hole density, since the distribution of matter within the Schwarzschild radius has no effect on the outside.
Example \(\PageIndex{2}\): Black Hole and an Atom
There is a rough analogy between a black hole and an atom. In both cases, the mass is concentrated in a tiny region at the center, but the "size" of the object is much bigger. The radius of a nucleus is (r = A1/3 x 1.7 x 10-13 cm), where A is the mass number of the nucleus. The radius of the whole atom is on the order of 100-200 pm (10-8 cm, 105 times as large, so all the mass of an atom resides in ~10-12% of its volume).
- What is the volume of an aluminum-27 nucleus?
- What is the mass of an aluminum nucleus in grams, if each particle has a mass of ~1 amu (1.6 x 10-27 g) and the mass deficit is ignored?
- What is the density of the Al nucleus, in g/cm3
Solution
- \(\text{r} = (\text{27})^{\dfrac{1}{3}} \times \text{1.7} \times \text{10}^{-13} \text{cm} = \text{5.1} \times \text{10}^{-13} \text{cm V} = \dfrac{4}{3} \pi \text{r}^3 = \text{5.56} \times \text{10}^{-37} \text{cm}^3\)
- \(\text{m} = \text{27} \times \text{1.6} \times \text{10}^{-24} \text{g} = \text{4.32} \times \text{10}^{-23} \text{g}\)
- \(\text{D} = \dfrac{\text{m}}{\text{V}} = \dfrac{\text{4.32} \times \text{10}^{-23} \text{g}}{\text{5.56} \times \text{10}^{-37} \text{cm}^3} = \text{7.77} \times \text{10}^{13} \dfrac{\text{g}}{\text{cm}^3}\)
Example \(\PageIndex{3}\): Density Calculation
Calculate the density of
- a piece of aluminum whose mass is 37.42 g and which, when submerged, increases the water level in a graduated cylinder by 13.9 ml
- an aluminum cylinder of mass 25.07 g, radius 0.750 cm, and height 5.25 cm.
Solution
a) Since the submerged metal displaces its own volume,
\[\text{Density} =\rho = \dfrac{\text{m}} {\text{V}} = \dfrac{37.42 g} {13.9 mL} = \text {2.69 g/mL or 2.69 g mL}^{-1}\]
b) The volume of the cylinder must be calculated first, using the formula
\[\text{V} = {\pi} r^{2} h = 3.142 × \text{(0.750 cm)}^{2} * 5.25 \text{cm} = \text{9.278 718 8 cm}^{3}\]
Then
\[\begin{align*} \rho = \dfrac{\text{m}} {\text{V}} = \dfrac{25.07g} {9.278 718 8cm^{3}} \\[4pt] &= \text{2.70} \dfrac{\text{g}}{\text{cm}^3} \end{align*}\]
Note that unlike mass or volume, the density of a substance is independent of the size of the sample. Thus density is a property by which one substance can be distinguished from another. A sample of pure aluminum can be trimmed to any desired volume or adjusted to have any mass we choose, but its density will always be 2.70 g/cm3 at 20°C. The densities of some common pure substances are listed in the Table.
Tables and graphs are designed to provide a maximum of information in a minimum of space. When a physical quantity (number × units) is involved, it is wasteful to keep repeating the same units. Therefore it is conventional to use pure numbers in a table or along the axes of a graph. A pure number can be obtained from a quantity if we divide by appropriate units. For example, when divided by the units gram per cubic centimeter, the density of aluminum becomes a pure number 2.70:
\[\dfrac{\text{Density of aluminum}} {\text{1 g cm}^{-3}} = \dfrac{\text{2.70 g cm}^{-3}} {\text{1 g cm}^{-3}} = 2.70\]
Therefore, a column in a table or the axis of a graph is conveniently labeled in the following form:
\[\dfrac{\text{Quantity}}{\text{units}}\]
This indicates the units that must be divided into the quantity to yield the pure number in the table or on the axis. This has been done in the second column of the Table.
Converting Densities
In our exploration of Density, notice that chemists may express densities differently depending on the subject. The density of pure substances may be expressed in kg/m3 in some journals which insist on strict compliance with SI units; densities of soils may be expressed in lb/ft3 in some agricultural or geological tables; the density of a cell may be expressed in mg/µL; and other units are in common use. It is easy to transform densities from one set of units to another, by multiplying the original quantity by one or more unity factors:
Example \(\PageIndex{4}\): Density Conversion
Convert the density of water, 1 g/cm3 to
- lb/cm3 and
- lb/ft3
Solution
a. The equality 454 g = 1 lb can be used to write two unity factors,
\(\dfrac{\text{454 g}} {\text{1lb}}\) or \(\dfrac{\text{1 lb}} {\text{454}}\)
The given density can be multiplied by one of the unity factors to get the desired result. The correct conversion factor is chosen so that the units cancel:
\(\dfrac{\text{1 g}} {\text{cm}^{3}}* \dfrac{\text{1 lb}} {\text{454 g}} = 0.002203 \dfrac{\text{lb}} {\text{cm}^{3}}\)
b. Similarly, the equalities 2.54 cm = 1 inch, and 12 inches = 1 ft can be use to write the unity factors:
\(\dfrac{\text{2.54 cm}} {\text{1 in}}\), \(\dfrac{\text{1 in}} {\text{2.54 cm}}\), \(\dfrac{\text{12 in}} {\text{1 ft}}\) and \(\dfrac{\text{1 ft}} {\text{12 in}}\)
In order to convert the cm3 in the denominator of 0.002203 \(\dfrac{lb} {cm^{3}}\) to in3, we need to multiply by the appropriate unity factor three times, or by the cube of the unity factor:
\(\text{0.002203} \dfrac{\text{g}} {\text{cm}^{3}}\) x \(\dfrac{\text{2.54 cm}} {\text{1 in}}\) x \(\dfrac{\text{2.54 cm}} {\text{1 in}}\) x \(\dfrac{\text{2.54 cm}} {\text{1 in}}\)
or
\(\text{0.002203} \dfrac{\text{g}} {\text{cm}^{3}}\) x \((\dfrac{\text{2.54 cm}} {\text{1 in}})^{3} = \text{0.0361} \dfrac{\text{lb}}{\text{in}^3}\)
This can then be converted to lb/ft3:
\(\text{0.0361} \dfrac{\text{lb}} {\text{in}^{3}}\) x \((\dfrac{\text{12 in}} {\text{1ft}})^{3} = \text{62.4} \dfrac{\text{lb}}{\text{ft}^3}\)
It is important to notice that we have used conversion factors to convert from one unit to another unit of the same parameter
References
- en.Wikipedia.org/wiki/Gravitational_singularity
- en.Wikipedia.org/w/index.php?title=Density
- http://curious.astro.cornell.edu/que...php?number=219
Contributors and Attributions
Ed Vitz (Kutztown University), John W. Moore (UW-Madison), Justin Shorb (Hope College), Xavier Prat-Resina (University of Minnesota Rochester), Tim Wendorff, and Adam Hahn.


