2.02: LFT and Frontier Molecular Orbital Theory
- Page ID
- 210942
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)In this post, we’ll begin to explore the molecular orbital theory of organometallic complexes. Some background in molecular orbital theory will be beneficial; an understanding of organic frontier molecular orbital theory is particularly helpful. Check out Fukui’s Nobel Prize lecture for an introduction to FMO theory. The theories described here try to address how the approach of ligands to a transition metal center modifies the electronics of the metal and ligands. The last post on geometry touched on these ideas a little, but we’ll dig a little deeper here. Notably, we need to address the often forgotten influence of the metal on the ligands—how might a metal modify the reactivity of organic ligands?
Ligand Field Theory
The ligand field theory (LFT) fleshes out the ideas of crystal field theory with molecular orbital theory concepts. It provides a method for understanding M–L bonding and antibonding orbitals; however, it has been strongly disputed by computational studies in favor of valence bond models that incorporate hypervalency. Still, LFT provides a more complete picture of complex bonding than crystal field theory, so we’ll discuss it here. Furthermore, the portions of LFT under dispute have nothing to do with CFT, so “no harm no foul.” Let’s take a look at the molecular orbitals of a hypothetical octahedral MLn complex to begin hashing out LFT.
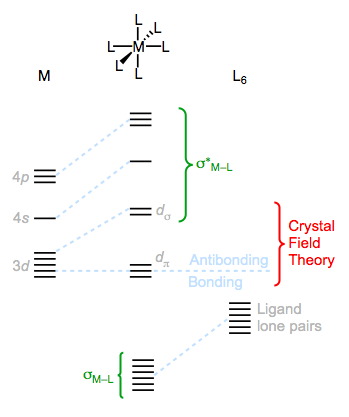
The M–L bonding molecular orbitals mostly have ligand character, while the antibonding orbitals mostly reside on the metal.
Notice that the perturbations of the metallic d orbitals are consistent with the ideas of crystal field theory for the octahedral geometry. The labels dσ and dπ will be useful for us later, and indicate how the d orbitals overlap with the incoming ligand orbitals—the dσ orbitals overlap in a head-on, sigma-type manner, and the dπ orbitals overlap in a side-on, pi-type manner. The dσ orbitals are destabilized through electrostatic repulsion, while the dπ orbitals essentially remain non-bonding. What LFT adds to these CFT ideas is a description of the fate of the remaining unfilled metal valence orbitals and the filled ligand orbitals. According to the LFT picture, orbital overlap between the 4s, 4p and symmetry-matched 4d (i.e., the 4dσ) AOs and the six ligand HOMOs results in six bonding and six antibonding MOs. Notice that the math works out:
1 4s + 3 4p + 2 3dσ + 6 ligand HOMOs = 6 bonding MOs + 6 antibonding MOs
As necessary, the number of atomic orbitals in (12) equals the number of molecular orbitals out (12). But more important than the number of MOs is the character of each orbital—where is the electron density primarily located in these MOs? Ligand field theory provides a logical answer: the bonding MOs primarily possess ligand character, while the antibonding MOs are primarily localized on the metal. The guiding principle here is that MOs are composed primarily of those AOs to which they are closest in energy. In the end, we arrive at a critically important, albeit expected insight: the metal is electrophilic (owner of many unfilled MOs) while the ligands are nucleophilic (owners of filled MOs).
This may seem like a relatively simple picture at first glance. All we did, it seems, was tack the 4s, 4p and ligand orbitals on to crystal field theory. Yet this groundwork is necessary to build a truly powerful theory of the electronic structure of organometallic complexes. Until now, we’ve considered only the HOMO of the ligands. What happens when we take the HOMO and LUMO of the ligands into account? Read on…
Frontier Molecular Orbital Theory
The frontier molecular orbitals of a compound are at the “frontier” of electron occupation—the highest-energy occupied and lowest-energy unoccupied molecular orbitals (the HOMO and LUMO). The HOMO is logically viewed as nucleophilic or electron donating, while the LUMO is electrophilic and electron accepting. Furthermore, both chemical reactions and resonance can be explained by interactions (overlap) between a filled HOMO and an empty LUMO on one or more molecules. FMO theory uses these foundational ideas to explain the structure and reactivity of molecules, and at least in organic chemistry, the theory has been insanely successful.
When it comes to organometallic complexes, we can gain considerable insight by noticing that orbitals on the frontier are usually the metallic d orbitals. In the figure above, assuming that the metal is d6, the frontier falls between the dπ and dσ orbitals. Without a need for any quantum chemical calculations (only CFT and the number of d electrons are required), we can thus begin to anticipate the shapes of the frontier orbitals of organometallic complexes! Combined with a solid understanding of organic FMO theory and the frontier orbitals of organic ligands, we can recognize important orbital interactions in organometallic complexes that can explain a wide variety of observations.
Before digging in to an example, let’s introduce some terminology commonly used by organometallic chemists related to FMO theory. The terms acidity and basicity are used in the context of FMO theory very broadly—prepare to expand your mind! Acidity refers to the desire of a ligand, metal center, or specific orbital to accept electron density (from any viable electron source, not just a Brønsted base). Basicity refers to the desire of a ligand, metal center, or specific orbital to donate electrons (to any viable electron sink, not just a Brønsted acid). FMO theory also distinguishes between σ-acids, σ-bases, π-acids, and π-bases. The first two, σ-X, want to accept or donate electrons in a σ-type fashion—that is, aligned head on with another orbital. The latter two, π-X, want to accept or donate electrons in a π-type fashion—that is, aligned side by side with another orbital. Most commonly, these terms are applied to ligands to indicate their expected behavior in a fancy-schmancy but quite descriptive way, and the terms can also be applied to the metal center.

Sigma and pi acids and bases, with their most reactive frontier MOs and typical electronic behavior.
Why are these designations useful? Let’s look at an example now. Tungsten(0) hexacarbonyl and the other metal(0) carbonyls are interesting species. Let’s deconstruct W(CO)6 to see why…

Tungsten(0) hexacarbonyl. Why doesn't it fall apart?
We can make a very good argument that this compound ought to fall apart as soon as it’s made. The complex is neutral, but the deconstructed ligands and metal are all neutral too, and entropy loves the right-hand side of the figure above. Yet, the complex is reasonably stable. Why?!
FMO theory provides a good answer: there is more to the W–CO bond than meets the eye. Let’s zoom in on the tungsten–carbon bond and explore what might be going on here. Like almost all metal–carbon bonds, we expect W and C to be bound primarily through an interaction between a filled non-bonding orbital on carbon (HOMO) and an empty dσ orbital on the metal (LUMO). That’s depicted below, and it’s typical organometallic FMO theory. Interactions like this help explain why, for instance, extremely electron-poor ligands like PF3 make horrible ligands and bind to metals very weakly.

A typical orbital interaction between a metal and an organic ligand. Par for the course.
The right-hand resonance structure, which depicts two bonds between tungsten and carbon, suggests that there is another bonding interaction between W and C…perhaps one where the LUMO of the ligand and the HOMO of the metal get involved? Can we draw a viable HOMO–LUMO interaction by reversing the typical roles of metal and ligand? The LUMO of the ligand is a π* orbital, and the HOMOs of the metal are the d orbitals not aligned along the octahedral axes (the dπ orbitals). The symmetry of these orbitals is just right! See the lower orbital interaction in the figure below.

There's a new interaction in town...and the metal is an electron donor in the pi-type interaction.
Please note that the tungsten atom is not rotated at all; two different d orbitals are depicted in the two interactions. The second role-reversing interaction is important for π-acidic ligands like carbon monoxide, and is called backbonding. The interesting thing about backbonding is that when considering it, we must imagine the metal as electron donor and the ligand as electron acceptor. There is an important lesson here: consider the HOMO and LUMO of both the metal and ligands and their possible interactions. When it comes to tungsten(0) carbonyl, donation from the electron-rich (or π-basic) metal center to the π-acidic CO ligands is what holds everything together!
Keep the fundamental ideas of FMO theory in mind as we move forward. Primarily, keep your mind open and remember that metal centers can act as electron donors toward acidic ligands, if the energetics and symmetry are right. We’re about to embark on an epic ligand survey, so we’ll have plenty of opportunities to apply these ideas!


