Hückel or Tight Binding Theory (old)
- Page ID
- 11575
Now, let’s examine what determines the energy range into which orbitals (e.g., pp orbitals in polyenes, metal, semi-conductor, or insulator; s or ps orbitals in a solid; or s or p atomic orbitals in a molecule) split. I know that, in our earlier discussion, we talked about the degree of overlap between orbitals on neighboring atoms relating to the energy splitting, but now it is time to make this concept more quantitative. To begin, consider two orbitals, one on an atom labeled A and another on a neighboring atom labeled B; these orbitals could be, for example, the 1s orbitals of two hydrogen atoms, such as Figure 2.9 illustrates.
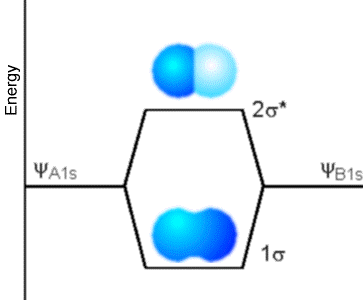
Figure 2.9. Two 1s orbitals combine to produce a s bonding and a s* antibonding molecular orbital
However, the two orbitals could instead be two pp orbitals on neighboring carbon atoms such as are shown in Fig. 2.10 as they form p bonding and p* anti-bonding orbitals.
Figure 2.10. Two atomic pp orbitals form a bonding p and antibonding p* molecular orbital.
In both of these cases, we think of forming the molecular orbitals (MOs) fk as linear combinations of the atomic orbitals (AOs) ca on the constituent atoms, and we express this mathematically as follows:
\[\phi_K = \sum_a C_{K,a} \chi_a,\]
where the CK,a are called linear combination of atomic orbital to form molecular orbital (LCAO-MO) coefficients. The MOs are supposed to be solutions to the Schrödinger equation in which the Hamiltonian H involves the kinetic energy of the electron as well as the potentials VL and VR detailing its attraction to the left and right atomic centers (this one-electron Hamiltonian is only an approximation for describing molecular orbitals; more rigorous N-electron treatments will be discussed in Chapter 6):
\[H = - \frac{\hbar^2}{2m} \nabla^2 + V_L + V_R.\]
In contrast, the AOs centered on the left atom A are supposed to be solutions of the Schrödinger equation whose Hamiltonian is H = - \hbar^2/2m \nabla^2 + VL , and the AOs on the right atom B have H = - \hbar^2/2m \nabla^2 + VR. Substituting fK = Sa CK,a ca into the MO’s Schrödinger equation
\[\textbf{H}\phi_K = \varepsilon_K \phi_K\]
and then multiplying on the left by the complex conjugate of \(\chi_b\) and integrating over the \(r\), \(\theta\) and \(\phi\) coordinates of the electron produces
\[\sum_a <\chi_b| - \frac{\hbar^2}{2m} \nabla^2 + V_L + V_R |\chi_a> C_{K,a} = \varepsilon_K \sum_a <\chi_b|\chi_a> C_{K,a}\]
Recall that the Dirac notation <a|b> denotes the integral of a* and b, and <a| op| b> denotes the integral of a* and the operator op acting on b.
In what is known as the Hückel model in chemistry or the tight-binding model in solid-state theory, one approximates the integrals entering into the above set of linear equations as follows:
i. The diagonal integral \(<\chi_b| - \frac{\hbar^2}{2m} \nabla^2 + V_L + V_R |\chi_b>\) involving the AO centered on the right atom and labeled cb is assumed to be equivalent to \(<\chi_b| - \frac{\hbar^2}{2m} \nabla^2 + V_R |\chi_b>\), which means that net attraction of this orbital to the left atomic center is neglected. Moreover, this integral is approximated in terms of the binding energy (denoted \(\alpha\), not to be confused with the electron spin function a) for an electron that occupies the \(\chi_b\) orbital: \(<\chi_b| - \frac{\hbar^2}{2m} \nabla^2 + V_R |\chi_b> = \alpha_b \). The physical meaning of \(\alpha_b\) is the kinetic energy of the electron in \(\chi_b\) plus the attraction of this electron to the right atomic center while it resides in (\chi_b\). Of course, an analogous approximation is made for the diagonal integral involving (\chi_a\); \(<\chi_a| - \frac{\hbar^2}{2m} \nabla^2 + V_L |\chi_a> = \alpha_a \) . These (\alpha\) values are negative quantities because, as is convention in electronic structure theory, energies are measured relative to the energy of the electron when it is removed from the orbital and possesses zero kinetic energy.
ii. The off-diagonal integrals \(<\chi_b| - \frac{\hbar^2}{2m} \nabla^2 + V_L + V_R |\chi_a>\) are expressed in terms of a parameter \(\beta_{a,b}\) which relates to the kinetic and potential energy of the electron while it resides in the “overlap region” in which both \(\chi_a\) and \(\chi_b\) are non-vanishing. This region is shown pictorially above as the region where the left and right orbitals touch or overlap. The magnitude of \(\beta\) is assumed to be proportional to the overlap \(S_{a,b}\) between the two AOs : \(S_{a,b} = <\chi_a|\chi_b>\). It turns out that \(\beta\) is usually a negative quantity, which can be seen by writing it as \(<\chi_b| - \frac{\hbar^2}{2m} \nabla^2 + V_R |\chi_a> + <\chi_b| V_L |\chi_a>\). Since (\chi_a\) is an eigenfunction of \(- \frac{\hbar^2}{2m} \nabla^2 + V_R\) having the eigenvalue \(\alpha_a\), the first term is equal to \(\alpha_a\) (a negative quantity) times \(<\chi_b|\chi_a>\), the overlap \(S\). The second quantity \(<\chi_b| V_L |\chi_a>\) is equal to the integral of the overlap density \(\chi_b(r)\chi_a(r)\) multiplied by the (negative) Coulomb potential for attractive interaction of the electron with the left atomic center. So, whenever \(\chi_b(r)\) and \(\chi_a(r)\) have positive overlap, b will turn out negative.
iii. Finally, in the most elementary Hückel or tight-binding model, the off-diagonal overlap integrals \(<\chi_a|\chi_b>=S_{a,b}\) are neglected and set equal to zero on the right side of the matrix eigenvalue equation. However, in some Hückel models, overlap between neighboring orbitals is explicitly treated, so, in some of the discussion below we will retain \(S_{a,b}\).
With these Hückel approximations, the set of equations that determine the orbital energies \(\varepsilon_K\) and the corresponding LCAO-MO coefficients \(C_{K,a}\) are written for the two-orbital case at hand as in the first 2x^2 matrix equations shown below
which is sometimes written a
These equations reduce with the assumption of zero overlap to
The a parameters are identical if the two AOs ca and cb are identical, as would be the case for bonding between the two 1s orbitals of two H atoms or two 2pp orbitals of two C atoms or two 3s orbitals of two Na atoms. If the left and right orbitals were not identical (e.g., for bonding in HeH+ or for the p bonding in a C-O group), their a values would be different and the Hückel matrix problem would look like:
To find the MO energies that result from combining the AOs, one must find the values of e for which the above equations are valid. Taking the 2x^2 matrix consisting of e times the overlap matrix to the left hand side, the above set of equations reduces to the third set displayed earlier. It is known from matrix algebra that such a set of linear homogeneous equations (i.e., having zeros on the right hand sides) can have non-trivial solutions (i.e., values of \(C\) that are not simply zero) only if the determinant of the matrix on the left side vanishes. Setting this determinant equal to zero gives a quadratic equation in which the e values are the unknowns:
\[(\alpha-\varepsilon)^2 – (\beta - \varepsilon S)^2 = 0.\]
This quadratic equation can be factored into a product
\[(\alpha - \beta - \varepsilon +\varepsilon S) (\alpha + \beta - \varepsilon -\varepsilon S) = 0\]
which has two solutions
\[\varepsilon = \frac{\alpha + \beta}{1 + S}, \text{ and } \varepsilon = \frac{\alpha - \beta}{1 – S}.\]
As discussed earlier, it turns out that the b values are usually negative, so the lowest energy such solution is the \varepsilon = (\alpha + \beta)/(1 + S) solution, which gives the energy of the bonding MO. Notice that the energies of the bonding and anti-bonding MOs are not symmetrically displaced from the value a within this version of the Hückel model that retains orbital overlap. In fact, the bonding orbital lies less than b below a, and the antibonding MO lies more than b above a because of the \(1+S\) and \(1-S\) factors in the respective denominators. This asymmetric lowering and raising of the MOs relative to the energies of the constituent AOs is commonly observed in chemical bonds; that is, the antibonding orbital is more antibonding than the bonding orbital is bonding. This is another important thing to keep in mind because its effects pervade chemical bonding and spectroscopy.
Having noted the effect of inclusion of AO overlap effects in the Hückel model, I should admit that it is far more common to utilize the simplified version of the Hückel model in which the S factors are ignored. In so doing, one obtains patterns of MO orbital energies that do not reflect the asymmetric splitting in bonding and antibonding orbitals noted above. However, this simplified approach is easier to use and offers qualitatively correct MO energy orderings. So, let’s proceed with our discussion of the Hückel model in its simplified version.
To obtain the LCAO-MO coefficients corresponding to the bonding and antibonding MOs, one substitutes the corresponding a values into the linear equations
and solves for the Ca coefficients (actually, one can solve for all but one Ca, and then use normalization of the MO to determine the final Ca). For example, for the bonding MO, we substitute \(\varepsilon = \alpha + \beta\) into the above matrix equation and obtain two equations for \(C_L\) and \(C_R\):
\[- \beta C_L + \beta C_R = 0\]
\[\beta C_L - \beta C_R = 0.\]
These two equations are clearly not independent; either one can be solved for one C in terms of the other C to give:
\[C_L = C_R,\]
which means that the bonding MO is
\[\phi = C_L (\chi_L + \chi_R).\]
The final unknown, C_L, is obtained by noting that f is supposed to be a normalized function \(<\phi|\phi> = 1\). Within this version of the Hückel model, in which the overlap S is neglected, the normalization of f leads to the following condition:
\[1 = <\phi|\phi> = C_\textbf{L}^2 (<\chi_L|\chi_L> + <\chi_R\chi_R>) = 2 C_\textbf{L}^2\]
with the final result depending on assuming that each c is itself also normalized. So, finally, we know that \(C_L = \frac{1}{\sqrt{2}}\), and hence the bonding MO is:
\[\phi = \frac{1}{\sqrt{2}} (\chi_L + \chi_R).\]
Actually, the solution of \(1 = 2 C_\textbf{L}^2\) could also have yielded \(C_L = - \frac{1}{\sqrt{2}}\) and then, we would have
\[\phi = - \frac{1}{\sqrt{2}} (\chi_L + \chi_R).\]
These two solutions are not independent (one is just –1 times the other), so only one should be included in the list of MOs. However, either one is just as good as the other because, as shown very early in this text, all of the physical properties that one computes from a wave function depend not on \(\psi\) but on \(\psi^*\psi\). So, two wave functions that differ from one another by an overall sign factor as we have here have exactly the same \(\psi^*\psi\) and thus are equivalent.
In like fashion, we can substitute \varepsilon = \alpha - \beta into the matrix equation and solve for the \(C_L\) can \(C_R\) values that are appropriate for the antibonding MO. Doing so, gives us:
\[\phi^* = \frac{1}{\sqrt{2}} (\chi_L - \chi_R)\]
or, alternatively,
\[\phi^* = \frac{1}{\sqrt{2}} (\chi_R - \chi_L).\]
Again, the fact that either expression for f* is acceptable shows a property of all solutions to any Schrödinger equations; any multiple of a solution is also a solution. In the above example, the two answers for f* differ by a multiplicative factor of (-1).
Let’s try another example to practice using Hückel or tight-binding theory. In particular, I’d like you to imagine two possible structures for a cluster of three Na atoms (i.e., pretend that someone came to you and asked what geometry you think such a cluster would assume in its ground electronic state), one linear and one an equilateral triangle. Further, assume that the Na-Na distances in both such clusters are equal (i.e., that the person asking for your theoretical help is willing to assume that variations in bond lengths are not the crucial factor in determining which structure is favored). In Fig. 2.11, I shown the two candidate clusters and their 3s orbitals.
Figure 2.11. Linear and equilateral triangle structures of sodium trimer.
Numbering the three Na atoms’ valence 3s orbitals \(\chi_1\), \(\chi_2\), and \(\chi_3\), we then set up the 3x3 Hückel matrix appropriate to the two candidate structures:
for the linear structure (n.b., the zeros arise because \(\chi_1\) and \(\chi_3\) do not overlap and thus have no b coupling matrix element). Alternatively, for the triangular structure, we find
as the Hückel matrix. Each of these 3x3 matrices will have three eigenvalues that we obtain by subtracting e from their diagonals and setting the determinants of the resulting matrices to zero. For the linear case, doing so generates
\[(\alpha-\varepsilon)^3 – 2 \beta^2 (\alpha-\varepsilon\alpha-\varepsilon) = 0,\]
and for the triangle case it produces
\[(\alpha-\varepsilon)^3 –3 \beta^2 (\alpha-\varepsilon) + 2 \alpha-\varepsilon = 0.\]
The first cubic equation has three solutions that give the MO energies:
\[\varepsilon = \alpha + \sqrt{2} \beta, \varepsilon = a, \text{ and } \varepsilon = \alpha - \sqrt{2} \beta,\]
for the bonding, non-bonding and antibonding MOs, respectively. The second cubic equation also has three solutions
\[\varepsilon = \alpha + 2\beta, \varepsilon = \alpha - \beta , \text{ and } \varepsilon = \alpha - \beta.\]
So, for the linear and triangular structures, the MO energy patterns are as shown in Fig. 2.12.
Figure 2.12. Energy orderings of molecular orbitals of linear and triangular sodium trimer.
For the neutral \(Na_3\) cluster about which you were asked, you have three valence electrons to distribute among the lowest available orbitals. In the linear case, we place two electrons into the lowest orbital and one into the second orbital. Doing so produces a 3-electron state with a total energy of \(E= 2(\alpha+21/2 \beta) + \alpha= 3\alpha +2\sqrt{2}\beta\). Alternatively, for the triangular species, we put two electrons into the lowest MO and one into either of the degenerate MOs resulting in a 3-electron state with total energy E = 3 \alpha + 3b. Because b is a negative quantity, the total energy of the triangular structure is lower than that of the linear structure since \(3 > 2\sqrt{2}\).
The above example illustrates how we can use Hückel or tight-binding theory to make qualitative predictions (e.g., which of two shapes is likely to be of lower energy).
Notice that all one needs to know to apply such a model to any set of atomic orbitals that overlap to form MOs is
(i) the individual AO energies a (which relate to the electronegativity of the AOs),
(ii) the degree to which the AOs couple (the b parameters which relate to AO overlaps),
(iii) an assumed geometrical structure whose energy one wants to estimate.
This example and the earlier example pertinent to H2 or the p bond in ethylene also introduce the idea of symmetry. Knowing, for example, that H2, ethylene, and linear Na3 have a left-right plane of symmetry allows us to solve the Hückel problem in terms of symmetry-adapted atomic orbitals rather than in terms of primitive atomic orbitals as we did earlier. For example, for linear Na3, we could use the following symmetry-adapted functions:
\[\chi_2 {\rm and} \frac{1}{\sqrt{2}} (\chi_1 + \chi_3)\]
both of which are even under reflection through the symmetry plane and
\[ \frac{1}{\sqrt{2}} (\chi_1 - \chi_3)\]
which is odd under reflection. The 3x3 Hückel matrix would then have the form
For example, \(H_{1,2}\) and \(H_{2,3}\) are evaluated as follows
\[ H_{1,2} = <\frac{1}{\sqrt{2}} (\chi_1 + \chi_3)|H|\chi_2> = 2\frac{1}{\sqrt{2}} \beta\]
\[H_{2,3} = <\frac{1}{\sqrt{2}} (\chi_1 + \chi_3)|H|<\frac{1}{\sqrt{2}} (\chi_1 - \chi_3)> = \frac{1}{2}( \alpha + \beta - \beta - \alpha)= 0.\]
The three eigenvalues of the above Hückel matrix are easily seen to be \(\alpha\), \(\alpha+\sqrt{2}\beta\) , and \(\alpha-\sqrt{2}\beta\) , exactly as we found earlier. So, it is not necessary to go through the process of forming symmetry-adapted functions; the primitive Hückel matrix will give the correct answers even if you do not. However, using symmetry allows us to break the full (3x3 in this case) Hückel problem into separate Hückel problems for each symmetry component (one odd function and two even functions in this case, so a 1x1 and a 2x^2 sub - matrix).
While we are discussing the issue of symmetry, let me briefly explain the concept of approximate symmetry again using the above Hückel problem as it applies to ethylene as an illustrative example.
Figure 2.12a Ethylene molecule’s p and p* orbitals showing the \(\sigma_{X,Y}\) reflection plane that is a symmetry property of this molecule.
Clearly, as illustrated in Fig. 2.12a, at its equilibrium geometry the ethylene molecule has a plane of symmetry (denoted \(\sigma_{X,Y}\)) that maps nuclei and electrons from its left to its right and vice versa. This is the symmetry element that could used to decompose the 2x^2 Hückel matrix describing the p and p* orbitals into two 1x1 matrices. However, if any of the four C-H bond lengths or HCH angles is displaced from its equilibrium value in a manner that destroys the perfect symmetry of this molecule, or if one of the C-H units were replaced by a C-CH3 unit, it might appear that symmetry would no longer be a useful tool in analyzing the properties of this molecule’s molecular orbitals. Fortunately, this is not the case.
Even if there is not perfect symmetry in the nuclear framework of this molecule, the two atomic pp orbitals will combine to produce a bonding p and antibonding p* orbital. Moreover, these two molecular orbitals will still possess nodal properties similar to those shown in Fig. 2.12a even though they will not possess perfect even and odd character relative to the \(\sigma_{X,Y}\) plane. The bonding orbital will still have the same sign to the left of the \(\sigma_{X,Y}\) plane as it does to the right, and the antibonding orbital will have the opposite sign to the left as it does to the right, but the magnitudes of these two orbitals will not be left-right equal. This is an example of the concept of approximate symmetry. It shows that one can use symmetry, even when it is not perfect, to predict the nodal patterns of molecular orbitals, and it is the nodal patterns that govern the relative energies of orbitals as we have seen time and again.
Let’s see if you can do some of this on your own. Using the above results, would you expect the cation Na3+ to be linear or triangular? What about the anion Na3-? Next, I want you to substitute the MO energies back into the 3x3 matrix and find the \(\chi_1\), \(\chi_2\), and \(\chi_3\) coefficients appropriate to each of the 3 MOs of the linear and of the triangular structure. See if doing so leads you to solutions that can be depicted as shown in Fig. 2.13, and see if you can place each set of MOs in the proper energy ordering.
Figure 2.13. The molecular orbitals of linear and triangular sodium trimer (note, they are not energy ordered in this figure).
Now, I want to show you how to broaden your horizons and use tight-binding theory to describe all of the bonds in a more complicated molecule such as ethylene shown in Fig. 2.14. What is different about this kind of molecule when compared with metallic or conjugated species is that the bonding can be described in terms of several pairs of valence orbitals that couple to form two-center bonding and antibonding molecular orbitals. Within the Hückel model described above, each pair of orbitals that touch or overlap gives rise to a 2x^2 matrix. More correctly, all n of the constituent valence orbitals form an nxn matrix, but this matrix is broken up into 2x^2 \betalocks. Notice that this did not happen in the triangular Na3 case where each AO touched two other AOs. For the ethlyene case, the valence orbitals consist of (a) four equivalent C sp2 orbitals that are directed toward the four H atoms, (b) four H 1s orbitals, (c) two C sp2 orbitals directed toward one another to form the C-C s bond, and (d) two C pp orbitals that will form the C-C p bond. This total of 12 orbitals generates 6 Hückel matrices as shown below the ethylene molecule.
Figure 2.14 Ethylene molecule with four C-H bonds, one C-C s bond, and one C-C p bond.
We obtain one 2x^2 matrix for the C-C s bond of the form
and one 2x^2 matrix for the C-C p bond of the form
Finally, we also obtain four identical 2x^2 matrices for the C-H bonds:
The above matrices produce (a) four identical C-H bonding MOs having energies \(\varepsilon = 1/2 {(\alpha_H + \alpha_C) –\sqrt{(\alpha_H - \alpha_C)^2 + 2\beta^2}}\), (b) four identical C-H antibonding MOs having energies \(\varepsilon^* = 1/2 {(\alpha_H + \alpha_C) + \sqrt{(\alpha_H - \alpha_C)^2 + 2\beta^2}}\), (c) one bonding C-C p orbital with \(\varepsilon = \alpha_{p\pi}+ \beta\) , (d) a partner antibonding C-C orbital with \(\varepsilon^* = \alpha_{p\pi} - \beta\), (e) a C-C s bonding MO with \(\varepsilon = \alpha_{sp2}+ \beta\) , and (\phi) its antibonding partner with \(\varepsilon^* = \alpha_{sp2}- \beta\). In all of these expressions, the \(\beta\) parameter is supposed to be that appropriate to the specific orbitals that overlap as shown in the matrices.
If you wish to practice this exercise of breaking a large molecule down into sets of interacting valence, try to see what Hückel matrices you obtain and what bonding and antibonding MO energies you obtain for the valence orbitals of methane shown in Fig. 2.15.
Figure 2.15. Methane molecule with four C-H bonds.
Before leaving this discussion of the Hückel/tight-binding model, I need to stress that it has its flaws (because it is based on approximations and involves neglecting certain terms in the Schrödinger equation). For example, it predicts (see above) that ethylene has four energetically identical C-H bonding MOs (and four degenerate C-H antibonding MOs). However, this is not what is seen when photoelectron spectra are used to probe the energies of these MOs. Likewise, it suggests that methane has four equivalent C-H bonding and antibonding orbitals, which, again is not true. It turns out that, in each of these two cases (ethylene and methane), the experiments indicate a grouping of four nearly iso-energetic bonding MOs and four nearly iso-energetic antibonding MOs. However, there is some “splitting” among these clusters of four MOs. The splittings can be interpreted, within the Hückel model, as arising from couplings or interactions among, for example, one sp2 or sp3 orbital on a given C atom and another such orbital on the same atom. Such couplings cause the nxn Hückel matrix to not block-partition into groups of 2x^2 su\beta - matrices because now there exist off-diagonal b factors that couple one pair of directed valence to another. When such couplings are included in the analysis, one finds that the clusters of MOs expected to be degenerate are not but are split just as the photoelectron data suggest.
2.5 Hydrogenic Orbitals
The Hydrogenic atom problem forms the basis of much of our thinking about atomic structure. To solve the corresponding Schrödinger equation requires separation of the r, q, and f variables.
The Schrödinger equation for a single particle of mass m moving in a central potential (one that depends only on the radial coordinate r) can be written as
\[-\frac{\hbar^2}{2\mu}\left(\frac{\partial^2}{\partial x^2}+\frac{\partial^2}{\partial y^2}+\frac{\partial^2}{\partial z^2}\right)\psi+V(\sqrt{x^2+y^2+z^2}\Psi=E\psi\]
or, introducing the short-hand notation \(\nabla^2\):
\[-\frac{\hbar^2}{2\mu} \nabla^2 \psi + V \psi = E\psi.\]
This equation is not separable in Cartesian coordinates (x,y,z) because of the way x,y, and z appear together in the square root. However, it is separable in spherical coordinates where it has the form
\[-\frac{\hbar^2}{2\mu r^2} \left(\frac{\partial}{\partial r}\left(r^2\frac{\partial\psi}{\partial r}\right)\right) -\frac{\hbar^2}{2\mu r^2} \frac{1}{\sin\theta}\frac{\partial}{\partial \theta}\left(\sin\theta\frac{\partial \psi}{\partial\theta}\right) -\frac{\hbar^2}{2\mu r^2}\frac{1}{\sin^2\theta}\frac{\partial^2 \psi}{\partial\theta^2}+V(r)\psi=-\frac{\hbar^2}{2\mu r^2}\nabla^2\Psi+V\psi=E\psi.\]
Subtracting V(r) y from both sides of the equation and multiplying by - then moving the derivatives with respect to r to the right-hand side, one obtains
\[ \frac{1}{\sin\theta}\frac{\partial}{\partial \theta} \left(\sin\theta\frac{\partial \psi}{\partial\theta} \right) + \frac{1}{\sin^2\theta}\frac{\partial^2 \psi}{\partial\phi^2}
= -\frac{2\mu r^2}{\hbar^2}(E-V(r)) \psi - \left(\frac{\partial}{\partial r}\left(r^2\frac{\partial\psi}{\partial r}\right)\right).\]
Notice that, except for \(\psi\) itself, the right-hand side of this equation is a function of \(r\) only; it contains no \(\theta\) or \(\phi\) dependence. Let's call the entire right hand side \(\Phi(r) \psi\) to emphasize this fact.
To further separate the q and f dependence, we multiply by Sin2q and subtract the q derivative terms from both sides to obtain
\[\frac{\partial^2 \psi}{\partial\phi^2}= \Phi(r)\psi\sin^2\theta - \sin\theta\frac{\partial}{\partial\theta} \left(\sin\theta\frac{\partial \psi}{\partial\theta} \right).\]
Now we have separated the \(\phi\) dependence from the q and r dependence. We now introduce the procedure used to separate variables in differential equations and assume y can be written as a function of \(\phi\) times a function of \(r\) and \(\theta\): \(\psi = \Phi(\phi) Q(r,\theta)\). Dividing by \(\Phi Q\), we obtain
\[ \frac{1}{\Phi}\frac{\partial^2\Phi}{\partial \phi^2}= \frac{1}{Q}\left(F(r)\sin^2\theta Q-\sin\theta\frac{\partial }{\partial\theta}\left(\sin\theta\frac{\partial Q}{\partial\theta}\right)\right).\]
Now all of the \(\phi\) dependence is isolated on the left hand side; the right hand side contains only \(r\) and \(\theta\) dependence.
Whenever one has isolated the entire dependence on one variable as we have done above for the \(\phi\) dependence, one can easily see that the left and right hand sides of the equation must equal a constant. For the above example, the left hand side contains no \(r\) or \(\theta\) dependence and the right hand side contains no \(\phi\) dependence. Because the two sides are equal for all values of \(r\), \(\theta\), and \(\phi\), they both must actually be independent of \(r\), \(\theta\), and \(\phi\) dependence; that is, they are constant. This again is what is done when one employs the separations of variables method in partial differential equations.
For the above example, we therefore can set both sides equal to a so-called separation constant that we call \(-m^2\). It will become clear shortly why we have chosen to express the constant in the form of minus the square of an integer. You may recall that we studied this same \(\phi\) - equation earlier and learned how the integer m arises via. the boundary condition that \(\phi\) and \(\phi +2\pi\) represent identical geometries.
2.5.1. The \(\Phi\) Equation
The resulting \(\Phi\) equation reads (the “ symbol is used to represent second derivative)
\[\Phi'' + m^2\Phi = 0.\]
This equation should be familiar because it is the equation that we treated much earlier when we discussed z-component of angular momentum. So, its further analysis should also be familiar, but for completeness, I repeat much of it. The above equation has as its most general solution
\[ \Phi = A e^{im\phi} + B e^{-im\phi} .\]
Because the wave functions of quantum mechanics represent probability densities, they must be continuous and single-valued. The latter condition, applied to our F function, means (n.b., we used this in our earlier discussion of z-component of angular momentum) that
\[\Phi(\phi) = \Phi(2\pi+\phi) \] or,
\[Ae^{im\phi}(1-e^{2im\pi})+ Be^{-im\phi}(1-e^{2im\pi})= 0.\]
This condition is satisfied only when the separation constant is equal to an integer \(m = 0, ±1, ± 2, ... \). and provides another example of the rule that quantization comes from the boundary conditions on the wave function. Here m is restricted to certain discrete values because the wave function must be such that when you rotate through 2p about the z-axis, you must get back what you started with.
2.5.2. The Q Equation
Now returning to the equation in which the f dependence was isolated from the r and q dependence and rearranging the q terms to the left-hand side, we have
-\[ \frac{1}{\sin\theta}\frac{\partial }{\partial \theta} \left(\sin\theta\frac{\partial Q}{\partial\theta} \right) - \frac{m^2Q}{\sin^2\theta} = F(r)Q.\]
In this equation we have separated the q and r terms, so we can further decompose the wave function by introducing Q = Q(q) R(r) , which yields
\[ \frac{1}{\Theta\sin\theta}\frac{\partial }{\partial \theta} \left(\sin\theta\frac{\partial \Theta}{\partial\theta} \right) - \frac{m^2}{\sin^2\theta} = \frac{F(r)Q}{R}=-\lambda.\]
where a second separation constant, -l, has been introduced once the r and q dependent terms have been separated onto the right and left hand sides, respectively.
We now can write the q equation as
\[ \frac{1}{\sin\theta}\frac{\partial }{\partial \theta} \left(\sin\theta\frac{\partial \Theta}{\partial\theta} \right) - \frac{m^2\Theta}{\sin^2\theta} = -\lambda\Theta.\]
where m is the integer introduced earlier. To solve this equation for \(\Theta\), we make the substitutions \(z =\cos\theta\) and \(P(z) = \Theta(\theta)\) , so \(\sqrt{1-z^2}=\sin\theta\) , and
\[ \frac{\partial }{\partial \theta} = \frac{\partial z}{\partial \theta}\frac{\partial }{\partial z}= - \(\sin\theta\) \frac{\partial }{\partial z}.\]
The range of values for \(\theta\) was \(0 \le \theta < \pi\) , so the range for \(z\) is \(-1 < z < 1\). The equation for \(\Theta\), when expressed in terms of \(P\) and \(z\), becomes
\[ \frac{d}{dz}\left((1-z^2)\frac{dP}{dz}\right)- \frac{m^2P}{1-z^2}+ \lambda P = 0.\]
Now we can look for polynomial solutions for P, because z is restricted to be less than unity in magnitude. If m = 0, we first let
\[ P = \sum_{k=0}a_kz^k,\]
and substitute into the differential equation to obtain
\[ \sum_{k=0}(k+2)(k+1)a_{k+2}z^k - \sum_{k=0}(k+1)ka_{k}z^k+ \lambda\sum_{k=0}a_kz^k = 0.\]
Equating like powers of z gives
\[ a_{k+2} = \frac{a_k(k(k+1)-\lambda)}{(k+2)(k+1)}.\]
Note that for large values of \(k\)
\[\frac{a_{k+2}}{a_{k}} \rightarrow \frac{k^2\left(1+\frac{1}{k}\right)}{k^2\left(1+\frac{2}{k}\right)\left(1+\frac{1}{k}\right)} = 1.\]
Since the coefficients do not decrease with \(k\) for large \(k\), this series will diverge for \(z = ± 1\) unless it truncates at finite order. This truncation only happens if the separation constant \(\lambda\) obeys \(\lambda = \lambda(\lambda+1)\), where l is an integer (you can see this from the recursion relation giving \(a_{k+2}\) in terms of \(a_k\); only for certain values of l will the numerator vanish ). So, once again, we see that a boundary condition (i.e., that the wave function not diverge and thus be normalizable in this case) give rise to quantization. In this case, the values of l are restricted to \(\lambda(\lambda+1)\); before, we saw that m is restricted to 0, ±1, ± 2, .. .
Since the above recursion relation links every other coefficient, we can choose to solve for the even and odd functions separately. Choosing a0 and then determining all of the even \(a_k\) in terms of this \(a_1\), followed by rescaling all of these \(a_k\) to make the function normalized generates an even solution. Choosing \(a_1\) and determining all of the odd \(a_k\) in like manner, generates an odd solution.
For l= 0, the series truncates after one term and results in \(P_o(z) = 1\). For l= 1 the same thing applies and \(P_1(z) = z\). For l= 2, \(a_2 = -6 \frac{a_o}{2}= -3a_o\), so one obtains \(P_2 = 3z^2-1\), and so on. These polynomials are called Legendre polynomials and are denoted Pl(z).
For the more general case where \(m \ne 0\), one can proceed as above to generate a polynomial solution for the Q function. Doing so, results in the following solutions:
\[P_l^m(z)=(1-z^2)^{|m|/2}\frac{d^{|m|}P_l(z)}{dz^{|m|}}\]
These functions are called Associated Legendre polynomials, and they constitute the solutions to the Q problem for non-zero m values.
The above P and e^{im\phi} functions, when re-expressed in terms of q and f, yield the full angular part of the wave function for any centrosymmetric potential. These solutions are usually written as
\[Y_{l,m}(\theta,\phi)= P_l^m(\cos\theta)\frac{1}{\sqrt{2\pi}} \exp(im\phi),\]
and are called spherical harmonics. They provide the angular solution of the \(r,\theta,\phi\) Schrödinger equation for any problem in which the potential depends only on the radial coordinate. Such situations include all one-electron atoms and ions (e.g., H, He+, Li++, etc.), the rotational motion of a diatomic molecule (where the potential depends only on bond length r), the motion of a nucleon in a spherically symmetrical box (as occurs in the shell model of nuclei), and the scattering of two atoms (where the potential depends only on interatomic distance).
The Yl,m functions possess varying number of angular nodes, which, as noted earlier, give clear signatures of the angular or rotational energy content of the wave function. These angular nodes originate in the oscillatory nature of the Legendre and associated Legendre polynomials Plm (\cos\theta); the higher l is, the more sign changes occur within the polynomial.
2.5.3. The \(R\) Equation
Let us now turn our attention to the radial equation, which is the only place that the explicit form of the potential appears. Using our earlier results for the equation obeyed by the R(r) function and specifying \(V(r)\) to be the Coulomb potential appropriate for an electron in the field of a nucleus of charge +Ze, yields:
\[\frac{1}{r^2}\frac{d}{dr}\left(r^2\frac{dR}{dr}\right)+\left(\frac{2\mu}{\hbar^2}\left(E+\frac{Ze^2}{r}\right)-\frac{L(L+1)}{r^2}\right) R = 0.\]
We can simplify things considerably if we choose rescaled length and energy units because doing so removes the factors that depend on \(\mu\), \(\hbar\) , and \(e\). We introduce a new radial coordinate \(\rho\) and \(a\) quantity \(\sigma\) as follows:
\[\rho=r\sqrt{\frac{-8\mu E}{\hbar^2}} and \sigma = \frac{\mu Ze^2}{\hbar\sqrt{-2\mu E}}.\]
Notice that if \(E\) is negative, as it will be for bound states (i.e., those states with energy below that of a free electron infinitely far from the nucleus and with zero kinetic energy), \(\rho\) and \(\sigma\) are real. On the other hand, if \(E\) is positive, as it will be for states that lie in the continuum, \(\rho\) and \(\sigma\) will be imaginary. These two cases will give rise to qualitatively different behavior in the solutions of the radial equation developed below.
We now define a function \(S\) such that \(S(\rho) = R(r)\) and substitute \(S\) for \(R\) to obtain:
\[\frac{1}{\rho^2}\frac{d}{d\rho}\left(\rho^2\frac{dS}{d\rho}\right) + \left(-\frac{1}{4}-\frac{L(L+1)}{\rho^2}\right) S = 0.\]
The differential operator terms can be recast in several ways using
\[\frac{1}{\rho^2}\frac{d}{d\rho}\left(\rho^2\frac{dS}{d\rho}\right)=\frac{d^2 S}{d\rho^2} +\frac{2}{\rho}\frac{dS}{d\rho} =\frac{1}{\rho}\frac{d^2}{d\rho^2}(\rho S) .\]
The strategy that we now follow is characteristic of solving second order differential equations. We will examine the equation for \(S\) at large and small \(\rho\) values. Having found solutions at these limits, we will use a power series in \(\rho\) to interpolate between these two limits.
Let us begin by examining the solution of the above equation at small values of \(\rho\) to see how the radial functions behave at small \(\rho\). As \(\rho\rightarrow0\), the term \(-L(L+1)/\rho^2\) will dominate over \(-1/4 +\sigma/\rho\). Neglecting these other two terms, we find that, for small values of \(\rho\) (or \(r\)), the solution should behave like \(\rho^L\) and because the function must be normalizable, we must have \(L \ge 0\). Since l can be any non-negative integer, this suggests the following more general form for \(S(r)\):
\[ S(\rho) » \rho^L e^{-a\rho}.\]
This form will insure that the function is normalizable since \(S(r) \rightarrow 0\) as \(r \rightarrow \infty\) for all \(L\), as long as \(\rho\) is a real quantity. If \(\rho\) is imaginary, such a form may not be normalized (see below for further consequences).
Turning now to the behavior of \(S\) for large \(\rho\), we make the substitution of \(S(r)\) into the above equation and keep only the terms with the largest power of \(\rho\) (i.e., the -1/4 term) and we allow the derivatives in the above differential equation to act on \(» \rho^L e^{-a\rho}\). Upon so doing, we obtain the equation
\[ a^2\rho^Le^{-a\rho} = \frac{1}{4}\rho^Le^{-a\rho} ,\]
which leads us to conclude that the exponent in the large-r behavior of S is \(a = \frac{1}{2}\).
Having found the small-\(\rho\) and large-\(\rho\) behaviors of \(S(\rho)\), we can take \(S\) to have the following form to interpolate between large and small r-values:
\[S(\rho) = \rho^Le^{-\frac{\rho}{2}}P(\rho),\]
where the function P is expanded in an infinite power series in \(\rho\) as \(P(\rho) =\sum a_k\rho^k\) . Again substituting this expression for \(S\) into the above equation we obtain
\[P"\rho + P'(2L+2-\rho) + P(\sigma-L-l) = 0,\]
and then substituting the power series expansion of P and solving for the ak's we arrive at a recursion relation for the ak coefficients:
\[a_{k+1} = \frac{(k-\sigma+L+1)a_k}{(k+1)(k+2L+2)}.\]
For large \(k\), the ratio of expansion coefficients reaches the limit \(\frac{a_{k+1}}{a_k}=\frac{1}{k}\) , which, when substituted into \(\sum a_k\rho^k\), gives the same behavior as the power series expansion of \(e^\rho\). Because the power series expansion of \(P\) describes a function that behaves like \(e^\rho\) for large \(\rho\), the resulting \(S(\rho)\) function would not be normalizable because the efactor would be overwhelmed by this \(e^\rho\) dependence. Hence, the series expansion of P must truncate in order to achieve a normalizable \(S\) function. Notice that if \(\rho\) is imaginary, as it will be if E is in the continuum, the argument that the series must truncate to avoid an exponentially diverging function no longer applies. Thus, we see a key difference between bound (with \(\rho\) real) and continuum (with r imaginary) states. In the former case, the boundary condition of non-divergence arises; in the latter, it does not because \(e^{\frac{\rho}{2}\) does not diverge if \(\rho\) is imaginary.
To truncate at a polynomial of order n', we must have \(n' - s + L+ l= 0\). This implies that the quantity s introduced previously is restricted to s = n' + L + l, which is certainly an integer; let us call this integer n. If we label states in order of increasing n = 1,2,3,... , we see that doing so is consistent with specifying a maximum order (n') in the P(r) polynomial n' = 0,1,2,... after which the \textbf{L}_{-}value can run from L = 0, in steps of unity up to L = n-1.
Substituting the integer n for s, we find that the energy levels are quantized because s is quantized (equal to n):
E = -
and the scaled distance turns out to be
r = .
Here, the length ao is the so-called Bohr radius , which turns out to be 0.529 Å; it appears once the above E-expression is substituted into the equation for r. Using the recursion equation to solve for the polynomial's coefficients ak for any choice of n and L quantum numbers generates a so-called Laguerre polynomial; Pn-\textbf{L}_{-}1(r). They contain powers of r from zero through n-\textbf{L}_{-}1, and they have n-\textbf{L}_{-}1 sign changes as the radial coordinate ranges from zero to infinity. It is these sign changes in the Laguerre polynomials that cause the radial parts of the hydrogenic wave functions to have n-\textbf{L}_{-}1 nodes. For example, 3d orbitals have no radial nodes, but 4d orbitals have one; and, as shown in Fig. 2.16, 3p orbitals have one while 3s orbitals have two. Once again, the higher the number of nodes, the higher the energy in the radial direction.
Figure 2.16. Plots of the probability densities r2|R(r)|2 of the radial parts of the 3s and 3p orbitals
Let me again remind you about the danger of trying to understand quantum wave functions or probabilities in terms of classical dynamics. What kind of potential V(r) would give rise to, for example, the 3s P(r) plot shown above? Classical mechanics suggests that P should be large where the particle moves slowly and small where it moves quickly. So, the 3s P(r) plot suggests that the radial speed of the electron has three regions where it is low (i.e., where the peaks in P are) and two regions where it is very large (i.e., where the nodes are). This, in turn, suggests that the radial potential V(r) experienced by the 3s electron is high in three regions (near peaks in P) and low in two regions. Of course, this conclusion about the form of V(r) is nonsense and again illustrates how one must not be drawn into trying to think of the classical motion of the particle, especially for quantum states with small quantum number. In fact, the low quantum number states of such one-electron atoms and ions have their radial P(r) plots focused in regions of r-space where the potential –Ze2/r is most attractive (i.e., largest in magnitude).
Finally, we note that the energy quantization does not arise for states lying in the continuum because the condition that the expansion of P(r) terminate does not arise. The solutions of the radial equation appropriate to these scattering states (which relate to the scattering motion of an electron in the field of a nucleus of charge Z) are a bit outside the scope of this text, so we will not treat them further here. For the interested student, they are treated on p. 90 of the text by Eyring, Walter, and Kimball to which I refer in the Introductory Remarks to this text.
To review, separation of variables has been used to solve the full r,q,f Schrödinger equation for one electron moving about a nucleus of charge Z. The q and f solutions are the spherical harmonics YL,m (\theta,\phi). The bound-state radial solutions
Rn,L(r) = S(r) = rLePn-\textbf{L}_{-}1(r)
depend on the n and L quantum numbers and are given in terms of the Laguerre polynomials.
2.5.4. Summary
To summarize, the quantum numbers L and m arise through boundary conditions requiring that y(q) be normalizable (i.e., not diverge) and y(\phi) = y(f+2p). The radial
equation, which is the only place the potential energy enters, is found to possess both bound-states (i.e., states whose energies lie below the asymptote at which the potential vanishes and the kinetic energy is zero) and continuum states lying energetically above this asymptote. The former states are spatially confined by the potential, but the latter are not. The resulting hydrogenic wave functions (angular and radial) and energies are summarized on pp. 133-136 in the text by L. Pauling and E. B. Wilson for n up to and including 6 and L up to 5 (i.e, for s, p, d, f, g, and h orbitals).
There are both bound and continuum solutions to the radial Schrödinger equation for the attractive coulomb potential because, at energies below the asymptote, the potential confines the particle between r=0 and an outer classical turning point, whereas at energies above the asymptote, the particle is no longer confined by an outer turning point (see Fig. 2.17). This provides yet another example of how quantized states arise when the potential spatially confines the particle, but continuum states arise when the particle is not spatially confined.
Figure 2.17. Radial Potential for Hydrogenic Atoms and Bound and Continuum Orbital Energies.
The solutions of this one-electron problem form the qualitative basis for much of atomic and molecular orbital theory. For this reason, the reader is encouraged to gain a firmer understanding of the nature of the radial and angular parts of these wave functions. The orbitals that result are labeled by n, l, and m quantum numbers for the bound states and by l and m quantum numbers and the energy E for the continuum states. Much as the particle-in-a-box orbitals are used to qualitatively describe p- electrons in conjugated polyenes, these so-called hydrogen-like orbitals provide qualitative descriptions of orbitals of atoms with more than a single electron. By introducing the concept of screening as a way to represent the repulsive interactions among the electrons of an atom, an effective nuclear charge Zeff can be used in place of Z in the yn,l,m and En to generate approximate atomic orbitals to be filled by electrons in a many-electron atom. For example, in the crudest approximation of a carbon atom, the two 1s electrons experience the full nuclear attraction so Zef\phi = 6 for them, whereas the 2s and 2p electrons are screened by the two 1s electrons, so Zef\phi = 4 for them. Within this approximation, one then occupies two 1s orbitals with Z = 6, two 2s orbitals with Z = 4 and two 2p orbitals with Z=4 in forming the full six-electron wave function of the lowest-energy state of carbon. It should be noted that the use of screened nuclear charges as just discussed is different from the use of a quantum defect parameter d as discussed regarding Rydberg orbitals in Chapter 1. The Z = 4 screened charge for carbon’s 2s and 2p orbitals is attempting to represent the effect of the inner-shell 1s electrons on the 2s and 2p orbitals. The modification of the principal quantum number made by replacing n by (n- d) represents the penetration of the orbital with nominal quantum number n inside its inner-shells.
2.6. Electron Tunneling
Tunneling is a phenomenon of quantum mechanics, not classical mechanics. It is an extremely important subject that occurs in a wide variety of chemical species including nano-scale electronic devices and protons moving through water.
As we have seen several times already, solutions to the Schrödinger equation display several properties that are very different from what one experiences in Newtonian dynamics. One of the most unusual and important is that the particles one describes using quantum mechanics can move into regions of space where they would not be allowed to go if they obeyed classical equations. We call these classically forbidden regions. Let us consider an example to illustrate this so-called tunneling phenomenon. Specifically, we think of an electron (a particle that we likely would use quantum mechanics to describe) moving in a direction we will call R under the influence of a potential that is:
a. Infinite for R < 0 (this could, for example, represent a region of space within a solid material where the electron experiences very repulsive interactions with other electrons);
b. Constant and negative for some range of R between R = 0 and Rmax (this could represent the attractive interaction of the electrons with those atoms or molecules in a finite region or surface of a solid);
c. Constant and repulsive (i.e., positive) by an amount dV + De for another finite region from Rmax to Rmax +d (this could represent the repulsive interactions between the electrons and a layer of molecules of thickness d lying on the surface of the solid at Rmax);
d. Constant and equal to De from Rmaz +d to infinity (this could represent the electron being removed from the solid, but with a work function energy cost of De, and moving freely in the vacuum above the surface and the ad-layer). Such a potential is shown in Fig. 2.18.
Figure 2.18. One-dimensional potential showing a well, a barrier, and the asymptotic region.
The piecewise nature of this potential allows the one-dimensional Schrödinger equation to be solved analytically. For energies lying in the range De < E < De +dV, an especially interesting class of solutions exists. These so-called resonance states occur at energies that are determined by the condition that the amplitude of the wave function within the barrier (i.e., for 0 £ R £ Rmax ) be large. Let us now turn our attention to this specific
energy regime, which also serves to introduce the tunneling phenomenon.
The piecewise solutions to the Schrödinger equation appropriate to the resonance case are easily written down in terms of sin and cos or exponential functions, using the following three definitions:
The combination of sin(kR) and cos(kR) that solve the Schrödinger equation in the inner region and that vanish at R=0 (because the function must vanish within the region where V is infinite and because it must be continuous, it must vanish at R=0) is:
y = Asin(kR) (for 0 £ R £ Rmax ).
Between Rmax and Rmax +d, there are two solutions that obey the Schrödiger equation, so the most general solution is a combination of these two:
y = B+ \exp(k'R) + B- \exp(-k'R) (for Rmax £ R £ Rmax +d).
Finally, in the region beyond Rmax + d, we can use a combination of either sin(k’R) and cos(k’R) or \exp(ik’R) and \exp(-ik’R) to express the solution. Unlike the region near R=0, where it was most convenient to use the sin and cos functions because one of them could be “thrown away” since it could not meet the boundary condition of vanishing at R=0, in this large-R region, either set is acceptable. We choose to use the \exp(ik’R) and
exp(-ik’R) set because each of these functions is an eigenfunction of the momentum operator –ih∂/∂R. This allows us to discuss amplitudes for electrons moving with positive momentum and with negative momentum. So, in this region, the most general solution is
y = C \exp(ik'R) + D \exp(-ik'R) (for Rmax +d £ R < \infty).
There are four amplitudes (A, B+, B-, and C) that can be expressed in terms of the specified amplitude D of the incoming flux (e.g., pretend that we know the flux of electrons that our experimental apparatus shoots at the surface). Four equations that can be used to achieve this goal result when y and dy/dR are matched at Rmax and at Rmax + d (one of the essential properties of solutions to the Schrödinger equation is that they and their first derivative are continuous; these properties relate to y being a probability and the momentum –ih∂/∂R being continuous). These four equations are:
Asin(kRmax) = B+ \exp(k'Rmax) + B- \exp(-k'Rmax),
Akcos(kRmax) = k'B+ \exp(k'Rmax) - k'B- \exp(-k'Rmax),
B+ \exp(k'(Rmax + d)) + B- \exp(-k'(Rmax + d))
= C \exp(ik'(Rmax + d) + D \exp(-ik'(Rmax + d),
k'B+ \exp(k'(Rmax + d)) - k'B- \exp(-k'(Rmax + d))
= ik'C \exp(ik'(Rmax + d)) -ik' D \exp(-ik'(Rmax + d)).
It is especially instructive to consider the value of A/D that results from solving this set of four equations in four unknowns because the modulus of this ratio provides information about the relative amount of amplitude that exists inside the barrier in the attractive region of the potential compared to that existing in the asymptotic region as incoming flux.
The result of solving for A/D is:
A/D = 4 k'exp(-ik'(Rmax+d))
{exp(k'd)(ik'-k')(k'sin(kRmax)+kcos(kRmax))/ik'
+ \exp(-k'd)(ik'+k')(k'sin(kRmax)-kcos(kRmax))/ik' }-1.
To simplify this result in a manner that focuses on conditions where tunneling plays a key role in creating the resonance states, it is instructive to consider this result under conditions of a high (large De + dV - E) and thick (large d) barrier. In such a case, the factor \exp(-k'd) will be very small compared to its counterpart \exp(k'd), and so
A/D = 4 \exp(-ik'(Rmax+d)) \exp(-k'd) {k'sin(kRmax)+kcos(kRmax) }-1.
The \exp(-k'd) factor in A/D causes the magnitude of the wave function inside the barrier to be small in most circumstances; we say that incident flux must tunnel through the barrier to reach the inner region and that \exp(-k'd) governs the probability of this tunneling.
Keep in mind that, in the energy range we are considering (E < De+d), a classical particle could not even enter the region Rmax < R < Rmax + d; this is why we call this the classically forbidden or tunneling region. A classical particle starting in the large-R region can not enter, let alone penetrate, this region, so such a particle could never end up in the 0 <R < Rmax inner region. Likewise, a classical particle that begins in the inner region can never penetrate the tunneling region and escape into the large-R region. Were it not for the fact that electrons obey a Schrödinger equation rather than Newtonian dynamics, tunneling would not occur and, for example, scanning tunneling microscopy (STM), which has proven to be a wonderful and powerful tool for imaging molecules on and near surfaces, would not exist. Likewise, many of the devices that appear in our modern electronic tools and games, which depend on currents induced by tunneling through various junctions, would not be available. But, or course, tunneling does occur and it can have remarkable effects.
Let us examine an especially important (in chemistry) phenomenon that takes place because of tunneling and that occurs when the energy E assumes very special values. The magnitude of the A/D factor in the above solutions of the Schrödinger equation can become large if the energy E is such that the denominator in the above expression for A/D approaches zero. This happens when
k'sin(kRmax)+kcos(kRmax)
or if
tan(kRmax) = - k/k’.
It can be shown that the above condition is similar to the energy quantization condition
tan(kRmax) = - k/k
that arises when bound states of a finite potential well similar to that shown above but with the barrier between Rmax and Rmax + d missing and with E below De. There is, however, a difference. In the bound-state situation, two energy-related parameters occur
k =
and
k = .
In the case we are now considering, k is the same, but
k' = )
rather than k occurs, so the two equations involving tan(kRmax) are not identical, but they are quite similar.
Another observation that is useful to make about the situations in which A/D becomes very large can be made by considering the case of a very high barrier (so that k' is much larger than k). In this case, the denominator that appears in A/D
k'sin(kRmax)+kcos(kRmax) @ k' sin(kRmax)
can become small at energies satisfying
sin(kRmax) @ 0.
This condition is nothing but the energy quantization condition that occurs for the particle-in-a-box potential shown in Fig. 2.19.
Figure 2.19. One-dimensional potential similar to the tunneling potential but without the barrier and asymptotic region.
This potential is identical to the potential that we were examining for 0 £ R £ Rmax , but extends to infinity beyond Rmax ; the barrier and the dissociation asymptote displayed by our potential are absent.
Let’s consider what this tunneling problem\hbaras taught us. First, it showed us that quantum particles penetrate into classically forbidden regions. It showed that, at certain so-called resonance energies, tunneling is much more likely than at energies that are off-resonance. In our model problem, this means that electrons impinging on the surface with resonance kinetic energies will have a very high probability of tunneling to produce an electron that is highly localized (i.e., trapped) in the 0 < R < Rmax region. Likewise, it means that an electron prepared (e.g., perhaps by photo-excitation from a lower-energy electronic state) within the 0 < R < Rmax region will remain trapped in this region for a long time (i.e., will have a low probability of tunneling outward).
In the case just mentioned, it would make sense to solve the four equations for the amplitude C of the outgoing wave in the R > Rmax region in terms of the A amplitude. If we were to solve for C/A and then examine under what conditions the amplitude of this ratio would become small (so the electron cannot escape), we would find the same tan(kRmax) = - k/k' resonance condition as we found from the other point of view. This means that the resonance energies tell us for what collision energies the electron will tunnel inward and produce a trapped electron and, at these same energies, an electron that is trapped will not escape quickly.
Whenever one has a barrier on a potential energy surface, at energies above the dissociation asymptote De but below the top of the barrier (De + dV here), one can expect resonance states to occur at special scattering energies E. As we illustrated with the model problem, these so-called resonance energies can often be approximated by the bound-state energies of a potential that is identical to the potential of interest in the inner region (0 £ R £ Rmax ) but that extends to infinity beyond the top of the barrier (i.e., beyond the barrier, it does not fall back to values below E).
The chemical significance of resonances is great. Highly rotationally excited molecules may have more than enough total energy to dissociate (De), but this energy may be stored in the rotational motion, and the vibrational energy may be less than De. In terms of the above model, high rotational angular momentum may produce a significant centrifugal barrier in the effective potential that characterizes the molecule’s vibration, but the system's vibrational energy may lie significantly below De. In such a case, and when viewed in terms of motion on an angular-momentum-modified effective potential such as I show in Fig. 2.20 , the lifetime of the molecule with respect to dissociation is determined by the rate of tunneling through the barrier.
Figure 2.20. Radial potential for non-rotating (J = 0) molecule and for rotating molecule.
In this case, one speaks of rotational predissociation of the molecule. The lifetime t can be estimated by computing the frequency n at which flux that exists inside Rmax strikes the barrier at Rmax
n = (sec-1)
and then multiplying by the probability P that flux tunnels through the barrier from Rmax to Rmax + d:
P = \exp(-2k'd).
The result is that
t -1= \exp(-2k'd)
with the energy E entering into k and k' being determined by the resonance condition: (k'sin(kRmax)+kcos(kRmax)) = minimum. We note that the probability of tunneling \exp(-2k'd) falls of exponentially with a factor depending on the width d of the barrier through which the particle must tunnel multiplied by k’, which depends on the height of the barrier De + d above the energy E available. This exponential dependence on thickness and height of the barriers is something you should keep in mind because it appears in all tunneling rate expressions.
Another important case in which tunneling occurs is in electronically metastable states of anions. In so-called shape resonance states, the anion’s extra electron experiences
an attractive potential due to its interaction with the underlying neutral molecule’s dipole, quadrupole, and induced electrostatic moments, as well as
a centrifugal potential of the form L(L+1)h2/8p2meR2 whose magnitude depends on the angular character of the orbital the extra electron occupies.
When combined, the above attractive and centrifugal potentials produce an effective radial potential of the form shown in Fig. 2.21 for the N2- case in which the added electron occupies the p* orbital which has L=2 character when viewed from the center of the N-N bond. Again, tunneling through the barrier in this potential determines the lifetimes of such shape resonance states.
Figure 2.21 Effective radial potential for the excess electron in N2- occupying the p* orbital which has a dominant L = 2 component.
Although the examples treated above analytically involved piecewise constant potentials (so the Schrödinger equation and the boundary matching conditions could be solved exactly), many of the characteristics observed carry over to more chemically realistic situations. In fact, one can often model chemical reaction processes in terms of motion along a reaction coordinate (s) from a region characteristic of reactant materials where the potential surface is positively curved in all direction and all forces (i.e., gradients of the potential along all internal coordinates) vanish; to a transition state at which the potential surface's curvature along s is negative while all other curvatures are positive and all forces vanish; onward to product materials where again all curvatures are positive and all forces vanish. A prototypical trace of the energy variation along such a reaction coordinate is in Fig. 2.22.
Figure 2.22. Energy profile along a reaction path showing the barrier through which tunneling may occur.
Near the transition state at the top of the barrier on this surface, tunneling through the barrier plays an important role if the masses of the particles moving in this region are sufficiently light. Specifically, if H or D atoms are involved in the bond breaking and forming in this region of the energy surface, tunneling must usually be considered in treating the dynamics.
Within the above reaction path point of view, motion transverse to the reaction coordinate is often modeled in terms of local harmonic motion although more sophisticated treatments of the dynamics is possible. This picture leads one to consider motion along a single degree of freedom, with respect to which much of the above treatment can be carried over, coupled to transverse motion along all other internal degrees of freedom taking place under an entirely positively curved potential (which therefore produces restoring forces to movement away from the streambed traced out by the reaction path). This point of view constitutes one of the most widely used and successful models of molecular reaction dynamics and is treated in more detail in Chapters 3 and 8 of this text.
2.7. Angular Momentum
2.7.1. Orbital Angular Momentum
A particle moving with momentum p at a position r relative to some coordinate origin has so-called orbital angular momentum equal to \(\textbf{L} = \textbf{r} \times \textbf{p}\) . The three components of this angular momentum vector in a Cartesian coordinate system located at the origin mentioned above are given in terms of the Cartesian coordinates of \(\textbf{r}\) and \(\textbf{p}\) as follows:
\[{L}_z = x p_y - y p_x ,\]
\[{L}_x = y p_z - z p_y ,\]
\[{L}_y = z p_x - x p_z .\]
Using the fundamental commutation relations among the Cartesian coordinates and the Cartesian momenta:
\[[ q_k , p_j ] = q_k p_j - p_j q_k = ih \delta_{j,k} ( j,k = x,y,z) ,\]
which are proven by considering quantities of the from
\[(x p_x - p_x x)f=-ih\left[x\frac{\partial f}{\partial x}-\frac{\partial (xf)}{\partial x}\right]=ihf\],
it can be shown that the above angular momentum operators obey the following set of commutation relations:
\[[\textbf{L}_x, \textbf{L}_y] = ih \textbf{L}_z ,\]
\[[\textbf{L}_y, \textbf{L}_z] = ih \textbf{L}_x ,\]
\[[\textbf{L}_z, \textbf{L}_x] = ih \textbf{L}_y .\]
Although the components of L do not commute with one another, they can be shown to commute with the operator \(\textbf{L}^2\) defined by
\[\textbf{L}^2 = \textbf{L}_x^2 + \textbf{L}_y^2 + \textbf{L}_z^2 .\]
This new operator is referred to as the square of the total angular momentum operator.
The commutation properties of the components of L allow us to conclude that complete sets of functions can be found that are eigenfunctions of \(\textbf{L}^2\) and of one, but not more than one, component of L. It is convention to select this one component as \(\textbf{L}_z\), and to label the resulting simultaneous eigenstates of \(\textbf{L}^2\) and \(\textbf{L}_z\) as \(|l,m>\) according to the corresponding eigenvalues:
\[\textbf{L}^2 |l,m> = \hbar^2 l(l+1) |l,m>, l = 0,1,2,3,....\]
\[\textbf{L}_z |l,m> = h m |l,m>, m = ± l, ±(l-1), ±(l-2), ... ±(l-(l-1)), 0.\]
These eigenfunctions of \(\textbf{L}^2\) and of \(\textbf{L}_z\) will not, in general, be eigenfunctions of either \(\textbf{L}_x\) or of \(\textbf{L}_y\). This means that any measurement of \(\textbf{L}_x\) or \(\textbf{L}_y\) will necessarily change the wave function if it begins as an eigenfunction of \(\textbf{L}_z\).
The above expressions for \(\textbf{L}_x\), \(\textbf{L}_y\), and \(\textbf{L}_z\) can be mapped into quantum mechanical operators by substituting \(x\), \(y\), and \(z\) as the corresponding coordinate operators and \(-ih\partial /\partial x\), \(-ih\partial /\partial y\), and \(-ih\partial /\partial z\) for \(p_x\) , \(p_y\) , and \(p_z\) , respectively. The resulting operators can then be transformed into spherical coordinates the results of which are:
\[\textbf{L}_z =-ih \partial /\partial \phi ,\]
\[\textbf{L}_x = ih {\sin\phi \partial /\partial \theta + \cot\theta \cos\phi \partial /\partial \phi} ,\]
\[\textbf{L}_y = -ih {\cos\phi \partial /\partial \theta - \cot\theta \sin\phi \partial /\partial \phi} ,\]
\[\textbf{L}^2 = - \hbar^2 {(1/\sin\theta) \partial /\partial \theta (\sin\theta \partial /\partial \theta) + (1/\sin^2\theta) \partial 2/\partial \phi2} .\]
2.7.2. Properties of General Angular Momenta
There are many types of angular momenta that one encounters in chemistry. Orbital angular momenta, such as that introduced above, arise in electronic motion in atoms, in atom-atom and electron-atom collisions, and in rotational motion in molecules. Intrinsic spin angular momentum is present in electrons, H^1, H^2, C^13, and many other nuclei. In this Section, we will deal with the behavior of any and all angular momenta and their corresponding eigenfunctions.
At times, an atom or molecule contains more than one type of angular momentum. The Hamiltonian's interaction potentials present in a particular species may or may not cause these individual angular momenta to be coupled to an appreciable extent (i.e., the Hamiltonian may or may not contain terms that refer simultaneously to two or more of these angular momenta). For example, the NH- ion, which has a 2P ground electronic state (its electronic configuration is 1sN22s23s22ppx^22ppy1) has electronic spin, electronic orbital, and molecular rotational angular momenta. The full Hamiltonian H contains terms that couple the electronic spin and orbital angular momenta, thereby causing them individually to not commute with H.
In such cases, the eigenstates of the system can be labeled rigorously only by angular momentum quantum numbers j and m belonging to the total angular momentum operators \(\textbf{J}^2\) and \(\textbf{J}_z\). The total angular momentum of a collection of individual angular momenta is defined, component-by-component, as follows:
\[J_k = \sum_i J_k(i),\]
where \(k\) labels \(x\), \(y\), and \(z\), and i labels the constituents whose angular momenta couple to produce J.
For the remainder of this Section, we will study eigenfunction-eigenvalue relationships that are characteristic of all angular momenta and which are consequences of the commutation relations among the angular momentum vector's three components. We will also study how one combines eigenfunctions of two or more angular momenta {J(i)} to produce eigenfunctions of the total J.
a. Consequences of the Commutation Relations
Any set of three operators that obey
\[[\textbf{J}_x, \textbf{J}_y] = i\hbar \textbf{J}_z ,\]
\[[\textbf{J}_y, \textbf{J}_z] = i\hbar \textbf{J}_x ,\]
\[[\textbf{J}_z, \textbf{J}_x] = i\hbar \textbf{J}_y ,\]
will be taken to define an angular momentum J, whose square \(\textbf{J}^2= \textbf{J}_x^2 + \textbf{J}_y^2 + \textbf{J}_z^2\) commutes with all three of its components. It is useful to also introduce two combinations of the three fundamental operators \(\textbf{J}_x\) and \(\textbf{J}_y\):
\[\textbf{J}_{\pm} = \textbf{J}_x ± i \textbf{J}_y ,\]
and to refer to them as raising and lowering operators for reasons that will be made clear below. These new operators can be shown to obey the following commutation relations:
\[[\textbf{J}^2, \textbf{J}_{\pm}] = 0,\]
\[[\textbf{J}_z, \textbf{J}_{\pm}] = \pm \hbar \textbf{J}_{\pm} .\]
Using only the above commutation properties, it is possible to prove important properties of the eigenfunctions and eigenvalues of \textbf{J}^2 and \textbf{J}_z. Let us assume that we have found a set of simultaneous eigenfunctions of \textbf{J}^2 and \textbf{J}_z ; the fact that these two operators commute tells us that this is possible. Let us label the eigenvalues belonging to these functions:
\[\textbf{J}^2 |j,m> = \hbar^2 f(j,m) |j,m>,\]
\[\textbf{J}_z |j,m> = h m |j,m>,\]
in terms of the quantities m and \(f(j,m)\). Although we certainly hint that these quantities must be related to certain j and m quantum numbers, we have not yet proven this, although we will soon do so. For now, we view \(f(j,m)\) and m simply as symbols that represent the respective eigenvalues. Because both \(\textbf{J}^2\) and \(\textbf{J}_z\) are Hermitian, eigenfunctions belonging to different \(f(j,m)\) or m quantum numbers must be orthogonal:
\[<j,m|j',m'> = \delta_{m,m^\prime} \delta_{j,j^\prime} .\]
We now prove several identities that are needed to discover the information about the eigenvalues and eigenfunctions of general angular momenta that we are after. Later in this Section, the essential results are summarized.
i. There is a Maximum and a Minimum Eigenvalue for \(\textbf{J}_z\)
Because all of the components of J are Hermitian, and because the scalar product of any function with itself is positive semi-definite, the following identity holds:
\[<j,m|\textbf{J}_x^2 + \textbf{J}_y^2|j,m> = <\textbf{J}_x<j,m| \textbf{J}_x|j,m> + <\textbf{J}_y<j,m| \textbf{J}_y|j,m> \ge 0.\]
However, \(\textbf{J}_x^2 + \textbf{J}_y^2\) is equal to \(\textbf{J}^2 - \textbf{J}_z^2\), so this inequality implies that
\[<j,m| \textbf{J}^2 - \textbf{J}_z^2 |j,m> = \hbar^2 {f(j,m) - m2} \ge 0,\]
which, in turn, implies that m2 must be less than or equal to \(f(j,m)\). Hence, for any value of the total angular momentum eigenvalue f, the z-projection eigenvalue (m) must have a maximum and a minimum value and both of these must be less than or equal to the total angular momentum squared eigenvalue f.
ii. The Raising and Lowering Operators Change the \(textbf{J}_z\) Eigenvalue but not the \(\textbf{J}^2\) Eigenvalue When Acting on \(|j,m>\)
Applying the commutation relations obeyed by \(\textbf{J}_{\pm}\) to \(|j,m>\) yields another useful result:
\[\textbf{J}_z \textbf{J}_{\pm} |j,m> - \textbf{J}_{\pm} \textbf{J}_z |j,m> = \pm \hbar \textbf{J}_{\pm} |j,m>,\]
\[\textbf{J}^2 \textbf{J}_{\pm} |j,m> - \textbf{J}_{\pm} \textbf{J}^2 |j,m> = 0.\]
Now, using the fact that (|j,m>\) is an eigenstate of \(\textbf{J}^2\) and of \(\textbf{J}_z\), these identities give
\[\textbf{J}_z \textbf{J}_{\pm} |j,m> = (m\hbar \pm \hbar) \textbf{J}_{\pm} |j,m> = h (m±1) |j,m>,\]
\[\textbf{J}^2 \textbf{J}_{\pm} |j,m> = \hbar^2 f(j,m) \textbf{J}_{\pm} |j,m>.\]
These equations prove that the functions \(\textbf{J}_{\pm} |j,m>\) must either themselves be eigenfunctions of \(\textbf{J}^2\) and \(\textbf{J}_z\), with eigenvalues \(\hbar^2 f(j,m)\) and \(\hbar (m+1)\), respectively, or \(\textbf{J}_{\pm} |j,m>\) must equal zero. In the former case, we see that \(\textbf{J}_{\pm}\) acting on \(|j,m>\) generates a new eigenstate with the same \(\textbf{J}^2\) eigenvalue as \(|j,m> \)but with one unit of h higher or lower in \(\textbf{J}_z\) eigenvalue. It is for this reason that we call \(\textbf{J}_{\pm}\) raising and lowering operators. Notice that, although \(\textbf{J}_{\pm} |j,m>\) is indeed an eigenfunction of \(\textbf{J}_z\) with eigenvalue \((m±1) \hbar\), \(\textbf{J}_{\pm} |j,m>\) is not identical to \(|j,m±1>\); it is only proportional to \(|j,m±1>\):
\[\textbf{J}_{\pm} |j,m> = C±j,m |j,m±1>.\]
Explicit expressions for these C±j,m coefficients will be obtained below. Notice also that because the \(\textbf{J}_{\pm} |j,m>\), and hence \(|j,m±1>\), have the same \(\textbf{J}^2\) eigenvalue as \(|j,m>\) (in fact, sequential application of \(\textbf{J}_{\pm}\) can be used to show that all \(|j,m'>\), for all \(m'\), have this same \(\textbf{J}^2\) eigenvalue), the \(\textbf{J}^2\) eigenvalue \(f(j,m)\) must be independent of m. For this reason, \(f\) can be labeled by one quantum number j.
iii. The \textbf{J}^2 Eigenvalues are Related to the Maximum and Minimum \(\textbf{J}_z\) Eigenvalues, Which are Related to One Another
Earlier, we showed that there exists a maximum and a minimum value for m, for any given total angular momentum. It is when one reaches these limiting cases that \(\textbf{J}_{\pm} |j,m> = 0\) applies. In particular,
\[\textbf{J}_{+} |j,m_{\rm max}> = 0,\]
\[\textbf{J}_{-} |j,m_{\rm min}> = 0.\]
Applying the following identities:
\[\textbf{J}_{-} \textbf{J}_{+} = \textbf{J}^2 - \textbf{J}_z^2 -\hbar \textbf{J}_z ,\]
\[\textbf{J}_{+} \textbf{J}_{-} = \textbf{J}^2 - \textbf{J}_z^2 +\hbar \textbf{J}_z,\]
respectively, to \(|j,m_{\rm max}>\) and \(|j,m_{\rm min}>\) gives
\[\hbar^2 \{ f(j,m_{\rm max}) - m_{\rm max}^2 - m_{\rm max}\} = 0,\]
\[\hbar^2 \{ f(j,m_{\rm min}) - m_{\rm min}2 + m_{\rm min}\} = 0,\]
which immediately gives the \(\textbf{J}^2\) eigenvalue \(f(j,m_{\rm max})\) and \(f(j,m_{\rm min})\) in terms of \(m_{\rm max}\) or \(m_{\rm min}\):
\[f(j,m_{\rm max}) = m_{\rm max} (m_{\rm max}+1),\]
\[f(j,m_{\rm min}) = m_{\rm min} (m_{\rm min}-1).\]
So, we now know the \(\textbf{J}^2\) eigenvalues for \(|j,m_{\rm max}>\) and \(|j,m_{\rm min}>\). However, we earlier showed that \(|j,m> \)and \(|j,m-1>\) have the same \(\textbf{J}^2\) eigenvalue (when we treated the effect of \(\textbf{J}_{\pm}\) on \(|j,m>\)) and that the \(\textbf{J}^2\) eigenvalue is independent of m. If we therefore define the quantum number \(j\) to be \(m_{\rm max}\) , we see that the \(\textbf{J}^2\) eigenvalues are given by
\[\textbf{J}^2 |j,m> = \hbar^2 j(j+1) |j,m>.\]
We also see that
\[f(j,m) = j(j+1) = m_{\rm max} (m_{\rm max}+1) = m_{\rm min} (m_{\rm min}-1),\]
from which it follows that
\[m_{\rm min} = - m_{\rm max} .\]
iv. The \(j\) Quantum Number Can Be Integer or Half-Integer
The fact that the m-values run from \(j\) to \(-j\) in unit steps (because of the property of the \(\textbf{J}_{\pm}\) operators), there clearly can be only integer or half-integer values for \(j\). In the former case, the m quantum number runs over \(-j, -j+1, -j+2, ..., -j+(j-1), 0, 1, 2, ... j\);
in the latter, m runs over \(-j, -j+1, -j+2, ...-j+(j-1/2), 1/2, 3/2, ...j\). Only integer and half-integer values can range from \(j\) to \(-j\) in steps of unity. Species whose intrinsic angular momenta are integers are known as Bosons and those with half-integer spin are called Fermions.
v. More on \(\textbf{J}_{\pm} |j,m>\)
Using the above results for the effect of \(\textbf{J}_{\pm}\) acting on \(|j,m>\) and the fact that \(\textbf{J}_{+}\) and \(\textbf{J}_{-}\) are adjoints of one another (two operators \(\textbf{F}\) and \(\textbf{G}\) are adjoints if \(<\psi|\textbf{F}|\chi> = <\textbf{G}\psi|\chi>\), for all \(\psi\) and all \(\chi\)) allows us to write:
\[<j,m| \textbf{J}_{-} \textbf{J}_{+} |j,m> = <j,m| (\textbf{J}^2 - \textbf{J}_z^2 -\hbar \textbf{J}_z ) |j,m>\]
\[= \hbar^2 {j(j+1)-m(m+1)} = <\textbf{J}_{+}<j,m| \textbf{J}_{+}|j,m> = (C+j,m)2,\]
where C+j,m is the proportionality constant between \textbf{J}_{+}|j,m> and the normalized function
|j,m+1>. Likewise, the effect of \textbf{J}_{-} can be expressed as
\[<j,m| \textbf{J}_{+} \textbf{J}_{-} |j,m> = <j,m| (\textbf{J}^2 - \textbf{J}_z^2 +\hbar \textbf{J}_z) |j,m>\]
\[= \hbar^2 {j(j+1)-m(m-1)} = <\textbf{J}_{-}<j,m| \textbf{J}_{-}|j,m> = (C-j,m)2,\]
where C-j,m is the proportionality constant between \textbf{J}_{-} |j,m> and the normalized |j,m-1>. Thus, we can solve for C±j,m after which the effect of \textbf{J}_{\pm} on |j,m> is given by:
\[\textbf{J}_{\pm} |j,m> = h {j(j+1) –m(m±1)}1/2 |j,m±1>.\]
2.7.3. Summary
The above results apply to any angular momentum operators. The essential findings can be summarized as follows:
(i) \(\textbf{J}^2\) and \(\textbf{J}_z\) have complete sets of simultaneous eigenfunctions. We label these eigenfunctions \(|j,m>\); they are orthonormal in both their m- and j-type indices:
\[<j,m| j',m'> = \delta_{m,m^\prime} \delta_{j,j^\prime} .\]
(ii) These \(|j,m>\) eigenfunctions obey:
\[\textbf{J}^2 |j,m> = \hbar^2 j(j+1) |j,m>, \{ j= \text{ integer or half-integer}\},\]
\[\textbf{J}_z |j,m> = h m |j,m>, \{ m = -j,\text{ in steps of 1 to }+j\}.\]
(iii) The raising and lowering operators \(\textbf{J}_{\pm}\) act on \(|j,m>\) to yield functions that are eigenfunctions of \(\textbf{J}^2\) with the same eigenvalue as \(|j,m>\) and eigenfunctions of \(\textbf{J}_z\) with eigenvalue of \((m±1) \hbar\) :
\[\textbf{J}_{\pm} |j,m> = \hbar {j(j+1) - m(m±1)}1/2 |j,m±1>.\]
(iv) When \(\textbf{J}_{\pm}\) acts on the extremal states \(|j,j>\) or \(|j,-j>\), respectively, the result is zero.
The results given above are, as stated, general. Any and all angular momenta have quantum mechanical operators that obey these equations. It is convention to designate specific kinds of angular momenta by specific letters; however, it should be kept in mind that no matter what letters are used, there are operators corresponding to \(\textbf{J}^2\), \(\textbf{J}^z\), and \textbf{J}_{\pm} that obey relations as specified above, and there are eigenfunctions and eigenvalues that have all of the properties obtained above. For electronic or collisional orbital angular momenta, it is common to use \(\textbf{L}^2\) and \(\textbf{L}^z\) ; for electron spin, S2 and Sz are used; for nuclear spin I2 and Iz are most common; and for molecular rotational angular momentum, N2 and Nz are most common (although sometimes \(\textbf{J}^2\) and \(\textbf{J}^z\) may be used). Whenever two or more angular momenta are combined or coupled to produce a total angular momentum, the latter is designated by \(\textbf{J}^2\) and \(\textbf{J}^z\).
2.7.4. Coupling of Angular Momenta
If the Hamiltonian under study contains terms that couple two or more angular momenta J(i), then only the components of the total angular momentum J =\sum_iJ(i) and the total \textbf{J}^2 will commute with H. It is therefore essential to label the quantum states of the system by the eigenvalues of \textbf{J}_z and \textbf{J}^2 and to construct variational trial or model wave functions that are eigenfunctions of these total angular momentum operators. The problem of angular momentum coupling has to do with how to combine eigenfunctions of the uncoupled angular momentum operators, which are given as simple products of the eigenfunctions of the individual angular momenta \Pi_i |j_i,m_i>, to form eigenfunctions of \textbf{J}^2 and \textbf{J}_z.
a. Eigenfunctions of \(\textbf{J}_z\)
Because the individual elements of J are formed additively, but \(\textbf{J}^2\) is not, it is straightforward to form eigenstates of
\[\textbf{J}_z =\sum_i\textbf{J}_z(i);\]
simple products of the form \(\Pi_i |j_i,m_i>\) are eigenfunctions of \(\textbf{J}_z\):
\[\textbf{J}_z \Pi_i |j_i,m_i> = \sum_k \textbf{J}_z(k) \Pi_i |j_i,m_i> = \sum_k \hbar m_k \Pi_i |j_i,m_i>,\]
and have \(\textbf{J}_z\) eigenvalues equal to the sum of the individual \(m_k\hbar\) eigenvalues. Hence, to form an eigenfunction with specified J and M eigenvalues, one must combine only those product states \(\Pi_i |j_i,m_i>\) whose \(m_i\hbar\) sum is equal to the specified M value.
b. Eigenfunctions of \(\textbf{J}^2\); the Clebsch-Gordon Series
The task is then reduced to forming eigenfunctions \(|J,M>\), given particular values for the {ji} quantum numbers. When coupling pairs of angular momenta { \(|j,m>\) and |j',m'>}, the total angular momentum states can be written, according to what we determined above, as
\[|J,M> = \sum_{m,m'} CJ,Mj,m;j',m' |j,m> |j',m'>,\]
where the coefficients CJ,Mj,m;j',m' are called vector coupling coefficients (because angular momentum coupling is viewed much like adding two vectors j and j' to produce another vector J), and where the sum over m and m' is restricted to those terms for which m+m' = M. It is more common to express the vector coupling or so-called Clebsch-Gordon (CG) coefficients as <j,m;j'm'|J,M> and to view them as elements of a matrix whose columns are labeled by the coupled-state J,M quantum numbers and whose rows are labeled by the quantum numbers characterizing the uncoupled product basis j,m;j',m'. It turns out that this matrix can be shown to be unitary so that the CG coefficients obey:
\[\sum_{m,m'} <j,m;j'm'|J,M>* <j,m;j'm'|J',M'> = \delta_{j,j^\prime} \delta_{m,m^\prime}\]
and
\[\sum{J,M} <j,n;j'n'|J,M> <j,m;j'm'|J,M>* = \delta_{n,m} \delta_{n',m'}.\]
This unitarity of the CG coefficient matrix allows the inverse of the relation giving coupled functions in terms of the product functions:
\[|J,M> = \sum_{m,m'} <j,m;j'm'|J,M> |j,m> |j',m'>\]
to be written as:
\[|j,m> |j',m'> = \sum{J,M} <j,m;j'm'|J,M>* |J,M>\]
\[= \sum{J,M} <J,M|j,m;j'm'> |J,M>.\]
This result expresses the product functions in terms of the coupled angular momentum functions.
c. Generation of the CG Coefficients
The CG coefficients can be generated in a systematic manner; however, they can also be looked up in books where they have been tabulated (e.g., see Table 2.4 of R. N. Zare, Angular Momentum, John Wiley, New York (1988)). Here, we will demonstrate the technique by which the CG coefficients can be obtained, but we will do so for rather limited cases and refer the reader to more extensive tabulations for more cases.
The strategy we take is to generate the |J,J> state (i.e., the state with maximum M-value) and to then use \textbf{J}_{-} to generate |J,j-1>, after which the state |j-1,j-1> (i.e., the state with one lower \textbf{J}_{-}value) is constructed by finding a combination of the product states in terms of which |J,j-1> is expressed (because both |J,j-1> and |j-1,j-1> have the same M-value M=j-1) which is orthogonal to |J,j-1> (because |j-1,j-1> and |J,j-1> are eigenfunctions of the Hermitian operator \textbf{J}^2 corresponding to different eigenvalues, they must be orthogonal). This same process is then used to generate |J,\textbf{J}_{-}2> |j-1,\textbf{J}_{-}2> and (by orthogonality construction) |\textbf{J}_{-}2,\textbf{J}_{-}2>, and so on.
i. The States With Maximum and Minimum M-Values
We begin with the state |J,J> having the highest M-value. This state must be formed by taking the highest m and the highest m' values (i.e., m=j and m'=j'), and is given by:
\[|J,J> = |j,j> |j'j'>.\]
Only this one product is needed because only the one term with m=j and m'=j' contributes to the sum in the above CG series. The state
\[|J,-J> = |j,-j> |j',-j'>\]
with the minimum M-value is also given as a single product state.
Notice that these states have M-values given as ±(\textbf{J}_{+}j'); since this is the maximum M-value, it must be that the \textbf{J}_{-}value corresponding to this state is J= \textbf{J}_{+}j'.
ii. States With One Lower M-Value But the Same \textbf{J}_{-}Value
Applying \textbf{J}_{-} to |J,J> , and expressing \textbf{J}_{-} as the sum of lowering operators for the two individual angular momenta:
\[\textbf{J}_{-} = \textbf{J}_{-}(1) + \textbf{J}_{-}(2)\]
gives
\[\textbf{J}_{-}|J,J> = h{J(j+1) -J(j-1)}1/2 |J,j-1>\]
\[= (\textbf{J}_{-}(1) + \textbf{J}_{-}(2)) |j,j> |j'j'>\]
\[= \hbar\sqrt{j(j+1) - j(j-1)} |j,j-1> |j',j'> + \hbar\sqrt{j'(j'+1)-j'(j'-1)} |j,j> |j',j'-1>.\]
This result expresses \(|J,j-1>\) as follows:
\[|J,j-1>= \frac{\sqrt{j(j+1)-j(j-1)} |j,j-1> |j',j'>+ \sqrt{j'(j'+1)-j'(j'-1)} |j,j> |j',j'-1>}{\sqrt{J(j+1) -J(j-1)}};\]
that is, the \(|J,j-1>\) state, which has \(M=j-1\), is formed from the two product states \(|j,j-1> |j',j'>\) and \(|j,j> |j',j'-1>\) that have this same M-value.
iii. States With One Lower \(\textbf{J}_{-}\) Value
To find the state \(|j-1,j-1>\) that has the same M-value as the one found above but one lower \(\textbf{J}_{-}\) value, we must construct another combination of the two product states with \(M=j-1\) (i.e., \(|j,j-1> |j',j'>\) and \(|j,j> |j',j'-1>\)) that is orthogonal to the combination representing \(|J,j-1>\); after doing so, we must scale the resulting function so it is properly normalized. In this case, the desired function is:
\[|j-1,j-1>= [{j(j+1)-j(j-1)}1/2 |j,j> |j',j'-1>\]
\[- {j'(j'+1)-j'(j'-1)}1/2 |j,j-1> |j',j'>] {J(j+1) -J(j-1)}-1/2 .\]
It is straightforward to show that this function is indeed orthogonal to \(|J,j-1>\).
iv. States With Even One Lower \(\textbf{J}_{-}\) Value
Having expressed |J,j-1> and |j-1,j-1> in terms of |j,j-1> |j',j'> and |j,j> |j',j'-1>, we are now prepared to carry on with this stepwise process to generate the states |J,\textbf{J}_{-}2>, |j-1,\textbf{J}_{-}2> and |\textbf{J}_{-}2,\textbf{J}_{-}2> as combinations of the product states with M=\textbf{J}_{-}2. These product states are |j,j-2> |j',j'>, |j,j> |j',j'-2>, and |j,j-1> |j',j'-1>. Notice that there are precisely as many product states whose m+m' values add up to the desired M-value as there are total angular momentum states that must be constructed (there are three of each in this case).
The steps needed to find the state |\textbf{J}_{-}2,\textbf{J}_{-}2> are analogous to those taken above:
a. One first applies \textbf{J}_{-} to |j-1,j-1> and to |J,j-1> to obtain |j-1,\textbf{J}_{-}2> and |J,\textbf{J}_{-}2>, respectively as combinations of |j,j-2> |j',j'>, |j,j> |j',j'-2>, and |j,j-1> |j',j'-1>.
b. One then constructs |\textbf{J}_{-}2,\textbf{J}_{-}2> as a linear combination of the |j,j-2> |j',j'>, |j,j> |j',j'-2>, and |j,j-1> |j',j'-1> that is orthogonal to the combinations found for |j-1,\textbf{J}_{-}2> and |J,\textbf{J}_{-}2>.
Once |\textbf{J}_{-}2,\textbf{J}_{-}2> is obtained, it is then possible to move on to form |J,\textbf{J}_{-}3>, |j-1,\textbf{J}_{-}3>, and |\textbf{J}_{-}2,\textbf{J}_{-}3> by applying \textbf{J}_{-} to the three states obtained in the preceding application of the process, and to then form |\textbf{J}_{-}3,\textbf{J}_{-}3> as the combination of |j,j-3> |j',j'>, |j,j> |j',j'-3>,
|j,j-2> |j',j'-1>, |j,j-1> |j',j'-2> that is orthogonal to the combinations obtained for |J,\textbf{J}_{-}3>, |j-1,\textbf{J}_{-}3>, and |\textbf{J}_{-}2,\textbf{J}_{-}3>.
Again notice that there are precisely the correct number of product states (four here) as there are total angular momentum states to be formed. In fact, the product states and the total angular momentum states are equal in number and are both members of orthonormal function sets (because \textbf{J}^2(1), \textbf{J}_z(1), \textbf{J}^2(2), and \textbf{J}_z(2) as well as \textbf{J}^2 and \textbf{J}_z are Hermitian operators which have complete sets of orthonormal eigenfunctions). This is why the CG coefficient matrix is unitary; because it maps one set of orthonormal functions to another, with both sets containing the same number of functions.
d. An Example
Let us consider an example in which the spin and orbital angular momenta of the \sum_i atom in its 3P ground state can be coupled to produce various 3PJ states. In this case, the specific values for j and j' are j=S=1 and j'=L=1. We could, of course take j=L=1 and j'=S=1, but the final wave functions obtained would span the same space as those we are about to determine.
The state with highest M-value is the 3P(Ms=1, M_L=1) state, which can be represented by the product of an \alpha\alpha spin function (representing S=1, Ms=1) and a 3p_13p_0 spatial function (representing L=1, M_L=1), where the first function corresponds to the first open-shell orbital and the second function to the second open-shell orbital. Thus, the maximum M-value is M= 2 and corresponds to a state with J=2:
\[J=2,M=2> = |2,2> = \alpha\alpha 3p_13p_0 .\]
Clearly, the state |2,-2> would be given as \(\beta\beta 3p_{-1}3p_0\).
The states |2,1> and |1,1> with one lower M-value are obtained by applying \(\textbf{J}_{-} = \textbf{S}_{-} + \textbf{L}_{-}\) to \(|2,2>\) as follows:
\[\textbf{J}_{-} |2,2> = \hbar\sqrt{J(J+1)-M(M-1)} |2,1> = \hbar\sqrt{2(3)-2(1)} |2,1>\]
\[= (\textbf{S}_{-} + \textbf{L}_{-}) \alpha\alpha 3p_13p_0 .\]
To apply \(\textbf{S}_{-}\) or \(\textbf{L}_{-}\) to \(\alpha\alpha 3p_13p_0\), one must realize that each of these operators is, in turn, a sum of lowering operators for each of the two open-shell electrons:
\[\textbf{S}_{-} = \textbf{S}_{-}(1) + \textbf{S}_{-}(2),\]
\[\textbf{L}_{-} = \textbf{L}_{-}(1) + \textbf{L}_{-}(2).\]
The result above can therefore be continued as
\[(\textbf{S}_{-} + \textbf{L}_{-}) \alpha\alpha 3p_13p_0 = \hbar\sqrt{1/2(3/2)-1/2(-1/2)} \beta\alpha 3p_13p_0\]
\[+ \hbar\sqrt{1/2(3/2)-1/2(-1/2)} \alpha\beta 3p_13p_0\]
\[+ \hbar\sqrt{1(2)-1(0)} \alpha\alpha 3p_03p_0\]
\[+ \hbar\sqrt{1(2)-0(-1)} \alpha\alpha 3p_13p_{-1}.\]
So, the function \(|2,1>\) is given by
\[|2,1> = [\beta\alpha 3p_13p_0 + ab 3p_13p_0 + \sqrt{2} \alpha\alpha 3p_03p_0+ \sqrt{2} \alpha\alpha 3p_13p_{-1}]/2,\]
which can be rewritten as:
\[|2,1> = [(\beta\alpha + ab)^3p_13p_0 + \sqrt{2} \alpha\alpha (3p_03p_0 + 3p_13p_{-1})]/2.\]
Writing the result in this way makes it clear that |2,1> is a combination of the product states \(|S=1,M_S=0> |L=1,M_L=1>\) (the terms containing \(|S=1,M_S=0> = \frac{1}{\sqrt{2}}(\alpha\beta+\beta\alpha))\) and \(|S=1,M_S=1> |L=1,M_L=0>\) (the terms containing |S=1,M_S=1> = \alpha\alpha).
There is a good chance that some readers have noticed that some of the terms in the \(|2,1>\) function would violate the Pauli exclusion principle. In particular, the term \(\alpha\alpha 3p_03p_0\) places two electrons into the same orbitals and with the same spin. Indeed, this electronic function would indeed violate the Pauli principle, and it should not be allowed to contribute to the final Si 3PJ wave functions we are trying to form. The full resolution of how to deal with this paradox is given in the following Subsection, but for now let me say the following:
(i) Once you have learned that all of the spin-orbital product functions shown for |2,1> (e.g., \(\alpha\alpha 3p_03p_0\) , \((\beta\alpha + \alpha\beta)^3p_13p_0 \), and \(\alpha\alpha 3p_13p_{-1}\)) represent Slater determinants (we deal with this in the next Subsection) that are antisymmetric with respect to permutation of any pair of electrons, you will understand that the Slater determinant corresponding to \(\alpha\alpha 3p_03p_0\) vanishes.
(ii) If, instead of considering the \(3s^2 3p^2\) configuration of Si, we wanted to generate wave functions for the \(3s^2 3p^1 4p^1\) 3PJ states of Si, the same analysis as shown above would pertain, except that now the \(|2,1>\) state would have a contribution from \(\alpha\alpha 3p_04p_0\). This contribution does not violate the Pauli principle, and its Slater determinant does not vanish.
So, for the remainder of this treatment of the 3PJ states of Si, don’t worry about terms arising that violate the Pauli principle; they will not contribute because their Slater determinants will vanish.
To form the other function with M=1, the |1,1> state, we must find another combination of |S=1,M_S=0> |L=1,M_L=1> and |S=1,M_S=1> |L=1,M_L=0> that is orthogonal to |2,1> and is normalized. Since
\[|2,1> = \frac{1}{\sqrt{2}} [|S=1,M_S=0> |L=1,M_L=1> + |S=1,M_S=1> |L=1,M_L=0>],\]
we immediately see that the requisite function is
\[|1,1> = \frac{1}{\sqrt{2}} [|S=1,M_S=0> |L=1,M_L=1> - |S=1,M_S=1> |L=1,M_L=0>].\]
In the spin-orbital notation used above, this state is:
\[|1,1> = [(\beta\alpha + ab)^3p_13p_0 - \sqrt{2} \alpha\alpha (3p_03p_0 + 3p_13p_{-1})]/2.\]
Thus far, we have found the 3PJ states with J=2, M=2; J=2, M=1; and J=1, M=1.
To find the 3PJ states with J=2, M=0; J=1, M=0; and J=0, M=0, we must once again apply the \textbf{J}_{-} tool. In particular, we apply \textbf{J}_{-} to |2,1> to obtain |2,0> and we apply \textbf{J}_{-} to |1,1> to obtain |1,0>, each of which will be expressed in terms of |S=1,M_S=0> |L=1,M_L=0>, |S=1,M_S=1> |L=1,M_L=-1>, and |S=1,M_S=-1> |L=1,M_L=1>. The |0,0> state is then constructed to be a combination of these same product states which is orthogonal to |2,0> and to |1,0>. The results are as follows:
\[|J=2,M=0> = \frac{1}{\sqrt{6}}[2 |1,0> |1,0> + |1,1> |1,-1> + |1,-1> |1,1>],\]
\[|J=1,M=0> = \frac{1}{\sqrt{2}}[|1,1> |1,-1> - |1,-1> |1,1>],\]
\[|J=0, M=0> = \frac{1}{\sqrt{3}}[|1,0> |1,0> - |1,1> |1,-1> - |1,-1> |1,1>],\]
where, in all cases, a short hand notation has been used in which the \(|S,M_S> |L,M_L>\) product stated have been represented by their quantum numbers with the spin function always appearing first in the product. To finally express all three of these new functions in terms of spin-orbital products it is necessary to give the \(|S,M_S> |L,M_L>\) products with M=0 in terms of these products. For the spin functions, we have:
\[|S=1,M_S=1> = \alpha\alpha,\]
\[|S=1,M_S=0> = \frac{1}{\sqrt{2}}(\alpha\beta+\beta\alpha).\]
\[|S=1,M_S=-1> = \beta\beta.\]
For the orbital product function, we have:
\[|L=1, M_L=1> = 3p_13p_0 ,\\]
\[|L=1,M_L=0> = \frac{1}{\sqrt{2}}(3p_03p_0 + 3p_13p_{-1}),\]
\[|L=1, M_L=-1> = 3p_03p_{-1}.\]
e. Coupling Angular Momenta of Equivalent Electrons
If equivalent angular momenta are coupled (e.g., to couple the orbital angular momenta of a p2 or d3 configuration), there is a tool one can use to determine which of the term symbols violate the Pauli principle. To carry out this step, one forms all possible unique (determinental) product states with non-negative ML and MS values and arranges them into groups according to their ML and MS values. For example, the “boxes” appropriate to the p2 orbital occupancy that we considered earlier for \sum_i are shown below:
ML 2 1 0
---------------------------------------------------------
MS 1 |p_1ap_0a| |p_1ap_{-1}a|
0 |p_1ap_1b| |p_1ap_0b|, |p_0ap_1b| |p_1ap_{-1}b|,
|p_{-1}ap_1b|,
|p_0ap_0b|
There is no need to form the corresponding states with negative ML or negative MS values because they are simply "mirror images" of those listed above. For example, the state with M_L= -1 and MS = -1 is |p_{-1}bp_0b|, which can be obtained from the ML = 1, MS = 1 state |p_1ap_0a| by replacing a by b and replacing p_1 by p_{-1}.
Given the box entries, one can identify those term symbols that arise by applying the following procedure over and over until all entries have been accounted for:
i. One identifies the highest MS value (this gives a value of the total spin quantum number that arises, S) in the box. For the above example, the answer is S = 1.
ii. For all product states of this MS value, one identifies the highest ML value (this gives a value of the total orbital angular momentum, L, that can arise for this S). For the above example, the highest ML within the MS =1 states is ML = 1 (not ML = 2), hence L=1.
iii. Knowing an S, L combination, one knows the first term symbol that arises from this configuration. In the p2 example, this is 3P.
iv. Because the level with this L and S quantum numbers contains (2L+1)(2S+1) states with ML and MS quantum numbers running from -L to L and from -S to S, respectively, one must remove from the original box this number of product states. To do so, one simply erases from the box one entry with each such ML and MS value. Actually, since the box need only show those entries with non-negative ML and MS values, only these entries need be explicitly deleted. In the 3P example, this amounts to deleting nine product states with ML, MS values of 1,1; 1,0; 1,-1; 0,1; 0,0; 0,-1; -1,1; -1,0; -1,-1.
v. After deleting these entries, one returns to step 1 and carries out the process again. For the p2 example, the box after deleting the first nine product states looks as follows (those that appear in italics should be viewed as already deleted in counting all of the 3P states):
ML 2 1 0
---------------------------------------------------------
MS 1 |p_1ap_0a| |p_1ap_{-1}a|
0 |p_1ap_1b| |p_1ap_0b|, |p_0ap_1b| |p_1ap_{-1}b|,
|p_{-1}ap_1b|,
|p_0ap_0b|
It should be emphasized that the process of deleting or crossing off entries in various ML, MS boxes involves only counting how many states there are; by no means do we identify the particular L,S,ML,MS wave functions when we cross out any particular entry in a box. For example, when the |p_1ap_0b| product is deleted from the M_L= 1, M_S=0 box in accounting for the states in the 3P level, we do not claim that |p_1ap_0b| itself is a member of the 3P level; the |p_0ap_1b| product state could just as well been eliminated when accounting for the 3P states.
Returning to the p2 example at hand, after the 3P term symbol's states have been accounted for, the highest MS value is 0 (hence there is an S=0 state), and within this MS value, the highest ML value is 2 (hence there is an L=2 state). This means there is a 1D level with five states having ML = 2,1,0,-1,-2. Deleting five appropriate entries from the above box (again denoting deletions by italics) leaves the following box:
ML 2 1 0
---------------------------------------------------------
MS 1 |p_1ap_0a| |p_1ap_{-1}a|
0 |p_1ap_1b| |p_1ap_0b|, |p_0ap_1b| |p_1ap_{-1}b|,
|p_{-1}ap_1b|,
|p_0ap_0b|
The only remaining entry, which thus has the highest MS and ML values, has MS = 0 and ML = 0. Thus there is also a 1S level in the p2 configuration.
Thus, unlike the non-equivalent 3p_14p_1 case, in which 3P, 1P, 3D, 1D, 3S, and 1S levels arise, only the 3P, 1D, and 1S arise in the p2 situation. This "box method" is useful to carry out whenever one is dealing with equivalent angular momenta.
If one has mixed equivalent and non-equivalent angular momenta, one can determine all possible couplings of the equivalent angular momenta using this method and then use the simpler vector coupling method to add the non-equivalent angular momenta to each of these coupled angular momenta. For example, the p2d1 configuration can be handled by vector coupling (using the straightforward non-equivalent procedure) L=2 (the d orbital) and S=1/2 (the third electron's spin) to each of 3P, 1D, and 1S arising from the p2 configuration. The result is 4F, 4D, 4P, 2F, 2D, 2P, 2G, 2F, 2D, 2P, 2S, and 2D.
2.8. Rotations of Molecules
2.8.1. Rotational Motion For Rigid Diatomic and Linear Polyatomic Molecules
This Schrödinger equation relates to the rotation of diatomic and linear polyatomic molecules. It also arises when treating the angular motions of electrons in any spherically symmetric potential.
A diatomic molecule with fixed bond length R rotating in the absence of any external potential is described by the following Schrödinger equation:
\[- \frac{\hbar^2}{2\mu} \left{\frac{1}{R^2\sin\theta}\frac{\partial}{\partial \theta} (\sin\theta \frac{\partial}{\partial \theta} + \frac{R^2\sin^2\theta} \frac{\partial^2}{\partial \phi^2\right} \psi = E \psi\]
or
\[\frac{\textbf{L}^2\psi}{2\mu R^2} = E \psi,\]
where \(\textbf{L}^2\) is the square of the total angular momentum operator \(\textbf{L}_x^2 + \textbf{L}_y^2 + \textbf{L}_z^2\) expressed in polar coordinates above. The angles q and f describe the orientation of the diatomic molecule's axis relative to a laboratory-fixed coordinate system, and m is the reduced mass of the diatomic molecule \(\mu=m_1m_2/(m_1+m_2)\). The differential operators can be seen to be exactly the same as those that arose in the hydrogen-like-atom case discussed earlier in this Chapter. Therefore, the same spherical harmonics that served as the angular parts of the wave function in the hydrogen-atom case now serve as the entire wave function for the so-called rigid rotor: \(\psi = Y_{J,M}(\theta,\phi)\). These are exactly the same functions as we plotted earlier when we graphed the s (L=0), p (L=1), and d (L=2) orbitals. The energy eigenvalues corresponding to each such eigenfunction are given as:
\[E_J = \frac{\hbar^2 J(J+1)}{2\mu R^2} = B J(J+1)\]
and are independent of M. Thus each energy level is labeled by J and is 2J+1-fold degenerate (because M ranges from -J to J). Again, this is just like we saw when we looked at the hydrogen orbitals; the p orbitals are 3-fold degenerate and the d orbitals are 5-fold degenerate. The so-called rotational constant B (defined as \(\hbar^2/2\mu R^2\)) depends on the molecule's bond length and reduced mass. Spacings between successive rotational levels (which are of spectroscopic relevance because, as shown in Chapter 6, angular momentum selection rules often restrict the changes DJ in J that can occur upon photon absorption to 1,0, and -1) are given by
\[\Delta E = B (J+1)(J+2) - B J(J+1) = 2B(J+1).\]
These energy spacings are of relevance to microwave spectroscopy which probes the rotational energy levels of molecules. In fact, microwave spectroscopy offers the most direct way to determine molecular rotational constants and hence molecular bond lengths.
The rigid rotor provides the most commonly employed approximation to the rotational energies and wave functions of linear molecules. As presented above, the model restricts the bond length to be fixed. Vibrational motion of the molecule gives rise to changes in \(R\), which are then reflected in changes in the rotational energy levels (i.e., there are different \(B\) values for different vibrational levels). The coupling between rotational and vibrational motion gives rise to rotational \(B\) constants that depend on vibrational state as well as dynamical couplings, called centrifugal distortions, which cause the total ro-vibrational energy of the molecule to depend on rotational and vibrational quantum numbers in a non-separable manner.
Within this rigid rotor model, the absorption spectrum of a rigid diatomic molecule should display a series of peaks, each of which corresponds to a specific \(J \rightarrow J + 1\) transition. The energies at which these peaks occur should grow linearly with \(J\) as shown above. An example of such a progression of rotational lines is shown in the Fig. 2.23.
Figure 2.23. Typical rotational absorption profile showing intensity vs. J value of the absorbing level
The energies at which the rotational transitions occur appear to fit the \(\Delta E = 2B (J+1)\) formula rather well. The intensities of transitions from level J to level J+1 vary strongly with J primarily because the population of molecules in the absorbing level varies with J. These populations PJ are given, when the system is at equilibrium at temperature T, in terms of the degeneracy (2J+1) of the Jth level and the energy of this level B J(J+1) by the Boltzmann formula:
\[P_J = \frac{1}{Q} (2J+1) \exp(-BJ(J+1)/kT),\]
where Q is the rotational partition function:
\[Q = \sum_J (2J+1) \exp(-BJ(J+1)/kT).\]
For low values of J, the degeneracy is low and the \(\exp(-BJ(J+1)/kT)\) factor is near unity. As \(J\) increases, the degeneracy grows linearly but the \(\exp(-BJ(J+1)/kT)\) factor decreases more rapidly. As a result, there is a value of \(J\), given by taking the derivative of \((2J+1) \exp(-BJ(J+1)/kT)\) with respect to \(J\) and setting it equal to zero,
\[2J_{\rm max}+ 1 =\sqrt{\frac{2kT}{B}}\]
at which the intensity of the rotational transition is expected to reach its maximum. This behavior is clearly displayed in the above figure.
The eigenfunctions belonging to these energy levels are the spherical harmonics YL,M(\theta,\phi) which are normalized according to
\[\int_0^\pi\int_0^{2\pi}Y_{L,M}^*(\theta,\phi)Y_{L',M'}(\theta,\phi)sin\theta d\theta d\phi= \delta_{L,L'} \delta_{m,m^\prime} .\]
As noted above, these functions are identical to those that appear in the solution of the angular part of Hydrogenic atoms. The above energy levels and eigenfunctions also apply to the rotation of rigid linear polyatomic molecules; the only difference is that the moment of inertia I entering into the rotational energy expression, which is \(\mu R^2\) for a diatomic, is given by
\[I = \sum_a m_a R_a^2\]
where ma is the mass of the ath atom and \(R_a\) is its distance from the center of mass of the molecule to this atom.
2.8.2. Rotational Motions of Rigid Non-Linear Molecules
a. The Rotational Kinetic Energy
The classical rotational kinetic energy for a rigid polyatomic molecule is
\[H_{\rm rot} = \frac{J_a^2}{2I_a} + \frac{J_b^2}{2I_b} + \frac{J_c^2}{2I_c}\]
where the \(I_k (k = a, b, c)\) are the three principal moments of inertia of the molecule (the eigenvalues of the moment of inertia tensor). This tensor has elements in a Cartesian coordinate system (\(K, K' = X, Y, Z\)), whose origin is located at the center of mass of the molecule, that can be computed as:
\[I_{K,K} = \sum_j m_j (R_j^2 - R_{K,j}^2) (\text{for }K = K')\]
\[I_{K,K'} = - \sum_j m_j R_{K,j} R_{K',j} (\text{for } K \ne K').\]
As discussed in more detail in R. N. Zare, Angular Momentum, John Wiley, New York (1988), the components of the corresponding quantum mechanical angular momentum operators along the three principal axes are:
\[\textbf{J}_a = -i\hbar \cos\chi [\cot\theta \frac{\partial}{\partial \chi} - \frac{1}{\sin\theta}\frac{\partial}{\partial \phi} ] -i\hbar \sin\chi \frac{\partial}{\partial \theta}\]
\[\textbf{J}_b = i\hbar \sin\chi [\cot\theta \frac{\partial}{\partial \chi} - \frac{1}{\sin\theta}\frac{\partial}{\partial \phi}] -i\hbar \cos\chi \frac{\partial}{\partial \theta}\]
\[\textbf{J}_c = - i\hbar \frac{\partial}{\partial \chi} .\]
The angles \(\theta\), \(\phi\), and \(\chi\) are the Euler angles needed to specify the orientation of the rigid molecule relative to a laboratory-fixed coordinate system. The corresponding square of the total angular momentum operator \(\textbf{J}^2\) can be obtained as
\[\textbf{J}^2 = \textbf{J}_a^2 + \textbf{J}_b^2 + \textbf{J}_c^2\]
\[= - \hbar^2 \frac{\partial^2}{\partial \theta^2} - \hbar^2\cot\theta \frac{\partial}{\partial \theta} + \hbar^2 \frac{1}{\sin^2\theta} \left(\frac{\partial^2}{\partial \phi^2} + \frac{\partial^2}{\partial \chi^2} - 2 \cos\theta\frac{\partial^2}{\partial \phi\partial \chi} \right),\]
and the component along the la\beta - fixed Z axis \(J_Z\) is \(- i\hbar \partial /\partial \phi\) as we saw much earlier in this text.
b. The Eigenfunctions and Eigenvalues for Special Cases
i. Spherical Tops
When the three principal moment of inertia values are identical, the molecule is termed a spherical top. In this case, the total rotational energy can be expressed in terms of the total angular momentum operator \(\textbf{J}^2 \)
\[H_{\rm rot} = \frac{\textbf{J}^2}{2I}.\]
As a result, the eigenfunctions of \(H_{\rm rot}\) are those of \(\textbf{J}^2\) and \(J_a\) as well as \(J_Z\) both of which commute wit\hbar \textbf{J}^2 and with one another. \(J_Z\) is the component of J along the la\beta - fixed Z-axis and commutes with \(J_a\) because \(J_Z = - i\hbar \partial /\partial \phi\) and \(J_a = - i\hbar \partial /\partial \chi\) act on different angles. The energies associated with such eigenfunctions are
\[E(J,K,M) = \frac{\hbar^2 J(J+1)}{2I^2},\]
for all K (i.e., \(J_a\) quantum numbers) ranging from -J to J in unit steps and for all M (i.e., \(J_Z\) quantum numbers) ranging from -J to J. Each energy level is therefore \((2J + 1)^2\) degenerate because there are 2J + 1 possible K values and \(2J + 1\) possible \(M\) values for each \(J\).
The eigenfunctions \(|J,M,K>\) of \(\textbf{J}^2\), \(J_Z\) and \(J_a\) , are given in terms of the set of so-called rotation matrices \(D_{J,M,K}\):
\[|J,M,K> = \sqrt{\frac{2J+1}{8\pi^2}}D^*_{J,M,K}(\theta,\phi,\chi)\]
which obey
\[\textbf{J}^2|J,M,K> = \hbar^2 J(J+1) |J,M,K>,\]
\[\textbf{J}_a |J,M,K> = \hbar K |J,M,K>,\]
\[\textbf{J}_Z |J,M,K> = \hbar M |J,M,K>.\]
These \(D_{J,M,K}\) functions are proportional to the spherical harmonics \(Y_{J,M}(\theta,\phi)\) multiplied by \(\exp(iK\chi)\), which reflects its c-dependence.
ii. Symmetric Tops
Molecules for which two of the three principal moments of inertia are equal are called symmetric tops. Those for which the unique moment of inertia is smaller than the other two are termed prolate symmetric tops; if the unique moment of inertia is larger than the others, the molecule is an oblate symmetric top. An American football is prolate, and a Frisbee is oblate.
Again, the rotational kinetic energy, which is the full rotational Hamiltonian, can be written in terms of the total rotational angular momentum operator \textbf{J}^2 and the component of angular momentum along the axis with the unique principal moment of inertia:
\[\textbf{H}_{\rm rot} = \frac{\textbf{J}^2}{2I} + \textbf{J}_a^2\left[\frac{1}{2I_a} - \frac{1}{2I}\right]\text{, for prolate tops}\]
\[\textbf{H}_{\rm rot} = \frac{\textbf{J}^2}{2I} + \textbf{J}_c^2\left[\frac{1}{2I_c} - \frac{1}{2I}\right]\text{, for oblate tops}\]
Here, the moment of inertia I denotes that moment that is common to two directions; that is, I is the non-unique moment of inertia. As a result, the eigenfunctions of \(H_{\rm rot}\) are those of \(\textbf{J}^2\) and \(J_a\) or \(J_c\) (and of \(J_Z\)), and the corresponding energy levels are:
\[E(J,K,M) = \frac{\hbar^2 J(J+1)}{2I^2} + \hbar^2 K^2 \left[\frac{1}{2I_a} - \frac{1}{2I}\right],\]
for prolate tops
\[E(J,K,M) = \frac{\hbar^2 J(J+1)}{2I^2} + \hbar^2 K^2 \left[\frac{1}{2I_c} - \frac{1}{2I}\right],\]
for oblate tops, again for K and M (i.e., \(J_a\) or \(J_c\) and \(J_Z\) quantum numbers, respectively) ranging from -J to J in unit steps. Since the energy now depends on K, these levels are only 2J + 1 degenerate due to the 2J + 1 different M values that arise for each J value. Notice that for prolate tops, because Ia is smaller than I, the energies increase with increasing K for given J. In contrast, for oblate tops, since Ic is larger than I, the energies decrease with K for given J. The eigenfunctions |J, M,K> are the same rotation matrix functions as arise for the spherical-top case, so they do not require any further discussion at this time.
iii. Asymmetric Tops
The rotational eigenfunctions and energy levels of a molecule for which all three principal moments of inertia are distinct (a so-called asymmetric top) cannot analytically be expressed in terms of the angular momentum eigenstates and the J, M, and K quantum numbers. In fact, no one has ever solved the corresponding Schrödinger equation for this case. However, given the three principal moments of inertia Ia, Ib, and Ic, a matrix representation of each of the three contributions to the rotational Hamiltonian
\[H_{\rm rot} = \frac{\textbf{J}_a^2}{2I_a} + \frac{\textbf{J}_b^2}{2I_b} + \frac{\textbf{J}_c^2}{2I_c}\]
can be formed within a basis set of the {|J, M, K>} rotation-matrix functions discussed earlier. This matrix will not be diagonal because the |J, M, K> functions are not eigenfunctions of the asymmetric top H_{\rm rot}. However, the matrix can be formed in this basis and subsequently brought to diagonal form by finding its eigenvectors {Cn, J,M,K} and its eigenvalues {En}. The vector coefficients express the asymmetric top eigenstates as
\[\psi_n (\theta,\phi,\chi) = \sum_{J, M, K} C_{n, J,M,K} |J, M, K>.\]
Because the total angular momentum \textbf{J}^2 still commutes with H_{\rm rot}, each such eigenstate will contain only one \textbf{J}_{-}value, and hence yn can also be labeled by a J quantum number:
\[\psi_{n,J} (\theta,\phi,\chi) = \sum_{M, K} C_{n, J,M,K} |J, M, K>.\]
To form the only non-zero matrix elements of \(H_{\rm rot}\) within the |J, M, K> basis, one can use the following properties of the rotation-matrix functions (see, for example, R. N. Zare, Angular Momentum, John Wiley, New York (1988)):
\[<J, M, K| \textbf{J}_a^2| J, M, K> = <J, M, K| \textbf{J}_b^2| J, M, K>\]
\[= 1/2 <J, M, K| \textbf{J}^2 - \textbf{J}_c^2 | J, M, K> = \hbar^2 [ J(J+1) - K^2 ],\]
\[<J, M, K| \textbf{J}_c^2| J, M, K> = \hbar^2 K^2,\]
\[<J, M, K| \textbf{J}_a^2| J, M, K ± 2> = - <J, M, K| \textbf{J}_b^2| J, M, K ± 2>\]
\[= \hbar^2 \sqrt{J(J+1) - K(K± 1)} \sqrt{J(J+1) -(K± 1)(K± 2)}\]
\[<J, M, K| \textbf{J}_c^2| J, M, K ± 2> = 0.\]
Each of the elements of \(\textbf{J}_c^2\), \(\textbf{J}_a^2\), and \(\textbf{J}_b^2\) must, of course, be multiplied, respectively, by \(1/2I_c\), \(1/2I_a\), and \(1/2I_b\) and summed together to form the matrix representation of \(H_{\rm rot}\). The diagonalization of this matrix then provides the asymmetric top energies and wave functions.
2.9. Vibrations of Molecules
This Schrödinger equation forms the basis for our thinking about bond stretching and angle bending vibrations as well as collective vibrations in solids called phonons.
The radial motion of a diatomic molecule in its lowest (J=0) rotational level can be described by the following Schrödinger equation:
\[- \frac{\hbar^2}{2\mu r^2} \frac{\partial}{\partial r} \left(r^2\frac{\partial \psi}{\partial r}\right) +V(r) \psi = E \psi,\]
where \(\mu\) is the reduced mass \(\mu = m_1m_2/(m_1+m_2)\) of the two atoms. If the molecule is rotating, then the above Schrödinger equation has an additional term \(J(J+1) \hbar^2/2\mu r^{-2} \psi\) on its left-hand side. Thus, each rotational state (labeled by the rotational quantum number J) has its own vibrational Schrödinger equation and thus its own set of vibrational energy levels and wave functions. It is common to examine the \(J=0\) vibrational problem and then to use the vibrational levels of this state as approximations to the vibrational levels of states with non-zero J values (treating the vibration-rotation coupling via perturbation theory). Let us thus focus on the \(J=0\) situation.
By substituting \(\psi= \Phi(r)/r\) into this equation, one obtains an equation for \(\Phi(r)\) in which the differential operators appear to be less complicated:
\[- \frac{\hbar^2}{2\mu} \frac{d^2F}{dr^2} + V(r) \Phi = E F.\]
This equation is exactly the same as the equation seen earlier in this text for the radial motion of the electron in the hydrogen-like atoms except that the reduced mass m replaces the electron mass m and the potential \(V(r)\) is not the Coulomb potential.
If the vibrational potential is approximated as a quadratic function of the bond displacement \(x = r-r_e\) expanded about the equilibrium bond length \(r_e\) where \(V\) has its minimum:
\[V = \frac{1}{2} k(r-r_e)^2,\]
the resulting harmonic-oscillator equation can be solved exactly. Because the potential V grows without bound as x approaches \(\infty\) or \(-\infty\), only bound-state solutions exist for this model problem. That is, the motion is confined by the nature of the potential, so no continuum states exist in which the two atoms bound together by the potential are dissociated into two separate atoms.
In solving the radial differential equation for this potential, the large-r behavior is first examined. For large-r, the equation reads:
\[\frac{d^2F}{dx^2} = \frac{1}{2} k x^2 \frac{2\mu}{\hbar^2} \Phi = \frac{k\mu}{\hbar^2} x^2 F,\]
where \(x = r-r_e\) is the bond displacement away from equilibrium. Defining \(\beta^2 =\frac{k\mu}{\hbar^2}\) and \(\xi= \sqrt{\beta} x\) as a new scaled radial coordinate, and realizing that
\[\frac{d^2}{dx^2} = \beta \frac{d^2}{dx^2}\]
allows the large-r Schrödinger equation to be written as:
\[\frac{d^2F}{d\xi^2} = \xi^2 F\]
which has the solution
\[F_{\rm large-r} = \exp(- \xi^2/2).\]
The general solution to the radial equation is then expressed as this large-r solution multiplied by a power series in the \(z\) variable:
\[\Phi = \exp(- \xi^2/2)\sum_{n=0}\xi^n C_n ,\]
where the \(C_n\) are coefficients to be determined. Substituting this expression into the full radial equation generates a set of recursion equations for the \(C_n\) amplitudes. As in the solution of the hydrogen-like radial equation, the series described by these coefficients is divergent unless the energy \(E\) happens to equal specific values. It is this requirement that the wave function not diverge so it can be normalized that yields energy quantization. The energies of the states that arise by imposing this non-divergence condition are given by:
\[E_n = \hbar \sqrt{\frac{k}{\mu}} (n+\frac{1}{2}),\]
and the eigenfunctions are given in terms of the so-called Hermite polynomials Hn(y) as follows:
\[\psi_n(x) = \frac{1}{\sqrt{n! 2^n}} \left(\frac{\beta}{\pi}\right)^{1/4} \exp(- \beta \xi^2/2) H_n(\sqrt{\beta} x),\]
where \(\beta =\sqrt{\frac{k}{\mu}}\). Within this harmonic approximation to the potential, the vibrational energy levels are evenly spaced:
\[\Delta E = E_{n+1} - E_n = \hbar \sqrt{\frac{k}{\mu}} .\]
In experimental data such evenly spaced energy level patterns are seldom seen; most commonly, one finds spacings \(E_{n+1} - E_n\) that decrease as the quantum number \(n\) increases. In such cases, one says that the progression of vibrational levels displays anharmonicity.
Because the Hermite functions \(H_n\) are odd or even functions of x (depending on whether n is odd or even), the wave functions yn(x) are odd or even. This splitting of the solutions into two distinct classes is an example of the effect of symmetry; in this case, the symmetry is caused by the symmetry of the harmonic potential with respect to reflection through the origin along the x-axis (i.e., changing x to –x). Throughout this text, many symmetries arise; in each case, symmetry properties of the potential cause the solutions of the Schrödinger equation to be decomposed into various symmetry groupings. Such symmetry decompositions are of great use because they provide additional quantum numbers (i.e., symmetry labels) by which the wave functions and energies can be labeled.
The basic idea underlying how such symmetries split the solutions of the Schrödinger equation into different classes relates to the fact that a symmetry operator (e.g., the reflection plane in the above example) commutes with the Hamiltonian. That is, the symmetry operator \(\textbf{S}\) obeys
\[\textbf{S} \textbf{H} = \textbf{H} \textbf{S}.\]
So \(\textbf{S}\) leaves \(\textbf{H}\) unchanged as it acts on \(\textbf{H}\) (this allows us to pass \(\textbf{S}\) through \(\textbf{H}\) in the above equation). Any operator that leaves the Hamiltonian (i.e., the energy) unchanged is called a symmetry operator.
If you have never learned about how point group symmetry can be used to help simplify the solution of the Schrödinger equation, this would be a good time to interrupt your reading and go to Chapter 4 and read the material there.
The harmonic oscillator energies and wave functions comprise the simplest reasonable model for vibrational motion. Vibrations of a polyatomic molecule are often characterized in terms of individual bond-stretching and angle-bending motions, each of which is, in turn, approximated harmonically. This results in a total vibrational wave function that is written as a product of functions, one for each of the vibrational coordinates.
Two of the most severe limitations of the harmonic oscillator model, the lack of anharmonicity (i.e., non-uniform energy level spacings) and lack of bond dissociation, result from the quadratic nature of its potential. By introducing model potentials that allow for proper bond dissociation (i.e., that do not increase without bound as \(x \rightarrow \infty\)), the major shortcomings of the harmonic oscillator picture can be overcome. The so-called Morse potential (see Fig. 2.24)
\[V(r) = D_e (1-\exp(-a(r-r_e)))^2,\]
is often used in this regard. In this form, the potential is zero at \(r = r_e\), the equilibrium bond length and is equal to \(D_e\) as \(r \rightarrow\infty\). Sometimes, the potential is written as
\[ V(r) = D_e (1-\exp(-a(r-r_e)))^2 -D_e\]
so it vanishes as r \rightarrow\infty and is equal to \(–D_e\) at \(r = r_e\). The latter form is reflected in Fig. 2.24.
Figure 2.24. Morse potential energy as a function of bond length
In the Morse potential function, \(D_e\) is the bond dissociation energy, \(r_e\) is the equilibrium bond length, and \(a\) is a constant that characterizes the steepness of the potential and thus affects the vibrational frequencies. The advantage of using the Morse potential to improve upon harmonic-oscillator-level predictions is that its energy levels and wave functions are also known exactly. The energies are given in terms of the parameters of the potential as follows:
\[E_n = \hbar \sqrt{\frac{k}{\mu}} { (n+\frac{1}{2}) - (n+\frac{1}{2})^2 \hbar \sqrt{\frac{k}{\mu}}/4D_e },\]
where the force constant is given in terms of the Morse potential’s parameters by \(k=2D_e a^2\). The Morse potential supports both bound states (those lying below the dissociation threshold for which vibration is confined by an outer turning point) and continuum states lying above the dissociation threshold (for which there is no outer turning point and thus the no spatial confinement). Its degree of anharmonicity is governed by the ratio of the harmonic energy \(\hbar \sqrt{\frac{k}{\mu}}\) to the dissociation energy \(D_e\).
The energy spacing between vibrational levels \(n\) and \(n+1\) are given by
\[E_{n+1} – E_n = \hbar \sqrt{\frac{k}{\mu}} { 1 - (n+1) \hbar \sqrt{\frac{k}{\mu}}/2D_e }.\]
These spacings decrease until \(n\) reaches the value nmax at which
\[ { 1 - (n_{\rm max}+1) \hbar \sqrt{\frac{k}{\mu}}/2D_e } = 0,\]
after which the series of bound Morse levels ceases to exist (i.e., the Morse potential has only a finite number of bound states) and the Morse energy level expression shown above should no longer be used. It is also useful to note that, if \(\sqrt{2D_e\mu}/[a \hbar]\) becomes too small (i.e., < 1.0 in the Morse model), the potential may not be deep enough to support any bound levels. It is true that some attractive potentials do not have a large enough \(D_e\) value to have any bound states, and this is important to keep in mind. So, bound states are to be expected when there is a potential well (and thus the possibility of inner- and outer- turning points for the classical motion within this well) but only if this well is deep enough.
The eigenfunctions of the harmonic and Morse potentials display nodal character analogous to what we have seen earlier in the particle-in-boxes model problems. Namely, as the energy of the vibrational state increases, the number of nodes in the vibrational wave function also increases. The state having vibrational quantum number v has v nodes. I hope that by now the student is getting used to seeing the number of nodes increase as the quantum number and hence the energy grows. As the quantum number v grows, not only does the wave function have more nodes, but its probability distribution becomes more and more like the classical spatial probability, as expected. In particular for large-v, the quantum and classical probabilities are similar and are large near the outer turning point where the classical velocity is low. They also have large amplitudes near the inner turning point, but this amplitude is rather narrow because the Morse potential drops off strongly to the right of this turning point; in contrast, to the left of the outer turning point, the potential decreases more slowly, so the large amplitudes persist over longer ranges near this turning point.
Contributors
Jack Simons (Henry Eyring Scientist and Professor of Chemistry, U. Utah) Telluride Schools on Theoretical Chemistry
Integrated by Tomoyuki Hayashi (UC Davis)

