4.3: Solution Concentrations
- Page ID
- 19966
The Learning Objective of this Module is to describe the concentrations of solutions quantitatively.
Many people have a qualitative idea of what is meant by concentration. Anyone who has made instant coffee or lemonade knows that too much powder gives a strongly flavored, highly concentrated drink, whereas too little results in a dilute solution that may be hard to distinguish from water. In chemistry, the concentration of a solution is the quantity of a solute that is contained in a particular quantity of solvent or solution. Knowing the concentration of solutes is important in controlling the stoichiometry of reactants for solution reactions. Chemists use many different methods to define concentrations, some of which are described in this section.
Molarity
The most common unit of concentration is molarity, which is also the most useful for calculations involving the stoichiometry of reactions in solution. The molarity (M) is a common unit of concentration and is defined as the number of moles of solute present in exactly 1 L of solution. It is, equivalently, the number of millimoles of solute present in exactly 1 mL of solution:
\( molarity = \dfrac{moles\: of\: solute}{liters\: of\: solution} = \dfrac{mmoles\: of\: solute} {milliliters\: of\: solution} \tag{8.2.1}\)
The units of molarity are therefore moles per liter of solution (mol/L), abbreviated as \(M\). An aqueous solution that contains 1 mol (342 g) of sucrose in enough water to give a final volume of 1.00 L has a sucrose concentration of 1.00 mol/L or 1.00 M. In chemical notation, square brackets around the name or formula of the solute represent the molar concentration of a solute. Therefore,
\([\rm{sucrose}] = 1.00\: M\)
is read as “the concentration of sucrose is 1.00 molar.” The relationships between volume, molarity, and moles may be expressed as either
\( V_L M_{mol/L} = \cancel{L} \left( \dfrac{mol}{\cancel{L}} \right) = moles \tag{8.2.2}\)
or
\( V_{mL} M_{mmol/mL} = \cancel{mL} \left( \dfrac{mmol} {\cancel{mL}} \right) = mmoles \tag{8.2.3}\)
Example 2 illustrates the use of Equation 8.2.2 and Equation 8.2.3.
| Example 2 |
|---|
| Calculate the number of moles of sodium hydroxide (NaOH) in 2.50 L of 0.100 M NaOH. Given: identity of solute and volume and molarity of solution Asked for: amount of solute in moles Strategy: Use either Equation 8.2.2 or Equation 8.2.3, depending on the units given in the problem. Solution: Because we are given the volume of the solution in liters and are asked for the number of moles of substance, Equation 8.2.2 is more useful: \( moles\: NaOH = V_L M_{mol/L} = (2 .50\: \cancel{L} ) \left( \dfrac{0.100\: mol } {\cancel{L}} \right) = 0 .250\: mol\: NaOH \) |
| Exercise 2 |
|---|
| Calculate the number of millimoles of alanine, a biologically important molecule, in 27.2 mL of 1.53 M alanine. Answer: 41.6 mmol |
Concentrations are often reported on a mass-to-mass (m/m) basis or on a mass-to-volume (m/v) basis, particularly in clinical laboratories and engineering applications. A concentration expressed on an m/m basis is equal to the number of grams of solute per gram of solution; a concentration on an m/v basis is the number of grams of solute per milliliter of solution. Each measurement can be expressed as a percentage by multiplying the ratio by 100; the result is reported as percent m/m or percent m/v. The concentrations of very dilute solutions are often expressed in parts per million (ppm), which is grams of solute per 106 g of solution, or in parts per billion (ppb), which is grams of solute per 109 g of solution. For aqueous solutions at 20°C, 1 ppm corresponds to 1 μg per milliliter, and 1 ppb corresponds to 1 ng per milliliter. These concentrations and their units are summarized in Table 8.1.
Table 8.1 Common Units of Concentration
| Concentration | Units |
|---|---|
| m/m | g of solute/g of solution |
| m/v | g of solute/mL of solution |
| ppm | g of solute/106 g of solution |
| μg/mL | |
| ppb | g of solute/109 g of solution |
| ng/mL |
The Preparation of Solutions
To prepare a solution that contains a specified concentration of a substance, it is necessary to dissolve the desired number of moles of solute in enough solvent to give the desired final volume of solution. Figure 8.2.1 illustrates this procedure for a solution of cobalt(II) chloride dihydrate in ethanol. Note that the volume of the solvent is not specified. Because the solute occupies space in the solution, the volume of the solvent needed is almost always less than the desired volume of solution. For example, if the desired volume were 1.00 L, it would be incorrect to add 1.00 L of water to 342 g of sucrose because that would produce more than 1.00 L of solution. As shown in Figure 8.2.2, for some substances this effect can be significant, especially for concentrated solutions.

Figure 8.2.1 Preparation of a Solution of Known Concentration Using a Solid Solute
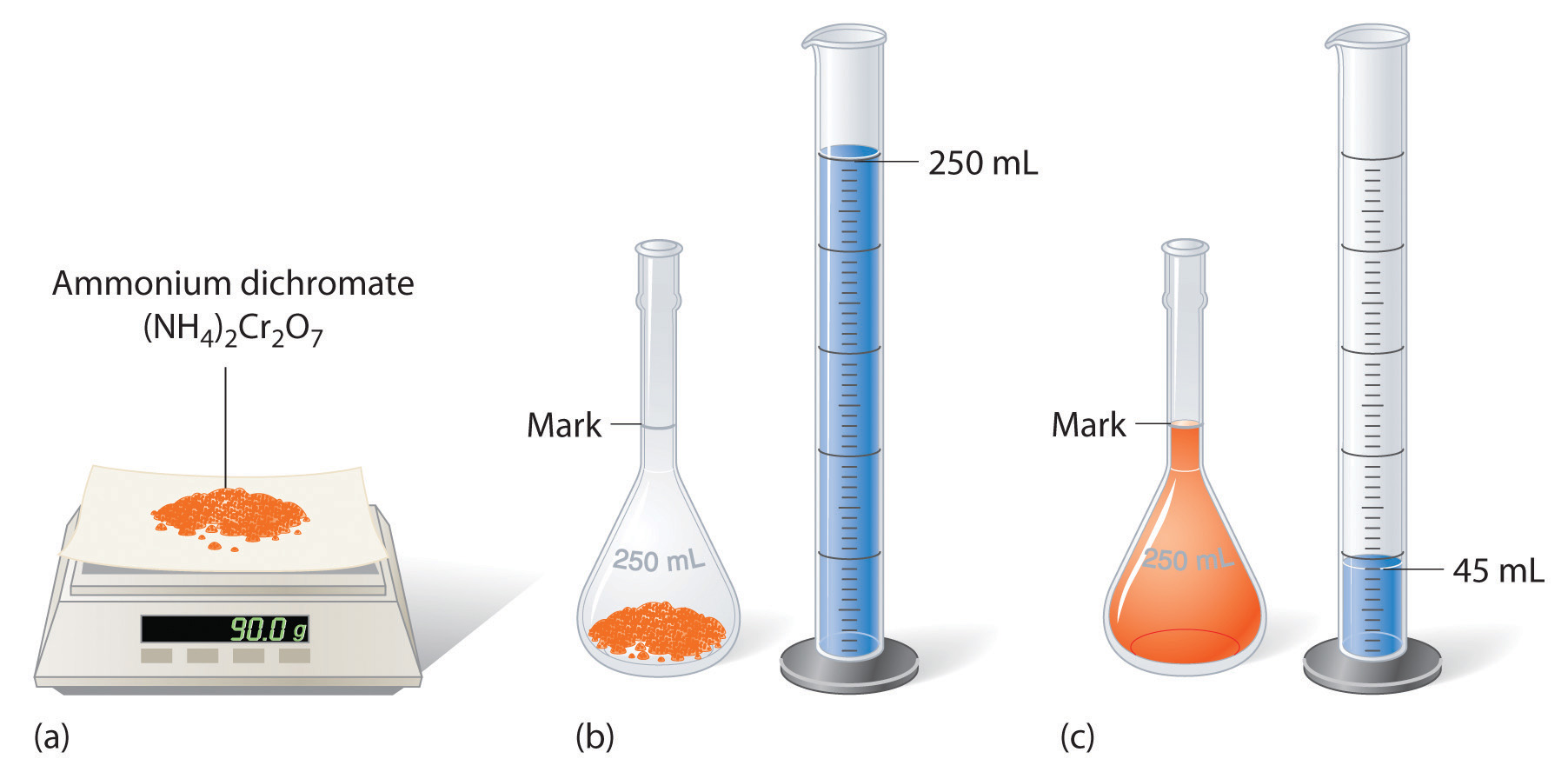
Figure 8.2.2 Preparation of 250 mL of a Solution of (NH4)2Cr2O7 in Water. The solute occupies space in the solution, so less than 250 mL of water are needed to make 250 mL of solution.
| Example 3 |
|---|
| The solution in Figure 8.2.1 contains 10.0 g of cobalt(II) chloride dihydrate, CoCl2•2H2O, in enough ethanol to make exactly 500 mL of solution. What is the molar concentration of CoCl2•2H2O? Given: mass of solute and volume of solution Asked for: concentration (M) Strategy: To find the number of moles of CoCl2•2H2O, divide the mass of the compound by its molar mass. Calculate the molarity of the solution by dividing the number of moles of solute by the volume of the solution in liters. Solution: The molar mass of CoCl2•2H2O is 165.87 g/mol. Therefore, \( moles\: CoCl_2 \cdot 2H_2O = \left( \dfrac{10.0 \: \cancel{g}} {165 .87\: \cancel{g} /mol} \right) = 0 .0603\: mol \) The volume of the solution in liters is \( volume = 500\: \cancel{mL} \left( \dfrac{1\: L} {1000\: \cancel{mL}} \right) = 0 .500\: L \) Molarity is the number of moles of solute per liter of solution, so the molarity of the solution is \( molarity = \dfrac{0.0603\: mol} {0.500\: L} = 0.121\: M = CoCl_2 \cdot H_2O \) |
| Exercise 3 |
|---|
| The solution shown in Figure 8.2.2 contains 90.0 g of (NH4)2Cr2O7 in enough water to give a final volume of exactly 250 mL. What is the molar concentration of ammonium dichromate? Answer: \((NH_4)_2Cr_2O_7 = 1.43\: M\) |
To prepare a particular volume of a solution that contains a specified concentration of a solute, we first need to calculate the number of moles of solute in the desired volume of solution using the relationship shown in Equation 8.2.2. We then convert the number of moles of solute to the corresponding mass of solute needed. This procedure is illustrated in Example 4.
| Example 4 |
|---|
| The so-called D5W solution used for the intravenous replacement of body fluids contains 0.310 M glucose. (D5W is an approximately 5% solution of dextrose [the medical name for glucose] in water.) Calculate the mass of glucose necessary to prepare a 500 mL pouch of D5W. Glucose has a molar mass of 180.16 g/mol. Given: molarity, volume, and molar mass of solute Asked for: mass of solute Strategy:
Solution: A We must first calculate the number of moles of glucose contained in 500 mL of a 0.310 M solution: \( V_L M_{mol/L} = moles \) \( 500\: \cancel{mL} \left( \dfrac{1\: \cancel{L}} {1000\: \cancel{mL}} \right) \left( \dfrac{0 .310\: mol\: glucose} {1\: \cancel{L}} \right) = 0 .155\: mol\: glucose \) B We then convert the number of moles of glucose to the required mass of glucose: \( mass \: of \: glucose = 0.155 \: \cancel{mol\: glucose} \left( \dfrac{180.16 \: g\: glucose} {1\: \cancel{mol\: glucose}} \right) = 27.9 \: g \: glucose \) |
| Exercise 4 |
|---|
| Another solution commonly used for intravenous injections is normal saline, a 0.16 M solution of sodium chloride in water. Calculate the mass of sodium chloride needed to prepare 250 mL of normal saline solution. Answer: 2.3 g NaCl |
A solution of a desired concentration can also be prepared by diluting a small volume of a more concentrated solution with additional solvent. A stock solution is a commercially prepared solution of known concentration and is a commercially prepared solution of known concentration, is often used for this purpose. Diluting a stock solution is preferred because the alternative method, weighing out tiny amounts of solute, is difficult to carry out with a high degree of accuracy. Dilution is also used to prepare solutions from substances that are sold as concentrated aqueous solutions, such as strong acids.
The procedure for preparing a solution of known concentration from a stock solution is shown in Figure 8.2.3. It requires calculating the number of moles of solute desired in the final volume of the more dilute solution and then calculating the volume of the stock solution that contains this amount of solute. Remember that diluting a given quantity of stock solution with solvent does not change the number of moles of solute present. The relationship between the volume and concentration of the stock solution and the volume and concentration of the desired diluted solution is therefore
\((V_s)(M_s) = moles\: of\: solute = (V_d)(M_d)\tag{8.2.4}\)
where the subscripts s and d indicate the stock and dilute solutions, respectively. Example 5 demonstrates the calculations involved in diluting a concentrated stock solution.
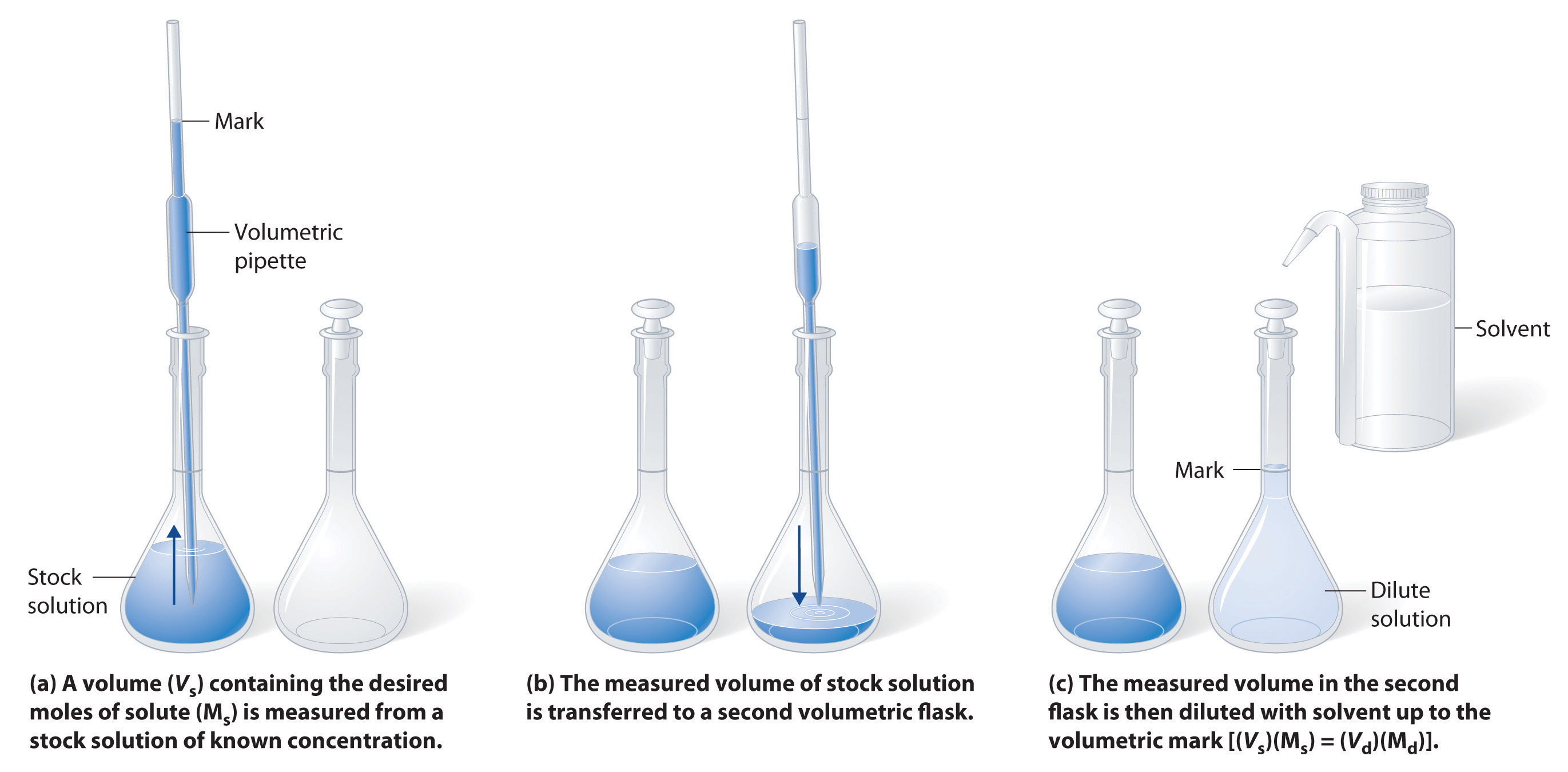
Figure 8.2.3 Preparation of a Solution of Known Concentration by Diluting a Stock Solution. (a) A volume (Vs) containing the desired moles of solute (Ms) is measured from a stock solution of known concentration. (b) The measured volume of stock solution is transferred to a second volumetric flask. (c) The measured volume in the second flask is then diluted with solvent up to the volumetric mark [(Vs)(Ms) = (Vd)(Md)].
| Example 1: 5 |
|---|
| What volume of a 3.00 M glucose stock solution is necessary to prepare 2500 mL of the D5W solution in Example 4? Given: volume and molarity of dilute solution Asked for: volume of stock solution Strategy: A Calculate the number of moles of glucose contained in the indicated volume of dilute solution by multiplying the volume of the solution by its molarity. B To determine the volume of stock solution needed, divide the number of moles of glucose by the molarity of the stock solution. Solution: A The D5W solution in Example 4 was 0.310 M glucose. We begin by using Equation 8.2.4 to calculate the number of moles of glucose contained in 2500 mL of the solution: \( moles\: glucose = 2500\: \cancel{mL} \left( \dfrac{1\: \cancel{L}} {1000\: \cancel{mL}} \right) \left( \dfrac{0 .310\: mol\: glucose} {1\: \cancel{L}} \right) = 0 .775\: mol\: glucose \) B We must now determine the volume of the 3.00 M stock solution that contains this amount of glucose: \( volume\: of\: stock\: soln = 0 .775\: \cancel{mol\: glucose} \left( \dfrac{1\: L} {3 .00\: \cancel{mol\: glucose}} \right) = 0 .258\: L\: or\: 258\: mL \) In determining the volume of stock solution that was needed, we had to divide the desired number of moles of glucose by the concentration of the stock solution to obtain the appropriate units. Also, the number of moles of solute in 258 mL of the stock solution is the same as the number of moles in 2500 mL of the more dilute solution; only the amount of solvent has changed. The answer we obtained makes sense: diluting the stock solution about tenfold increases its volume by about a factor of 10 (258 mL → 2500 mL). Consequently, the concentration of the solute must decrease by about a factor of 10, as it does (3.00 M → 0.310 M). We could also have solved this problem in a single step by solving Equation 8.2.4 for Vs and substituting the appropriate values: \( V_s = \dfrac{( V_d )(M_d )}{M_s} = \dfrac{(2 .500\: L)(0 .310\: \cancel{M} )} {3 .00\: \cancel{M}} = 0 .258\: L \) As we have noted, there is often more than one correct way to solve a problem. |
| Exercise 5 |
|---|
| What volume of a 5.0 M NaCl stock solution is necessary to prepare 500 mL of normal saline solution (0.16 M NaCl)? Answer: 16 mL |
Ion Concentrations in Solution
In Example 3, the concentration of a solution containing 90.00 g of ammonium dichromate in a final volume of 250 mL were calculated to be 1.43 M. Let’s consider in more detail exactly what that means. Ammonium dichromate is an ionic compound that contains two NH4+ ions and one Cr2O72− ion per formula unit. Like other ionic compounds, it is a strong electrolyte that dissociates in aqueous solution to give hydrated NH4+ and Cr2O72− ions:
\( (NH_4 )_2 Cr_2 O_7 (s) \xrightarrow {H_2 O(l)} 2NH_4^+ (aq) + Cr_2 O_7^{2-} (aq)\tag{8.2.5} \)
Thus 1 mol of ammonium dichromate formula units dissolves in water to produce 1 mol of Cr2O72− anions and 2 mol of NH4+ cations (see Figure 8.2.4).
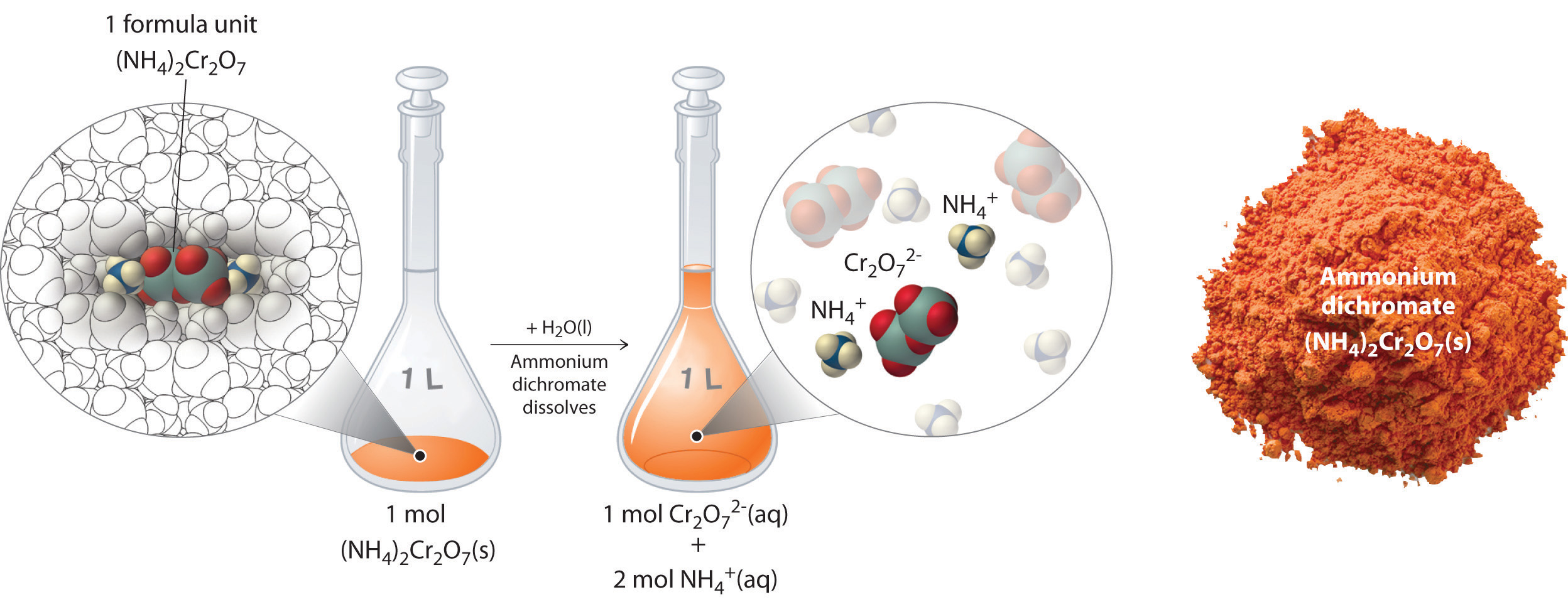
Figure 8.2.4 Dissolution of 1 mol of an Ionic Compound. In this case, dissolving 1 mol of (NH4)2Cr2O7 produces a solution that contains 1 mol of Cr2O72− ions and 2 mol of NH4+ ions. (Water molecules are omitted from a molecular view of the solution for clarity.)
When carrying out a chemical reaction using a solution of a salt such as ammonium dichromate, it is important to know the concentration of each ion present in the solution. If a solution contains 1.43 M (NH4)2Cr2O7, then the concentration of Cr2O72− must also be 1.43 M because there is one Cr2O72− ion per formula unit. However, there are two NH4+ ions per formula unit, so the concentration of NH4+ ions is 2 × 1.43 M = 2.86 M. Because each formula unit of (NH4)2Cr2O7 produces three ions when dissolved in water (2NH4+ + 1Cr2O72−), the total concentration of ions in the solution is 3 × 1.43 M = 4.29 M.
| Example 6 |
|---|
| What are the concentrations of all species derived from the solutes in these aqueous solutions?
Given: molarity Asked for: concentrations Strategy: A Classify each compound as either a strong electrolyte or a nonelectrolyte. B If the compound is a nonelectrolyte, its concentration is the same as the molarity of the solution. If the compound is a strong electrolyte, determine the number of each ion contained in one formula unit. Find the concentration of each species by multiplying the number of each ion by the molarity of the solution. Solution:
|
| Exercise 6 |
|---|
| What are the concentrations of all species derived from the solutes in these aqueous solutions?
 Answer:
|
Key Equations
definition of molarity
Equation 8.2.1: \( molarity = \dfrac{moles\: of\: solute}{liters\: of\: solution} = \dfrac{mmoles\: of\: solute} {milliliters\: of\: solution} \)
relationship among volume, molarity, and moles
Equation 8.2.2: \( V_L M_{mol/L} = \cancel{L} \left( \dfrac{mol}{\cancel{L}} \right) = moles \)
relationship between volume and concentration of stock and dilute solutions
Equation 8.2.4: \((V_s)(M_s) = moles\: of\: solute = (V_d)(M_d)\)
Summary
The concentration of a substance is the quantity of solute present in a given quantity of solution. Concentrations are usually expressed in terms of molarity, defined as the number of moles of solute in 1 L of solution. Solutions of known concentration can be prepared either by dissolving a known mass of solute in a solvent and diluting to a desired final volume or by diluting the appropriate volume of a more concentrated solution (a stock solution) to the desired final volume.
Key Takeaway
- Solution concentrations are typically expressed as molarities and can be prepared by dissolving a known mass of solute in a solvent or diluting a stock solution.
Conceptual Problems
-
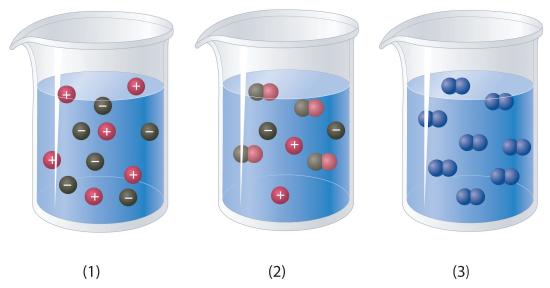
Which of the representations best corresponds to a 1 M aqueous solution of each compound? Justify your answers.
- NH3
- HF
- CH3CH2CH2OH
-
Na2SO4
-
Which of the representations shown in Problem 1 best corresponds to a 1 M aqueous solution of each compound? Justify your answers.
- CH3CO2H
- NaCl
- Na2S
- Na3PO4
- acetaldehyde
-
Would you expect a 1.0 M solution of CaCl2 to be a better conductor of electricity than a 1.0 M solution of NaCl? Why or why not?
-
An alternative way to define the concentration of a solution is molality, abbreviated m. Molality is defined as the number of moles of solute in 1 kg of solvent. How is this different from molarity? Would you expect a 1 M solution of sucrose to be more or less concentrated than a 1 m solution of sucrose? Explain your answer.
-
What are the advantages of using solutions for quantitative calculations?
Answer
-
-
-
-
-
If the amount of a substance required for a reaction is too small to be weighed accurately, the use of a solution of the substance, in which the solute is dispersed in a much larger mass of solvent, allows chemists to measure the quantity of the substance more accurately.
Numerical Problems
-
Calculate the number of grams of solute in 1.000 L of each solution.
- 0.2593 M NaBrO3
- 1.592 M KNO3
- 1.559 M acetic acid
- 0.943 M potassium iodate
-
Calculate the number of grams of solute in 1.000 L of each solution.
- 0.1065 M BaI2
- 1.135 M Na2SO4
- 1.428 M NH4Br
- 0.889 M sodium acetate
-
If all solutions contain the same solute, which solution contains the greater mass of solute?
- 1.40 L of a 0.334 M solution or 1.10 L of a 0.420 M solution
- 25.0 mL of a 0.134 M solution or 10.0 mL of a 0.295 M solution
- 250 mL of a 0.489 M solution or 150 mL of a 0.769 M solution
-
Complete the following table for 500 mL of solution.
Compound Mass (g) Moles Concentration (M) calcium sulfate 4.86 acetic acid 3.62 hydrogen iodide dihydrate 1.273 barium bromide 3.92 glucose 0.983 sodium acetate 2.42 -
What is the concentration of each species present in the following aqueous solutions?
- 0.489 mol of NiSO4 in 600 mL of solution
- 1.045 mol of magnesium bromide in 500 mL of solution
- 0.146 mol of glucose in 800 mL of solution
- 0.479 mol of CeCl3 in 700 mL of solution
-
What is the concentration of each species present in the following aqueous solutions?
- 0.324 mol of K2MoO4 in 250 mL of solution
- 0.528 mol of potassium formate in 300 mL of solution
- 0.477 mol of KClO3 in 900 mL of solution
- 0.378 mol of potassium iodide in 750 mL of solution
-
What is the molar concentration of each solution?
- 8.7 g of calcium bromide in 250 mL of solution
- 9.8 g of lithium sulfate in 300 mL of solution
- 12.4 g of sucrose (C12H22O11) in 750 mL of solution
- 14.2 g of iron(III) nitrate hexahydrate in 300 mL of solution
-
What is the molar concentration of each solution?
- 12.8 g of sodium hydrogen sulfate in 400 mL of solution
- 7.5 g of potassium hydrogen phosphate in 250 mL of solution
- 11.4 g of barium chloride in 350 mL of solution
- 4.3 g of tartaric acid (C4H6O6) in 250 mL of solution
-
Give the concentration of each reactant in the following equations, assuming 20.0 g of each and a solution volume of 250 mL for each reactant.
- BaCl2(aq) + Na2SO4(aq) →
- Ca(OH)2(aq) + H3PO4(aq) →
- Al(NO3)3(aq) + H2SO4(aq) →
- Pb(NO3)2(aq) + CuSO4(aq) →
- Al(CH3CO2)3(aq) + NaOH(aq) →
-
An experiment required 200.0 mL of a 0.330 M solution of Na2CrO4. A stock solution of Na2CrO4 containing 20.0% solute by mass with a density of 1.19 g/cm3 was used to prepare this solution. Describe how to prepare 200.0 mL of a 0.330 M solution of Na2CrO4 using the stock solution.
-
Calcium hypochlorite [Ca(OCl)2] is an effective disinfectant for clothing and bedding. If a solution has a Ca(OCl)2 concentration of 3.4 g per 100 mL of solution, what is the molarity of hypochlorite?
-
Phenol (C6H5OH) is often used as an antiseptic in mouthwashes and throat lozenges. If a mouthwash has a phenol concentration of 1.5 g per 100 mL of solution, what is the molarity of phenol?
-
If a tablet containing 100 mg of caffeine (C8H10N4O2) is dissolved in water to give 10.0 oz of solution, what is the molar concentration of caffeine in the solution?
-
A certain drug label carries instructions to add 10.0 mL of sterile water, stating that each milliliter of the resulting solution will contain 0.500 g of medication. If a patient has a prescribed dose of 900.0 mg, how many milliliters of the solution should be administered?
Answers
-
-
-
-
-
-
-
-
-
-
-
0.48 M ClO−
-
-
1.74 × 10−3 M caffeine
Contributors
Modified by Joshua Halpern (Howard University)

