CA6. Cyclic Systems
- Page ID
- 4045
Cyclic systems are a little different from open-chain systems. In an open chain, any bond can be rotated 360 degrees, going through many different conformations. That complete rotation isn't possible in a cyclic system, because the parts that you would be trying to twist away from each other would still be connected together. Cyclic systems have fewer "degrees of freedom" than aliphatic systems; they have "restricted rotation".
Because of the restricted rotation of cyclic systems, most of them have much more well-defined shapes than their aliphatic counterparts. Let's take a look at the basic shapes of some common rings. Many biologically important compounds are built around structures containing rings, so it's important that we become familiar with them. In nature, three- to six-membered rings are frequently encountered, so we'll focus on those.
Cyclopropane
A three membered ring has no rotational freedom whatsoever. A plane is defined by three points, so the three carbon atoms in cyclopropane are all constrained to lie in the same plane.
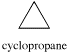
Furthermore, if you look at a model you will find that the neighboring C-H bonds (C-C bonds, too) are all held in eclipsed conformations. Cyclopropane is always at maximum torsional strain. This strain can be illustrated in a line drawing of cyclopropane as shown from the side. In this oblique view, the dark lines mean that those sides of the ring are closer to you.
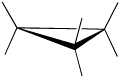
However, the ring isn't big enough to introduce any steric strain, which does not become a factor until we reach six membered rings. Until that point, rings are not flexible enough for two atoms to reach around and bump into each other. The really big problem with cyclopropane is that the C-C-C bond angles are all too small.
- All the carbon atoms in cyclopropane appear to be tetrahedral.
- These bond angles ought to be 109 degrees.
- The angles in an equilateral triangle are actually 60 degrees, about half as large as the optimum angle.
- This factor introduces a huge amount of strain in the molecule, called ring strain.
Cyclobutane
Cyclobutane is a four membered ring. In two dimensions, it is a square, with 90 degree angles at each corner.

However, in three dimensions, cyclobutane is flexible enough to buckle into a "butterfly" shape, relieving torsional strain a little bit. When it does that, the bond angles get a little worse, going from 90 degrees to 88 degrees. In a line drawing, this butterfly shape is usually shown from the side, with the near edges drawn using darker lines.
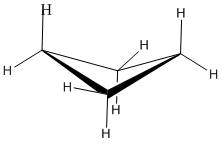
- With bond angles of 88 rather than 109 degrees, cyclobutane has a lot of ring strain, but less than in cyclopropane.
- Torsional strain is still present, but the neighboring bonds are not exactly eclipsed in the butterfly.
- Cyclobutane is still not large enough that the molecule can reach around to cause crowding. Steric strain is very low.
- Cyclobutanes are a little more stable than cyclopropanes and are also a little more common in nature.
Cyclopentanes
Cyclopentanes are even more stable than cyclobutanes, and they are the second-most common paraffinic ring in nature, after cyclohexanes. In two dimensions, a cyclopentane appears to be a regular pentagon.
In three dimensions, there is enough freedom of rotation to allow a slight twist out of this planar shape. In a line drawing, this three-dimensional shape is drawn from an oblique view, just like cyclobutane.
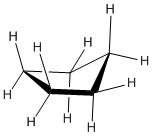
The ideal angle in a regular pentagon is about 107 degrees, very close to a tetrahedral bond angle. Cyclopentane distorts only very slightly into an "envelope" shape in which one corner of the pentagon is lifted up above the plane of the other four, and as a result, ring strain is entirely removed. The envelope removes torsional strain along the sides and flap of the envelope. However, the neighbouring carbons are eclipsed along the "bottom" of the envelope, away from the flap. There is still some torsional strain in cyclopentane. Again, there is no steric strain in this system.


