Answers to Chapter 07 Study Questions

Last updated
Save as PDF

Page ID: 11896

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\(\mathrm{\lambda\nu=c}\); \(\mathrm{\nu = 7.5 \times 10^{11}\: MHz\times\dfrac{10^6\:Hz}{1\:MHz}=7.5 \times 10^{17}\: Hz =7.5 \times 10^{17}\: s^{-1}}\)

\(\mathrm{\lambda =\dfrac{c}{\nu}= \dfrac{2.9979\times10^8\:m/s}{7.5\times10^{17}\:s^{-1}}=4.0\times10^{-10}\:m\times\dfrac{10^9\:nm}{1\:m}=0.40\:nm}\)

1. \(\mathrm{\Delta E = E_2 - E_1}\); \(\mathrm{E(n) = \dfrac{-R}{n^2}}\); \(\mathrm{R = 2.178 \times 10^{-18}\: J}\)
  \(\mathrm{E_1 = \dfrac{-2.178 \times 10^{-18} J}{3^2} = \dfrac{-2.178 \times 10^{-18}\: J}{9} = -2.420 \times 10^{-19}\: J}\)
  \(\mathrm{E_2 =\dfrac{-2.178 \times 10^{-18}\: J}{2^2} = \dfrac{-2.178 \times 10^{-18}\: J}{4} = -5.445 \times 10^{-19}\: J}\)
  \(\mathrm{\Delta E = E_2 - E_1 = -5.445 \times 10^{-19}\: J - (-2.420 \times 10^{-19}\: J) = -3.025 \times 10^{-19}\: J}\)
2. \(\mathrm{\lambda \nu = c}\); \(\mathrm{\Delta E = h\nu}\); \(\mathrm{\lambda = \dfrac{hc}{\Delta E}}\) where \(\mathrm{c = 2.9979 \times 10^8\: m/s}\), \(\mathrm{h = 6.626 \times 10^{-34}\: J\cdot s}\)
  \(\mathrm{\lambda =\dfrac{hc}{\Delta E}=\dfrac{(6.626\times10^{-34}\:J\:s)(2.998\times10^8\:m/s)}{3.025\times10^{-19}\:J}= 6.567 \times 10^{-7}\: m =656.7\: nm}\)

The new idea in Bohr's model was that electrons can only exist in specific energy states. Bohr's model included an electron orbiting the nucleus as a planet does the sun; according to the quantum mechanical model, we can only define the probability of finding an electron at a given location. When electrons drop from higher energy levels to lower ones, they give off energy in the form of light. The color of light emitted depends on the energy difference between the levels. The greater the energy difference, the shorter the wavelength of light, the more violet the color.

The electron configurations of all Group 1 metals end with a single s electron. When these metals lose this s electron, they acquire noble gas electron configurations which end in completed energy levels. They have a strong tendency, therefore, to lose their final single s electrons. This makes them extremely reactive and the metals with the greatest tendency to lose electrons. Group 17 elements need only 1 p electron to complete their outermost energy levels. They have a strong tendency to gain an electron and thus are the most reactive nonmetals. The energy levels of noble gases are all full so these elements have no need to gain or lose electrons and therefore don't react with anything.

1. \(\mathrm{2n^2}\), where \(\mathrm{n = Principal\: Energy\: level}\)
2. \(\mathrm{s = 2\: e^-}\), \(\mathrm{p = 6\: e^-}\), \(\mathrm{d = 10\: e^-}\), \(\mathrm{f = 14\: e^-}\)
3. \(\mathrm{2\: e^-}\)

Does not exist: c) 2d; Increasing energy: 1s < 2s < 3d < 4p < 4f

1. 2 e^- (it’s a 2p orbital)
2. 2 e^- (it’s a 1s sublevel)
3. 1 e^- (it includes all 4 quantum #’s)

1. s
2. d
3. p
4. f

1. ground state
2. impossible
3. excited
4. excited

1. 1s²2s²2p⁶3s²3p⁴
2. 1s²2s²2p⁶3s²3p⁶4s²3d⁷
3. 1s²2s²2p⁶3s²3p⁶4s²3d¹⁰4p⁶5s²

1. \(\ce{Ba}\) (Period 6, Group 2)
2. \(\ce{He}\) (1s²)
3. \(\ce{As}\) (4s²4p³ = Period 4, Group 15)
4. \(\ce{C}\) (2s²2p² = Period 2, Group 14)
5. \(\ce{Cl}\) (Period 3, Group 17)
6. \(\ce{Mn}\) (3d⁵ = 5th transition metal where 3d is being filled) and also \(\ce{Cr}\) (which is 4s¹3d⁵)

1. \(\mathrm{[_{86}Rn]}\) 7s²5f⁷ (note that the total number of electrons is equal to 95)
2. for a 5f electron: \(\mathrm{n = 5}\), \(\mathrm{l = 3}\), \(\mathrm{m_{\, \large l} = -3}\), \(\mathrm{m_{\, \large s} = -\dfrac{1}{2}}\) (\(\mathrm{m_{\, \large l} = -3\: to\: 3}\), \(\mathrm{m_{\, \large s} = +\dfrac{1}{2}\: or\: -\dfrac{1}{2}}\))

s: p:

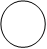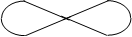As n increases, the size of an orbital increases since the probability of finding an electron farther from the nucleus increases.

1. \(\textrm{O:}\:\:\underset{\large{1s}}{(\uparrow\downarrow)}\:\:\:\underset{\large{2s}}{(\uparrow\downarrow)}\:\:\:\underset{\large{2p}}{(\uparrow\downarrow)(\uparrow\:)(\uparrow\:)}\)
2. \(\textrm{Ti:}\:\:\underset{\large{1s}}{(\uparrow\downarrow)}\:\:\:\underset{\large{2s}}{(\uparrow\downarrow)}\:\:\:\underset{\large{2p}}{(\uparrow\downarrow)(\uparrow\downarrow)(\uparrow\downarrow)}\:\:\:\underset{\large{3s}}{(\uparrow\downarrow)}\:\:\:\underset{\large{3p}}{(\uparrow\downarrow)(\uparrow\downarrow)(\uparrow\downarrow)}\:\:\:\underset{\large{4s}}{(\uparrow\downarrow)}\:\:\:\underset{\large{3d}}{(\uparrow\:)(\uparrow\:)(\:\:)(\:\:)(\:\:)}\)

1. \(\ce{Ar}\); \(\ce{Na}\)
2. \(\ce{Ca}\); \(\ce{S}\)