5A: Free Particles

The simplest system in quantum mechanics has the potential energy \(V=0\) everywhere. This is called a free particle since it has no forces acting on it. We consider the one-dimensional case, with motion only in the \(x\)-direction, giving the Schrödinger equation

\[- \dfrac{\hbar^{2}}{2m}\dfrac{d^{2}\psi (x)}{dx^2}= E\psi (x)\label{5P.1}\]

Ordinary derivatives can be used since there is one independent variable. The equation simplifies to a 1-D classical wave equation:

\[\psi {}'' (x)+k^{2}\psi (x)=0\label{5P.2}\]

with the definition

\[k^2 \equiv 2mE/\hbar^2\label{5P.3}\]

Possible solutions of Equation \(\ref{5P.2}\) are

\[\psi (x)= const\begin{Bmatrix}
\sin(kx)\\
\cos(kx)\\
e^{\pm ikx}\end{Bmatrix}\label{5P.4}\]

There is no restriction on the value of \(k\). Thus a free particle, even in quantum mechanics, can have any non-negative value of the energy (which is all kinetic energy in this case)

\[E=\dfrac{\hbar^2k^2}{2m}\geq 0\label{5P.5}\]

The energy levels in this case are not quantized and correspond to the same continuum of kinetic energy shown by a classical particle. It is of interest also to consider the x-component of linear momentum for the free-particle solutions. The eigenvalue equation for momentum should read

\[\hat{p}_{x}\psi (x)=-i\hbar\dfrac{d\psi (x)}{dx}=p\psi (x)\label{5P.6}\]

where we have denoted the momentum eigenvalue as p. It is easily shown that neither of the functions sin kx or cos kx from (4) is an eigenfunction of \( \hat{p}_{x}\). But \(e^{\pm ikx}\) are both eigenfunctions with eigenvalues \(p=\pm\hbar k\), respectively. Evidently the momentum p can take on any real value between -\(\infty\) and +\(\infty\). The kinetic energy, equal to \(E=p^2/2m\), can correspondingly have any value between 0 and +\(\infty\).

The energy levels of a free particle are not quantized and correspond to the same continuum of kinetic energies shown by a classical particle.

The functions \(\sin \;kx\) and \(\cos\; kx\), while not eigenfunctions of \(\hat{p}_{x}\), are each superpositions of the two eigenfunctions \(e^{\pm ikx}\), by virtue of the trigonometric identities

\[\cos (kx)=\dfrac{1}{2}(e^{ikx} +e^{-ikx}) \label{5P.7}\]

and

\[\sin(kx)= \dfrac{1}{2i}(e^{ikx} -e^{-ikx})\label{5P.8}\]

The eigenfunction \(e^{ikx}\) for k > 0 represents the particle moving from left to right on the x-axis, with momentum p > 0. Correspondingly, \(e^{-ikx}\) represents motion from right to left with p < 0. The functions sin (kx) and cos (kx​) represent standing waves, obtained by superposition of opposing wave motions. Although these latter two are not eigenfunctions of \(\hat{p}_{x}\) but are eigenfunctions of \(\hat{p}^2_{x}\), hence of the Hamiltonian \(\hat{H}\).

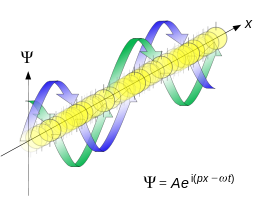
Figure \(\PageIndex{1}\): Propagation of de Broglie waves in 1d - real part of the complex amplitude is blue, imaginary part is green. The probability (shown as the colour opacity) of finding the particle at a given point x is spread out like a waveform, there is no definite position of the particle. Image used with permission from Wikipedia.