Uncertainty Principle
- Page ID
- 1654
In classical physics, studying the behavior of a physical system is often a simple task due to the fact that several physical qualities can be measured simultaneously. However, this possibility is absent in the quantum world. In 1927 the German physicist Werner Heisenberg described such limitations as the Heisenberg Uncertainty Principle, or simply the Uncertainty Principle, stating that it is not possible to measure both the momentum and position of a particle simultaneously.
The Nature of Measurement
In order to understand the conceptual background of the Heisenberg Uncertainty Principle it is important to understand how physical values are measured. In almost any measurement that is made, light is reflected off the object that is being measured and processed. The shorter the wavelength of light used, or the higher its frequency and energy, the more accurate the results. For example, when attempting to measure the speed of a tennis ball as it is dropped off of a ledge, photons(measurement of light) are shot off the tennis ball, reflected, and then processed by certain equipment. Because the tennis ball is so large compared to the photons, it is unaffected by the efforts of the observer to measure its physical quantities. However, if a photon is shot at an electron, the minuscule size of the electron and its unique wave-particle duality introduces consequences that can be ignored when taking measurements of macroscopic objects.
Heisenberg himself encountered such limitations as he attempted to measure the position of an electron with a microscope. As noted, the accuracy of any measurement is limited by the wavelength of light illuminating the electron. Therefore, in principle, one can determine the position as accurately as one wishes by using light of very high frequency, or short wave-lengths. However, the collision between such high energy photons of light with the extremely small electron causes the momentum of the electron to be disturbed.
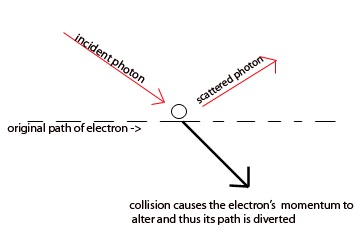
Thus, increasing the energy of the light (and increasing the accuracy of the electron's position measurement), increases such a deviation in momentum. Conversely, if a photon has low energy the collision does not disturb the electron, yet the position cannot be accurately determined. Heisenberg concluded in his famous 1927 paper on the topic,
"At the instant of time when the position is determined, that is, at the instant when the photon is scattered by the electron, the electron undergoes a discontinuous change in momentum. This change is the greater the smaller the wavelength of the light employed, i.e., the more exact the determination of the position. At the instant at which the position of the electron is known, its momentum therefore can be known only up to magnitudes which correspond to that discontinuous change; thus, the more precisely the position is determined, the less precisely the momentum is known..." (Heisenberg, 1927, p. 174-5).
Heisenberg realized that since both light and particle energy are quantized, or can only exist in discrete energy units, there are limits as to how small, or insignificant, such an uncertainty can be. As proved later in this text, that bound ends up being expressed by Planck's Constant, h = 6.626*10-34 J*s.
It is important to mention that The Heisenberg Principle should not be confused with the observer effect. The observer effect is generally accepted to mean that the act of observing a system will influence that which is being observed. While this is important in understanding the Heisenberg Uncertainty Principle, the two are not interchangeable. The error in such thinking can be explained using the wave-particle duality of electromagnetic waves, an idea first proposed by Louis de Broglie. Wave-particle duality asserts that any energy exhibits both particle- and wave-like behavior. As a consequence, in quantum mechanics, a particle cannot have both a definite position and momentum. Thus, the limitations described by Heisenberg are a natural occurrence and have nothing to do with any limitations of the observational system.
Heisenberg’s Uncertainty Principle
It is mathematically possible to express the uncertainty that, Heisenberg concluded, always exists if one attempts to measure the momentum and position of particles.First, we must define the variable “x” as the position of the particle, and define “p” as the momentum of the particle. The momentum of a photon of light is known to simply be its frequency, expressed by the ratio h/λ, where h represents Planck’s constant and λ represents the wavelength of the photon. The position of a photon of light is simply its wavelength, \lambda\).. In order to represent finite change in quantities, the Greek uppercase letter delta, or Δ, is placed in front of the quantity. Therefore,
\[\Delta{p}=\dfrac{h}{\lambda}\]
\[\Delta{x}= \lambda\]
By substituting \(\Delta{x}\) for \(\lambda\) in the first equation, we derive
\[\Delta{p}=\dfrac{h}{\Delta{x}}\]
or,
\[\Delta{p}\Delta{x}=h\]
Note, we can derive the same formula by assuming the particle of interest is behaving as a particle, and not as a wave. Simply let Δp=mu, and Δx=h/mu (from De Broglie’s expression for the wavelength of a particle). Substituting in Δp for mu in the second equation leads to the very same equation derived above-ΔpΔx=h. This equation was refined by Heisenberg and his colleague Niels Bohr, and was eventually rewritten as
\[\Delta{p}\Delta{x} \ge \dfrac{h}{4\pi}\]
What this equation reveals is that the more accurately a particle’s position is known, or the smaller Δx is, the less accurately the momentum of the particle Δp is known. Mathematically, this occurs because the smaller Δx becomes, the larger Δp must become in order to satisfy the inequality. However, the more accurately momentum is known the less accurately position is known.
Understanding the Uncertainty Principle through Wave Packets and the Slit Experiment
It is hard for most people to accept the uncertainty principle, because in classical physics the velocity and position of an object can be calculated with certainty and accuracy. However, in quantum mechanics, the wave-particle duality of electrons does not allow us to accurately calculate both the momentum and position because the wave is not in one exact location but is spread out over space. A "wave packet" can be used to demonstrate how either the momentum or position of a particle can be precisely calculated, but not both of them simultaneously. An accumulation of waves of varying wavelengths can be combined to create an average wavelength through an interference pattern: this average wavelength is called the "wave packet". The more waves that are combined in the "wave packet", the more precise the position of the particle becomes and the more uncertain the momentum becomes because more wavelengths of varying momenta are added. Conversely, if we want a more precise momentum, we would add less wavelengths to the "wave packet" and then the position would become more uncertain. Therefore, there is no way to find both the position and momentum of a particle simultaneously.
Several scientists have debated the Uncertainty Principle, including Einstein. Einstein created a slit experiment to try and disprove the Uncertainty Principle. He had light passing through a slit, which causes an uncertainty of momentum because the light behaves like a particle and a wave as it passes through the slit. Therefore, the momentum is unknown, but the initial position of the particle is known. Here is a video that demonstrates particles of light passing through a slit and as the slit becomes smaller, the final possible array of directions of the particles becomes wider. As the position of the particle becomes more precise when the slit is narrowed, the direction, or therefore the momentum, of the particle becomes less known as seen by a wider horizontal distribution of the light.
The Importance of the Heisenberg Uncertainty Principle
Heisenberg’s Uncertainty Principle not only helped shape the new school of thought known today as quantum mechanics, but it also helped discredit older theories. Most importantly, the Heisenberg Uncertainty Principle made it obvious that there was a fundamental error in the Bohr model of the atom. Since the position and momentum of a particle cannot be known simultaneously, Bohr’s theory that the electron traveled in a circular path of a fixed radius orbiting the nucleus was obsolete. Furthermore, Heisenberg’s uncertainty principle, when combined with other revolutionary theories in quantum mechanics, helped shape wave mechanics and the current scientific understanding of the atom.
References
- Petrucci, Ralph H., William S. Harwood, F. Geoffrey Herring, and Jeffry D. Madura. General Chemistry. Principles and Modern Applications. 9th ed. Upper Saddle River, NJ: Pearson Prentice Hall, 2007. 298-299. Print.
- Zumdahl, Stephen S., and Susan Zumdahl. Chemistry. 5th ed. . Boston, MA: Houghton Mifflin Harcourt, 1999. 307-08. Print
- Heisenberg, W. (1927), "Über den anschaulichen Inhalt der quantentheoretischen Kinematik und Mechanik", Zeitschrift für Physik . English translation: J. A. Wheeler and H. Zurek,Quantum Theory and Measurement Princeton Univ. Press, 1983, pp. 174–5.
Outside Links
- http://en.Wikipedia.org/wiki/Uncertainty_principle
- http://plato.stanford.edu/entries/qt-uncertainty/
- http://farside.ph.utexas.edu/teachin...es/node26.html
- www.marts100.com/hup.htm
- http://en.wikibooks.org/wiki/Quantum...inty_Principle
- www.youtube.com/watch?v=KT7xJ0tjB4A
Problems
- What aspect of the Bohr model of the atom does the Heisenberg Uncertainty Principle discredit?
- What is the difference between the Heisenberg Uncertainty Principle and the Observer Effect?
- A Hydrogen atom has a radius of 0.05nm with a position accuracy of 1.0%. What is the uncertainty in determining the velocity?
- What is the uncertainty in the speed of a beam of electrons whose position is known with an uncertainty of 10 nm?
- Using the Uncertainty Principle, find the radius of an atom (in nm) that has an electron with a position accuracy of 3.0% and a known velocity of \(2\times 10^9\, m/s\).
Answers:
1.) The Heisenberg Uncertainty Principle discredits the aspect of the Bohr atom model that an electron is constrained to a one-dimensional orbit of a fixed radius around the nucleus.
2.) The Observer Effect means the act of observing a system will influence what is being observed, whereas the Heisenberg Uncertainty Principle has nothing to do with the observer or equipment used during observation. It simply states that a particle behaves both as a wave and a particle and therefore cannot have both a definite momentum and position.
3.) Uncertainty principle: ΔxΔp≥h/4Π
Can be written (x)(m)(v)(%)=h/4Π
(position)(mass of electron)(velocity)(percent accuracy)=(Plank's Constant)/4Π
(.05*10-9 m)(9.11*10-31 kg)(v)(.01)=(6.626*10-34 J*s)/4Π
v=1*108 m/s
4.) Uncertainty principle: ΔxΔp≥h/4Π
(10*10-9 m)(Δp)≥(6.626*10-34 J*s)/4Π
Δp≥5*10-26 (kg*m)/s
5.) Uncertainty principle: ΔxΔp≥h/4Π
Can be written (x)(m)(v)(%)=h/4Π
(position)(mass of electron)(velocity)(percent accuracy)=h/4Π
(radius)(9.11*10-31 kg)(2*109)(.03)=(6.626*10-34 J*s)/4Π
r=9*10-12 m
r=9*10-3 nm

