Capillary Action
- Page ID
- 1500
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
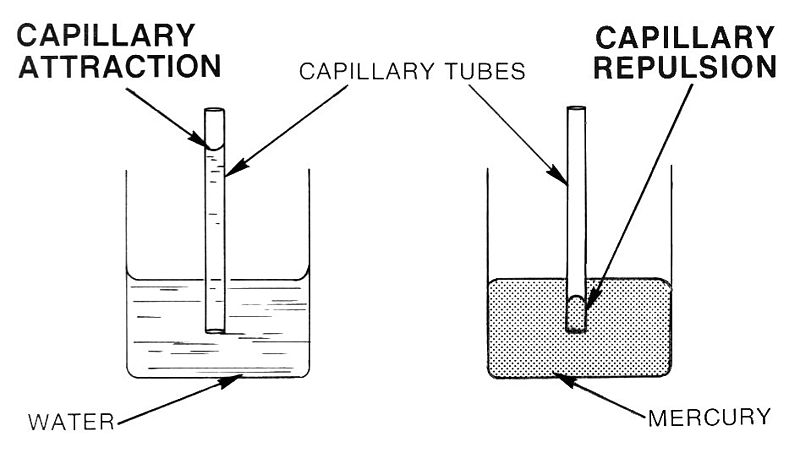
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Capillary action can be defined as the ascension of liquids through slim tube, cylinder or permeable substance due to adhesive and cohesive forces interacting between the liquid and the surface. When intermolecular bonding of a liquid itself is substantially inferior to a substances’ surface it is interacting, capillarity occurs. Also, the diameter of the container as well as the gravitational forces will determine amount of liquid raised. While, water possesses this unique property, a liquid like mercury will not display the same attributes due to the fact that it has higher cohesive force than adhesive force.
Forces in Capillary Action
Three main variables that determine whether a liquid possesses capillary action are:
- Cohesive force: It is the intermolecular bonding of a substance where its mutual attractiveness forces them to maintain a certain shape of the liquid.
- Surface tension: This occurs as a result of like molecules, cohesive forces, banding together to form a somewhat impenetrable surface on the body of water. The surface tension is measured in Newton/meter.
- Adhesive force: When forces of attraction between unlike molecules occur, it is called adhesive forces.
Capillary action only occurs when the adhesive forces are stronger than the cohesive forces, which invariably becomes surface tension, in the liquid.
.jpg?revision=1&size=bestfit&width=487&height=276)
A good way to remember the difference between adhesive and cohesive forces is that with adhesive forces you add another set of molecules, the molecules of the surface, for the liquid to bond with. With cohesive forces, the molecules of the liquid will only cooperate with their own kind. Decreased surface tension also increases capillary action. This is because decreased surface tension means that the intermolecular forces are decreased, thus decreasing cohesive forces. As a result, capillary action will be even greater.
Applications
Practical use of capillary action is evident in all forms of our daily lives. It makes performing our tasks efficiently and effectively. Some applications of this unique property include:
- The fundamental properties are used to absorb water by using paper towels. The cohesive and adhesive properties draw the fluid into the paper towel. The liquid flows into the paper towel at a certain rate.
- A technique called thin layer chromatography uses capillary action in which a layer of liquid is used to separate mixtures from substances.
- Capillary action helps us naturally by pumping out tear fluid in the eye. This process cleanses the eye and clears all of the dust and particles that are around the ducts of the eye.
- To generate energy: A possible use for capillary action is as a source of renewable energy. By allowing water to climb through capillaries, evaporate once it reaches the top, the condensate and drop back down to the bottom spinning a turbine on its way to create the energy, capillary action can make electricity! Although this idea is still in the works, it goes to show the potential that capillary action holds and how important it is.

When measuring the level of liquid of a test tube or buret, it is imperative to measure at the meniscus line for an accurate reading. It is possible to measure the height (represented by h) of a test tube, buret, or other liquid column using the formula:
\[ h = \dfrac{2\gamma \cos\theta}{\rho\;g\;r} \]
In this formula,
- γ represents the surface tension in a liquid-air environment,
- θ is the angle of contact or the degree of contact,
- ρ is the density of the liquid in the representative column,
- g is the acceleration due to the force of gravity and
- r is the radius of the tube in which the liquid is presented in.
At optimum level, in which a glass tube filled with water is present in air, this formula can determine the height of a specific column of water in meters (m):
\[ h\approx\dfrac{1.4 \times 10^{-5}}{r}\]
However, the following conditions must be met for this formula to occur.
- γ= 0.0728 N/m (when water is at a temperature of 20°C)
- θ= 20°
- ρis 1000 kg/m3
- g= 9.8 m/s2
Formula for Volume of Liquid Transport in Medium:
When certain objects that are porous encounter a liquid medium, it will begin to absorb the liquid at a rate which actually decreases over a period of time. This formula is written as:
\[ V = S*A\sqrt{t} \]
In this specific formula,
- A is the wet area (cross-section),
- S is the sorptivity (capacity of medium to absorb using the process of capillary action),
- V is the volume of liquid absorbed in time, t.
Questions
- Name one way to increase capillary action, and one way to decrease it.
- If cohesion is greater than adhesion, will the meniscus be convex or concave?
- What would be the height of a liquid in a column, on earth, with a liquid-air surface tension 0f .0973 N/m, contact angle of 30 degrees, density of 1200 kg/m3? Note that the radius of the tube is 0.2 meters.
- What would be the height of water in a glass tube with a radius of .6mm?
Solutions
- Increase capillary action: Increase temperature, decrease capillary tube diameter, perform any number of actions to decrease surface tension, etc…! Decrease capillary action: The opposite of the steps you would take to increase, also, increasing the density of the liquid you're working with.
- The meniscus will result in a convex formation.
- Using the formula above, the height of the liquid will be 7.165* 10-5m high.
- Using the formula above, the height of the water in the glass tube would be .014m high.
References
- Petrucci, Ralph, and William Harwood. F. Geoffrey Herring. Jeffry Madura. General Chemistry: Principles and Modern Applications. 9th ed. Upper Saddle River, NJ: Pearson, 2007.
- Cyclical Gravity Greenhouse Liquid Capillary Action Energy Generator, R Smith, 9.11.2005 14:38,
- Capillary Action, Wikipedia
- Capillary Action, from USGS Water Science for Schools." USGS Georgia Water Science Center - Home Page. Web. 04 June 2011.
Contributors and Attributions
- Achille Peiris, Becky Stein

