8.4: Magnetic Properties and the Zeeman Effect
- Page ID
- 4522
Magnetism results from the circular motion of charged particles. This property is demonstrated on a macroscopic scale by making an electromagnet from a coil of wire and a battery. Electrons moving through the coil produce a magnetic field (Figure \(\PageIndex{1}\)), which can be thought of as originating from a magnetic dipole or a bar magnet.
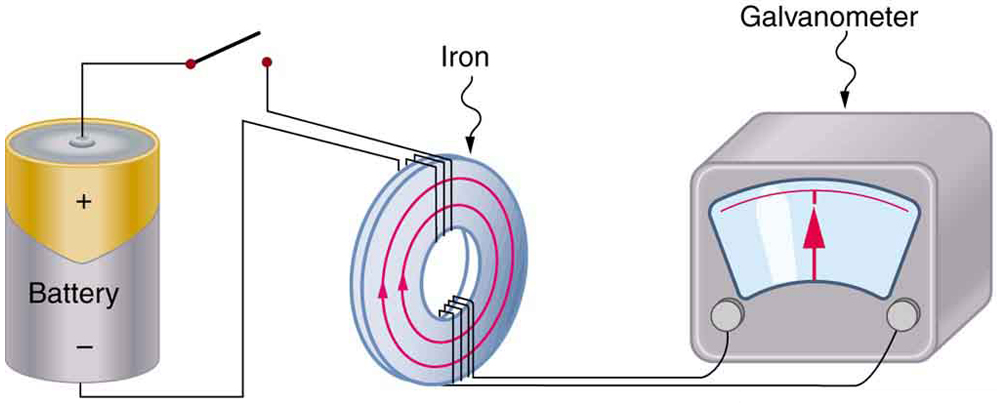
Magnetism results from the circular motion of charged particles.
Electrons in atoms also are moving charges with angular momentum so they too produce a magnetic dipole, which is why some materials are magnetic. A magnetic dipole interacts with an applied magnetic field, and the energy of this interaction is given by the scalar product of the magnetic dipole moment, and the magnetic field, \(\vec{B}\).
\[E_B = - \vec{\mu} _m \cdot \vec{B} \label {8.4.1}\]
Magnets are acted on by forces and torques when placed within an external applied magnetic field (Figure \(\PageIndex{2}\)). In a uniform external field, a magnet experiences no net force, but a net torque. The torque tries to align the magnetic moment (\(\vec{\mu} _m\) of the magnet with the external field \(\vec{B}\). The magnetic moment of a magnet points from its south pole to its north pole.

In a non-uniform magnetic field a current loop, and therefore a magnet, experiences a net force, which tries to pull an aligned dipole into regions where the magnitude of the magnetic field is larger and push an anti-aligned dipole into regions where magnitude the magnetic field is smaller.
Quantum Effects
As expected, the quantum picture is different. Pieter Zeeman was one of the first to observe the splittings of spectral lines in a magnetic field caused by this interaction. Consequently, such splittings are known as the Zeeman effect. Let’s now use our current knowledge to predict what the Zeeman effect for the 2p to 1s transition in hydrogen would look like, and then compare this prediction with a more complete theory. To understand the Zeeman effect, which uses a magnetic field to remove the degeneracy of different angular momentum states, we need to examine how an electron in a hydrogen atom interacts with an external magnetic field, \(\vec{B}\). Since magnetism results from the circular motion of charged particles, we should look for a relationship between the angular momentum \(\vec{L}\) and the magnetic dipole moment \(\vec{\mu} _m\).
The relationship between the magnetic dipole moment \(\vec{\mu} _m\) (also referred to simply as the magnetic moment) and the angular momentum \(\vec{L}\) of a particle with mass m and charge \(q\) is given by
\[ \vec{\mu} _m = \dfrac {q}{2m} \vec{L} \label {8.4.2}\]
For an electron, this equation becomes
\[ \vec{\mu} _m = - \dfrac {e}{2m_e} \vec{L} \label {8.4.3}\]
where the specific charge and mass of the electron have been substituted for \(q\) and \(m\). The magnetic moment for the electron is a vector pointing in the direction opposite to \(\vec{L}\), both of which classically are perpendicular to the plane of the rotational motion.
Exercise \(\PageIndex{1}\)
Will an electron in the ground state of hydrogen have a magnetic moment? Why or why not?
The relationship between the angular momentum of a particle and its magnetic moment is commonly expressed as a ratio, called the gyromagnetic ratio, \(\gamma\). Gyro is Greek for turn so gyromagnetic simply relates turning (angular momentum) to magnetism. Now you also know why the Greek sandwiches made with meat cut from a spit turning over a fire are called gyros.
\[ \gamma = \dfrac {\mu _m}{L} = \dfrac {q}{2m} \label {8.4.4}\]
In the specific case of an electron,
\[ \gamma _e = - \dfrac {e}{2m_e} \label {8.4.5}\]
Exercise \(\PageIndex{2}\)
Calculate the magnitude of the gyromagnetic ratio for an electron.
To determine the energy of a hydrogen atom in a magnetic field we need to include the operator form of the hydrogen atom Hamiltonian. The Hamiltonian always consists of all the energy terms that are relevant to the problem at hand.
\[ \hat {H} = \hat {H} ^0 + \hat {H} _m \label {8.4.6}\]
where \(\hat {H} ^0\) is the Hamiltonian operator in the absence of the field and \(\hat {H} _m\) is written using the operator forms of Equations \(\ref{8.4.1}\) and \(\ref{8.4.3}\)),
\[ \hat {H}_m = - \hat {\mu} \cdot \vec{B} = \dfrac {e}{2m_e} \hat {L} \cdot B \label {8.4.7}\]
The scalar product
\[ \hat {L} \cdot \vec{B} = \hat {L}_x B_x + \hat {L}_y B_y + \hat {L}_z B_z \label {8.4.8}\]
simplifies if the z-axis is defined as the direction of the external field because then \(B_x\) and \(B_y\) are automatically 0, and Equation \ref{8.4.6} becomes
\[ \hat {H} = \hat {H}^0 + \dfrac {eB_z}{2m_e} \hat {L} _z \label {8.4.9}\]
where \(B_z\) is the magnitude of the magnetic field, which is along the z-axis.
We now can ask, “What is the effect of a magnetic field on the energy of the hydrogen atom orbitals?” To answer this question, we will not solve the Schrödinger equation again; we simply calculate the expectation value of the energy, \(\left \langle E \right \rangle \), using the existing hydrogen atom wavefunctions and the new Hamiltonian operator.
\[ \left \langle E \right \rangle = \left \langle \hat {H}^0 \right \rangle + \dfrac {eB_z}{2m_e} \left \langle \hat {L} _z \right \rangle \label {8.4.10}\]
where
\[\left \langle \hat {H}^0 \right \rangle = \int \psi ^*_{n,l,m_l} \hat {H}^0 \psi _{n,l,m_l} d \tau = E_n \label {8.4.11}\]
and
\[\left \langle \hat {L}_z \right \rangle = \int \psi ^*_{n,l,m_l} \hat {L}_z \psi _{n,l,m_l} d \tau = m_l \hbar \label {8.4.12}\]
Exercise \(\PageIndex{3}\)
Show that the expectation value \(\left \langle \hat {L}_z \right \rangle = m_l \hbar\).
The expectation value approach provides an exact result in this case because the hydrogen atom wavefunctions are eigenfunctions of both \(\hat {H} ^0\) and \(\hat {L}_z\). If the wavefunctions were not eigenfunctions of the operator associated with the magnetic field, then this approach would provide a first-order estimate of the energy. First and higher order estimates of the energy are part of a general approach to developing approximate solutions to the Schrödinger equation. This approach, called perturbation theory, is discussed in the next chapter.
The expectation value calculated for the total energy in this case is the sum of the energy in the absence of the field, \(E_n\), plus the Zeeman energy, \(\dfrac {e \hbar B_z m_l}{2m_e}\)
\[\begin{align} \left \langle E \right \rangle &= E_n + \dfrac {e \hbar B_z m_l}{2m_e} \\[4pt] &= E_n + \mu _B B_z m_l \label {8.4.13} \end{align}\]
The factor
\[ \dfrac {e \hbar}{2m_e} = - \gamma _e \hbar = \mu _B \label {8.4.14}\]
defines the constant \(\mu _B\), called the Bohr magneton, which is taken to be the fundamental magnetic moment. It has units of \(9.2732 \times 10^{-21}\) erg/Gauss or \(9.2732 \times 10^{-24}\) Joule/Tesla. This factor will help you to relate magnetic fields, measured in Gauss or Tesla, to energies, measured in ergs or Joules, for any particle with a charge and mass the same as an electron.
Equation \ref{8.4.13} shows that the \(m_l\) quantum number degeneracy of the hydrogen atom is removed by the magnetic field. For example, the three states \(\psi _{211}\), \(\psi _{21-1}\), and \(\psi _{210}\), which are degenerate in zero field, have different energies in a magnetic field, as shown in Figure \(\PageIndex{3}\).
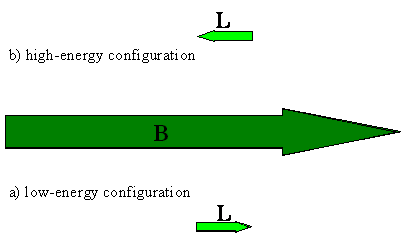
The \(m_l = 0\) state, for which the component of angular momentum and hence also the magnetic moment in the external field direction is zero, experiences no interaction with the magnetic field. The \(m_l = +1\) state, for which the angular momentum in the z-direction is +ħ and the magnetic moment is in the opposite direction, against the field, experiences a raising of energy in the presence of a field. Maintaining the magnetic dipole against the external field direction is like holding a small bar magnet with its poles aligned exactly opposite to the poles of a large magnet (Figure \(\PageIndex{5}\)). It is a higher energy situation than when the magnetic moments are aligned with each other.
Exercise \(\PageIndex{4}\)
Carry out the steps going from Equation \(\ref{8.4.10}\) to Equation \(\ref{8.4.13}\).
Exercise \(\PageIndex{5}\)
Consider the effect of changing the magnetic field on the magnitude of the Zeeman splitting. Sketch a diagram where the magnetic field strength is on the x-axis and the energy of the three 2p orbitals is on the y-axis to show the trend in splitting magnitudes with increasing magnetic field. Be quantitative, calculate and plot the exact numerical values using a software package of your choice.
Exercise \(\PageIndex{6}\)
Based on your calculations in Exercise \(\PageIndex{2}\) sketch a luminescence spectrum for the hydrogen atom in the n = 2 level in a magnetic field of 1 Tesla. Provide the numerical value for each of the transition energies. Use cm-1 or electron volts for the energy units.


