2.4: The Compton Effect

Last updated
Save as PDF

Page ID: 4477

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

The Compton effect concerns the inelastic scattering of x‑rays by electrons. Scattering means dispersing in different directions, and inelastic means that energy is lost by the scattered object in the process. The intensity of the scattered x‑ray is measured as a function of the wavelength shift \(\Delta \lambda\), where

\[ \lambda ' = \lambda + \Delta \lambda \label {2-6}\]

and the scattering angle \(\theta\).

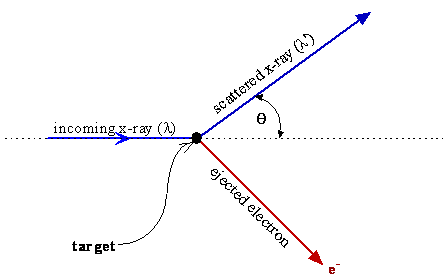
Figure \(\PageIndex{1}\): The Compton Effect. X-rays scattered from a target at an angle have a different wavelength from the incident x-ray, and produce an ejected electron.

To explain the experimental observations, it is necessary to describe the situation just as one would when discussing two particles, e.g. marbles, colliding and scattering from each other. The x‑ray scatters (changes direction) and causes an electron with mass me to be ejected from the object with a direction that conserves the momentum of the system. Momentum and energy conservation equations then explain the scattering angles and the observed wavelength shift of the x-ray when the momentum of the x-rays is taken to be equal to \(h/\lambda\) and the energy is \(h\nu\).

These considerations lead to Equation \(\ref{2-7}\), which describes the experimental data for the variation of \(\Delta \lambda\) with \(\theta\). The success of using energy and momentum conservation for two colliding particles to explain the experimental data for the Compton effect is powerful evidence that electromagnetic radiation has momentum just like a particle and that the momentum and energy are given by \(h/\lambda\) and \(h\nu\), respectively.

\[ \Delta \lambda = \frac {h}{m_ec} (1 - \cos \theta ) \label {2-7}\]

Example \(\PageIndex{1}\)

For Compton scattering, determine the wavelength shift at a scattering angle of \(90^o\), and identify the scattering angles where the wavelength shift is the smallest and the largest.