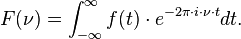32.10: Fourier Analysis

Last updated
Save as PDF

Page ID: 2338

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

The Fourier transform converts a function vs. continuous (or descrete) time and maps it into a function vs. continuous (or descrete) frequencies. Hence, the transform converts time-domain data into frequency-domain data (and vice versa). This decomposion of a function into sinusoids of different frequencies is a powerful approach to many experimental and theoretical problems. Fourier transform spectroscopy is an approach whereby spectra are collected based on measurements using time-domain or space-domain measurements of the electromagnetic radiation or other type of radiation. It can be applied to a variety of types of spectroscopy including optical spectroscopy, infrared spectroscopy (FT IR, FT-NIRS), Fourier transform nuclear magnetic resonance (NMR), mass spectrometry and electron spin resonance spectroscopy.

Introduction

Fourier analysis is a subject area which grew out of the study of Fourier series. The subject began with trying to understand when it was possible to represent general functions by sums of simpler trigonometric functions. The attempt to understand functions (or other objects) by breaking them into basic pieces that are easier to understand is one of the central themes in Fourier analysis. Fourier analysis is named after Joseph Fourier who showed that representing a function by a trigonometric series greatly simplified the study of heat propagation. Today the subject of Fourier analysis encompasses a vast spectrum of mathematics with parts that, at first glance, may appear quite different. In the sciences and engineering the process of decomposing a function into simpler pieces is often called an analysis. In Fourier analysis, the term Fourier transform often refers to the process that decomposes a given function into the basic pieces. This process results in another function that describes how much of each basic piece are in the original function. However, the transform is often given a more specific name depending upon the domain and other properties of the function being transformed, as elaborated below. Moreover, the original concept of Fourier analysis has been extended over time to apply to more and more abstract and general situations, and the general field is often known as harmonic analysis.

Fourier Series

When the function ƒ is a function of time and represents a physical signal, the transform has a standard interpretation as the frequency spectrum of the signal. The magnitude of the resulting complex-valued function F at frequency ω represents the amplitude of a frequency component whose initial phase is given by the phase of F. However, it is important to realize that Fourier transforms are not limited to functions of time, and temporal frequencies. They can equally be applied to analyze spatial frequencies, and indeed for nearly any function domain.

Properties

http://www.math.ubc.ca/~feldman/demos/demo3.html

Continuous Fourier Trasnform (CFT)

Most often, the unqualified term Fourier transform refers to the transform of functions of a continuous real argument, such as time (t). In this case the Fourier transform describes a function ƒ(t) in terms of basic complex exponentials of various frequencies. In terms of ordinary frequency ν, the Fourier transform is given by the complex number:

$F(\nu) = \int_{-\infty}^{\infty} f(t) \cdot e^{- 2\pi \cdot i \cdot \nu \cdot t} dt.$

Evaluating this quantity for all values of ν produces the frequency-domain function.

Discrete Fourier Transform (DFT)

Experimentally, we collect data that is not continuous, but samples a measurements at specific point. Hence we have to deal with the discrete version of the Fourier Transform.

Fast Fourier Transfer (FFT)

The discrete version of the Fourier transform (see below) can be evaluated quickly on computers using fast Fourier transform (FFT) algorithms. This algortihm sympically requires a 2ⁿ number of measurements to operate. Hence you will notice data sets often with such dimensions. (Conte & de Boor 1980)

References

Arfken, G. "Fourier Series." Ch. 14 in Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 760-793, 1985.
Askey, R. and Haimo, D. T. "Similarities between Fourier and Power Series." Amer. Math. Monthly 103, 297-304, 1996.
Beyer, W. H. (Ed.). CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, 1987.
Brown, J. W. and Churchill, R. V. Fourier Series and Boundary Value Problems, 5th ed. New York: McGraw-Hill, 1993.
Byerly, W. E. An Elementary Treatise on Fourier's Series, and Spherical, Cylindrical, and Ellipsoidal Harmonics, with Applications to Problems in Mathematical Physics. New York: Dover, 1959.
Carslaw, H. S. Introduction to the Theory of Fourier's Series and Integrals, 3rd ed., rev. and enl. New York: Dover, 1950.
Davis, H. F. Fourier Series and Orthogonal Functions. New York: Dover, 1963.
Dym, H. and McKean, H. P. Fourier Series and Integrals. New York: Academic Press, 1972.
Folland, G. B. Fourier Analysis and Its Applications. Pacific Grove, CA: Brooks/Cole, 1992.
Groemer, H. Geometric Applications of Fourier Series and Spherical Harmonics. New York: Cambridge University Press, 1996.
Körner, T. W. Fourier Analysis. Cambridge, England: Cambridge University Press, 1988.
Körner, T. W. Exercises for Fourier Analysis. New York: Cambridge University Press, 1993.
Krantz, S. G. "Fourier Series." §15.1 in Handbook of Complex Variables. Boston, MA: Birkhäuser, pp. 195-202, 1999.
Lighthill, M. J. Introduction to Fourier Analysis and Generalised Functions. Cambridge, England: Cambridge University Press, 1958.
Morrison, N. Introduction to Fourier Analysis. New York: Wiley, 1994.
Sansone, G. "Expansions in Fourier Series." Ch. 2 in Orthogonal Functions, rev. English ed. New York: Dover, pp. 39-168, 1991.
Weisstein, E. W. "Books about Fourier Transforms." http://www.ericweisstein.com/encyclopedias/books/FourierTransforms.html.
Whittaker, E. T. and Robinson, G. "Practical Fourier Analysis." Ch. 10 in The Calculus of Observations: A Treatise on Numerical Mathematics, 4th ed. New York: Dover, pp. 260-284, 1967.
R. R. Williams Spectroscopy and the Fourier Transform Wiley: New York, 1995
Bettis, Cliff; Lyons, Edward J.; Brooks, David W. J. Chem. Educ. 1996, 73, 839
Graff, Daria K. J. Chem. Educ. 1995, 72, 304.
Chesick, John P. J. Chem. Educ. 1989, 66, 128.
Glasser, L. J. Chem. Educ. 1987, 64, A228.
Glasser, L. J.Chem. Educ. 1987, 64, A255.
Glasser, L. J. Chem. Educ. 1987, 64, A306.

Contributors and Attributions

Wikipedia entry (to begin with)
mmrc.caltech.edu/FTIR/FTIRintro.pdf