28.4: Different Rate Laws Predict Different Kinetics
- Page ID
- 14546
Difference rate laws predict different kinetics
Zero-order Kinetics
Second Order Kinetics
Dinitrogen pentoxide (N2O5) decomposes to NO2 and O2 at relatively low temperatures in the following reaction:
\( 2N_{2}O_{5}\left ( soln \right ) \rightarrow 4NO_{2}\left ( soln \right )+O_{2}\left ( g \right ) \)
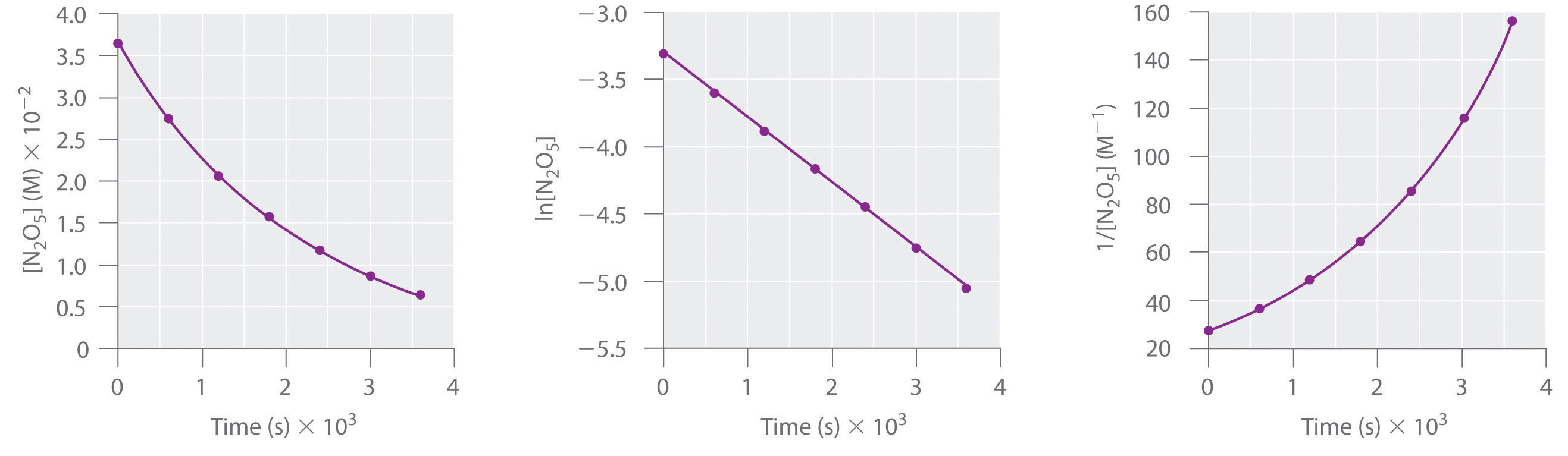
This reaction is carried out in a CCl4 solution at 45°C. The concentrations of N2O5 as a function of time are listed in the following table, together with the natural logarithms and reciprocal N2O5 concentrations. Plot a graph of the concentration versus t, ln concentration versus t, and 1/concentration versus t and then determine the rate law and calculate the rate constant.
| Time (s) | [N2O5] (M) | ln[N2O5] | 1/[N2O5] (M−1) |
|---|---|---|---|
| 0 | 0.0365 | −3.310 | 27.4 |
| 600 | 0.0274 | −3.597 | 36.5 |
| 1200 | 0.0206 | −3.882 | 48.5 |
| 1800 | 0.0157 | −4.154 | 63.7 |
| 2400 | 0.0117 | −4.448 | 85.5 |
| 3000 | 0.00860 | −4.756 | 116 |
| 3600 | 0.00640 | −5.051 | 156 |
Given: balanced chemical equation, reaction times, and concentrations
Asked for: graph of data, rate law, and rate constant
Strategy:
A Use the data in the table to separately plot concentration, the natural logarithm of the concentration, and the reciprocal of the concentration (the vertical axis) versus time (the horizontal axis). Compare the graphs with those in Figure 13.4.2 to determine the reaction order.
B Write the rate law for the reaction. Using the appropriate data from the table and the linear graph corresponding to the rate law for the reaction, calculate the slope of the plotted line to obtain the rate constant for the reaction.
Solution:
A Here are plots of [N2O5] versus t, ln[N2O5] versus t, and 1/[N2O5] versus t:
The plot of ln[N2O5] versus t gives a straight line, whereas the plots of [N2O5] versus t and 1/[N2O5] versus t do not. This means that the decomposition of N2O5 is first order in [N2O5].
B The rate law for the reaction is therefore
\( rate = k \left [N_{2}O_{5} \right ]\)
Calculating the rate constant is straightforward because we know that the slope of the plot of ln[A] versus t for a first-order reaction is −k. We can calculate the slope using any two points that lie on the line in the plot of ln[N2O5] versus t. Using the points for t = 0 and 3000 s,
\( slope= \dfrac{ln\left [N_{2}O_{5} \right ]_{3000}-ln\left [N_{2}O_{5} \right ]_{0}}{3000\;s-0\;s} = \dfrac{\left [-4.756 \right ]-\left [-3.310 \right ]}{3000\;s} =4.820\times 10^{-4}\;s^{-1} \)
Thus k = 4.820 × 10−4 s−1.
Contributors
- Anonymous
Modified by Joshua Halpern (Howard University), Scott Sinex, and Scott Johnson (PGCC)