27.1: The Average Translational Kinetic Energy of a Gas
- Page ID
- 14535
The laws that describe the behavior of gases were well established long before anyone had developed a coherent model of the properties of gases. In this section, we introduce a theory that describes why gases behave the way they do. The theory we introduce can also be used to derive laws such as the ideal gas law from fundamental principles and the properties of individual particles.
One key property of the individual particles is their velocity. However, in a sample of many gas particles, the particles will likely have various velocities. Rather than list the velocity of each individual gas molecule, we can combine these individual velocities in several ways to obtain "collective" velocities that describe the sample as a whole.
| Property | Speed | Kinetic Energy |
|---|---|---|
| Most probable | \( \sqrt{\dfrac{2k_bT}{m}}\) | \(k_BT\) |
| Average | \( \sqrt{\dfrac{8k_bT}{\pi m}}\) | \(\dfrac{4k_BT}{\pi}\) |
| Root-mean-square | \( \sqrt{\dfrac{3k_bT}{m}}\) | \( \dfrac{3}{2} k_BT\) |
In the following example, these three collective velocities are defined and calculated for a sample of gas consisting of only eight molecules.
The speeds of eight molecules were found to be 1.0, 4.0, 4.0, 6.0, 6.0, 6.0, 8.0, and 10.0 m/s. Calculate their average speed (\(v_{\rm avg}\)) root mean square speed (\(v_{\rm rms}\)), and most probable speed (\(v_{\rm mp}\)).
Solution
Start with definitions:
- average speed (\(v_{\rm avg}\)) = the sum of all the speeds divided by the number of molecules
- root-mean square speed (\(v_{\rm rms}\)) = the square root of the sum of the squared speeds divided by the number of molecules
- most probable speed (\(v_{\rm mp}\)) = the speed at which the greatest number of molecules is moving
The average speed:
\[\begin{align*} v_{\rm avg} &=\rm\dfrac{(1.0+4.0+4.0+6.0+6.0+6.0+8.0+10.0)\;m/s}{8} \\[4pt] &=5.6\;m/s \end{align*} \nonumber \]
The root-mean square speed:
\[\begin{align*}v_{\rm rms} &=\rm\sqrt{\dfrac{(1.0^2+4.0^2+4.0^2+6.0^2+6.0^2+6.0^2+8.0^2+10.0^2)\;m^2/s^2}{8}} \\[4pt] &=6.2\;m/s\end{align*} \nonumber \]
The most probable speed:
Of the eight molecules, three have speeds of 6.0 m/s, two have speeds of 4.0 m/s, and the other three molecules have different speeds. Hence
\[v_{\rm mp}=6.0\, m/s. \nonumber \]
Using expressions for \(v_{mp}\), \(v_{ave}\), or \(v_{rms}\), it is fairly simple to derive expressions for kinetic energy from the expression
\[E_{kin} = \dfrac{1}{2} mv^2 \nonumber \]
It is important to remember that there will be a full distribution of molecular speeds in a thermalized sample of gas. Some molecules will be traveling faster and some more slowly. It is also important to recognize that the most probable, average, and RMS kinetic energy terms that can be derived from the kinetic molecular theory do not depend on the mass of the molecules (Table 27.1.1). As such, it can be concluded that the average kinetic energy of the molecules in a thermalized sample of gas depends only on the temperature. However, the average speed depends on the molecular mass. So, for a given temperature, light molecules will travel faster on average than heavier molecules.
The calculations carried out in Example 27.1.1 become cumbersome as the number of molecules in the sample of gas increases. Thus, a more efficient way to determine the various collective velocities for a gas sample containing a large number of molecules is required.
A Molecular Description of Pressure and Molecular Speed
The kinetic molecular theory of gases explains the laws that describe the behavior of gases. Developed during the mid-19th century by several physicists, including the Austrian Ludwig Boltzmann (1844–1906), the German Rudolf Clausius (1822–1888), and the Scotsman James Clerk Maxwell (1831–1879), this theory is based on the properties of individual particles as defined for an ideal gas and the fundamental concepts of physics. Thus the kinetic molecular theory of gases provides a molecular explanation for observations that led to the development of the ideal gas law. The kinetic molecular theory of gases is based on the following five postulates:
- A gas is composed of a large number of particles called molecules (whether monatomic or polyatomic) that are in constant random motion.
- Because the distance between gas molecules is much greater than the size of the molecules, the volume of the molecules is negligible.
- Intermolecular interactions, whether repulsive or attractive, are so weak that they are also negligible.
- Gas molecules collide with one another and with the walls of the container, but these collisions are perfectly elastic; that is, they do not change the average kinetic energy of the molecules.
- The average kinetic energy of the molecules of any gas depends on only the temperature, and at a given temperature, all gaseous molecules have exactly the same average kinetic energy.

Figure 27.1.1 : Visualizing molecular motion. Molecules of a gas are in constant motion and collide with one another and with the container wall.
Although the molecules of real gases have nonzero volumes and exert both attractive and repulsive forces on one another, for the moment we will focus on how the kinetic molecular theory of gases relates to the properties of gases we have been discussing. In Topic 1C, we explain how this theory must be modified to account for the behavior of real gases.
Postulates 1 and 4 state that gas molecules are in constant motion and collide frequently with the walls of their containers. The collision of molecules with their container walls results in a momentum transfer (impulse) from molecules to the walls (Figure 27.1.2 ).
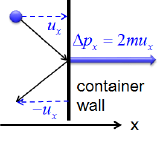
Figure 27.1.2 : Note: In this figure, the symbol \(u\) is used to represent velocity. In the rest of this text, velocity will be represented with the symbol \(v\). Momentum transfer (Impulse) from a molecule to the container wall as it bounces off the wall. Momentum transfer (\(\Delta \rho_x\)) for an elastic collision is equal to m\(\Delta v_x\), where m is the mass of the molecule and \(\Delta v_x\) is the change in the \(x\) component of the molecular velocity (\(v_{x_{final}}-v_{x_{initial}})\).The wall is perpendicular to \(x\) axis. Since the collisions are elastic, the molecule bounces back with the same velocity in the opposite direction, and \(\Delta v_x\) equals \(2v_x\).
The momentum transfer to the wall perpendicular to \(x\) axis as a molecule with an initial velocity \(v_x\) in the \(x\) direction hits is expressed as:
\[\rm momentum\; transfer_x\;= \Delta \rho_x = m\Delta v_x = 2mv_x \label{1.2.1} \]
The collision frequency, a number of collisions of the molecules to the wall per unit area and per second, increases with the molecular speed and the number of molecules per unit volume.
\[f\propto (v_x) \times \Big(\dfrac{N}{V}\Big) \label{1.2.2} \]
The pressure the gas exerts on the wall is expressed as the product of impulse and the collision frequency.
\[P\propto (2mv_x)\times(v_x)\times\Big(\dfrac{N}{V}\Big)\propto \Big(\dfrac{N}{V}\Big)mv_x^2 \label{1.2.3} \]
At any instant, however, the molecules in a gas sample are traveling at different speed. Therefore, we must replace \(v_x^2\) in the expression above with the average value of \(v_x^2\), which is denoted by \(\bar{v_x^2}\). The overbar designates the average value over all molecules.
The exact expression for pressure is given as :
\[P=\dfrac{N}{V}m\bar{v_x^2} \label{1.2.4} \]
Finally, we must consider that there is nothing special about \(x\) direction. We should expect that \(\bar{v_x^2}= \bar{v_y^2}=\bar{v_z^2}=\dfrac{1}{3}\bar{v^2}\). Here the quantity \(\bar{v^2}\) is called the mean-square speed defined as the average value of square-speed (\(v^2\)) over all molecules. Since \(v^2=v_x^2+v_y^2+v_z^2\) for each molecule, \(\bar{v^2}=\bar{v_x^2}+\bar{v_y^2}+\bar{v_z^2}\). By substituting \(\dfrac{1}{3}\bar{v^2}\) for \(\bar{v_x^2}\) in the expression above, we can get the final expression for the pressure:
\[P=\dfrac{1}{3}\dfrac{N}{V}m\bar{v^2} \label{1.2.5} \]
Because volumes and intermolecular interactions are negligible, postulates 2 and 3 state that all gaseous particles behave identically, regardless of the chemical nature of their component molecules. This is the essence of the ideal gas law, which treats all gases as collections of particles that are identical in all respects except mass. Postulate 2 also explains why it is relatively easy to compress a gas; you simply decrease the distance between the gas molecules.
Postulate 5 provides a molecular explanation for the temperature of a gas. Postulate 5 refers to the average translational kinetic energy of the molecules of a gas,
\[\epsilon = m\bar{v^2}/2\label{1.2.6} \]
By rearranging equation \(\ref{1.2.5}\) and substituting in equation \(\ref{1.2.6}\), we obtain
\[PV = \dfrac{1}{3} N m \bar{v^2} = \dfrac{2}{3} N \epsilon \label{1.2.7} \]
The 2/3 factor in the proportionality reflects the fact that velocity components in each of the three directions contributes ½ kT to the kinetic energy of the particle. The average translational kinetic energy is directly proportional to temperature:
\[\epsilon = \dfrac{3}{2} kT \label{1.2.8} \]
in which the proportionality constant \(k\) is known as the Boltzmann constant. Substituting Equation \(\ref{1.2.8}\) into Equation \(\ref{1.2.7}\) yields
\[ PV = \left( \dfrac{2}{3}N \right) \left( \dfrac{3}{2}kT \right) =NkT \label{1.2.9} \]
The Boltzmann constant \(k\) is just the gas constant per molecule, so if N is chosen as Avogadro's number, \(N_A\), then \(N_Ak\) is R, the gas constant per mole. Thus, for n moles of particles, the Equation \(\ref{1.2.9}\) becomes
\[ PV = nRT \label{1.2.10} \]
which is the ideal gas law.
As noted in Example 27.1.1 , the root-mean square speed (\(v_{\rm rms}\)) is the square root of the sum of the squared speeds divided by the number of particles:
\[v_{\rm rms}=\sqrt{\bar{v^2}}=\sqrt{\dfrac{v_1^2+v_2^2+\cdots v_N^2}{N}} \label{1.2.11} \]
where \(N\) is the number of particles and \(v_i\) is the speed of particle \(i\).
The \(v_{\rm rms}\) for a sample containing a large number of molecules can be obtained by combining equations \(\ref{1.2.7}\) and \(\ref{1.2.8}\) in a slightly different fashion than that used to obtain equation \(\ref{1.2.10}\):
\[PV=\dfrac{1}{3} N m \bar{v^2} = \dfrac{2}{3} N \epsilon \tag{27.1.10} \]
\[\epsilon = \dfrac{3}{2} kT \tag{27.1.11} \]
\[\dfrac{1}{3} N m \bar{v^2}= \left(\dfrac{2}{3}\right)\left(\dfrac{3}{2}\right) NkT \label{1.2.12} \]
\[\dfrac{1}{3} N m \bar{v^2}= NkT \label{1.2.13} \]
\[ N m \bar{v^2}= 3NkT \label{1.2.14} \]
If N is chosen to be Avogadro's number, \(N_A\), then \(N_Am = M\), the molar mass, and \(N_Ak = R\), the gas constant per mole,
\[\bar{v^2} = \dfrac{3RT}{M} \label{1.2.15} \]
\[v_{\rm rms}=\sqrt{\bar{v^2}}=\sqrt{\dfrac{3RT}{M}} \label{1.2.16} \]
In Equation \(\ref{1.2.16}\), \(v_{\rm rms}\) has units of meters per second; consequently, the units of molar mass \(M\) are kilograms per mole, temperature \(T\) is expressed in kelvins, and the ideal gas constant \(R\) has the value 8.3145 J/(K•mol). Equation \(\ref{1.2.16}\) shows that \(v_{\rm rms}\) of a gas is proportional to the square root of its Kelvin temperature and inversely proportional to the square root of its molar mass. The root mean-square speed of a gas increase with increasing temperature. At a given temperature, heavier gas molecules have slower speeds than do lighter ones.
What is the root mean-square speed for \(\rm O_2\) molecules at 25ºC?
Given: Temperature in ºC, type of molecules, ideal gas gas constant
Asked for: \(v_{\rm rms}\), the root mean-square speed
Strategy:
Convert temperature to kelvins:
\(\rm T\; (in\; kelvin) = (25ºC + 273ºC)\dfrac{1\; K}{1\; ºC} = 298\; K\)
Convert molar mass of \(\rm O_2\) molecules to kg per mole:
\(\rm M\; (in\; \dfrac{kg}{mole}) = 32.00\dfrac{g}{mole}\rm x\dfrac{1\; kg}{1000\; g}=0.03200\dfrac{kg}{mole}\)
Use equation \(\ref{1.2.16}\) to calculate the rms speed.
Solution
\(v_{\rm rms_{\rm O_2}}= \sqrt{\dfrac{3\rm (8.3145\dfrac{J}{K·mole})(298.15\; K)}{\rm 0.03200\dfrac{kg}{mole}}}=482\dfrac{m}{s}\)
What is the root mean-square speed for \(\rm Cl_2\) molecules at 25ºC?
\(v_{\rm rms_{\rm Cl_2}}= 324\dfrac{m}{s}\)
Many molecules, many velocities
At temperatures above absolute zero, all molecules are in motion. In the case of a gas, this motion consists of straight-line jumps whose lengths are quite great compared to the dimensions of the molecule. Although we can never predict the velocity of a particular individual molecule, the fact that we are usually dealing with a huge number of them allows us to know what fraction of the molecules have kinetic energies (and hence velocities) that lie within any given range.
The trajectory of an individual gas molecule consists of a series of straight-line paths interrupted by collisions. What happens when two molecules collide depends on their relative kinetic energies; in general, a faster or heavier molecule will impart some of its kinetic energy to a slower or lighter one. Two molecules having identical masses and moving in opposite directions at the same speed will momentarily remain motionless after their collision.
If we could measure the instantaneous velocities of all the molecules in a sample of a gas at some fixed temperature, we would obtain a wide range of values. A few would be zero, and a few would be very high velocities, but the majority would fall into a more or less well-defined range. We might be tempted to define an average velocity for a collection of molecules, but here we would need to be careful: molecules moving in opposite directions have velocities of opposite signs. Because the molecules are in a gas are in random thermal motion, there will be just about as many molecules moving in one direction as in the opposite direction, so the velocity vectors of opposite signs would all cancel and the average velocity would come out to zero. Since this answer is not very useful, we need to do our averaging in a slightly different way.
The proper treatment is to average the squares of the velocities, and then take the square root of this value to obtain the root-mean-square velocity (\(v_{\rm rms}\)), which is what we developed above. This velocity describes the gas sample as a whole, but it does not tell us about the range of velocities possible, nor does it tell us the distribution of velocities. To obtain a more complete description of how many gas molecules are likely to be traveling at a given velocity range we need to make use of the Maxwell-Boltzmann distribution law.
Contributors and Attributions
- Tom Neils, Grand Rapids Community College (editing)

