26.7: The van 't Hoff Equation
- Page ID
- 14528
We can use Gibbs-Helmholtz to get the temperature dependence of \(K\)
\[ \left( \dfrac{∂[ΔG^o/T]}{∂T} \right)_P = \dfrac{-ΔH^o}{T^2} \nonumber \]
At equilibrium, we can equate \(ΔG^o\) to \(-RT\ln K\) so we get:
\[ \left( \dfrac{∂[\ln K]}{∂T} \right)_P = \dfrac{ΔH^o}{RT^2} \nonumber \]
We see that whether \(K\) increases or decreases with temperature is linked to whether the reaction enthalpy is positive or negative. If temperature is changed little enough that \(ΔH^o\) can be considered constant, we can translate a \(K\) value at one temperature into another by integrating the above expression, we get a similar derivation as with melting point depression:
\[\ln \dfrac{K(T_2)}{K(T_1)} = \dfrac{-ΔH^o}{R} \left( \dfrac{1}{T_2} - \dfrac{1}{T_1} \right) \nonumber \]
If more precision is required we could correct for the temperature changes of \(ΔH^o\) by using heat capacity data.
How \(K\) increases or decreases with temperature is linked to whether the reaction enthalpy is positive or negative.
The expression for \(K\) is a rather sensitive function of temperature given its exponential dependence on the difference of stoichiometric coefficients One way to see the sensitive temperature dependence of equilibrium constants is to recall that
\[K=e^{−\Delta_r{G^o}/RT}\label{18} \]
However, since under constant pressure and temperature
\[\Delta{G^o}= \Delta{H^o}−T\Delta{S^o} \nonumber \]
Equation \(\ref{18}\) becomes
\[ K=e^{-\Delta{H^o}/RT} e^{\Delta {S^o}/R}\label{19} \]
Taking the natural log of both sides, we obtain a linear relation between \(\ln K \)and the standard enthalpies and entropies:
\[\ln K = - \dfrac{\Delta {H^o}}{R} \dfrac{1}{T} + \dfrac{\Delta{S^o}}{R}\label{20} \]
which is known as the van ’t Hoff equation. It shows that a plot of \(\ln K\) vs. \(1/T\) should be a line with slope \(-\Delta_r{H^o}/R\) and intercept \(\Delta_r{S^o}/R\).
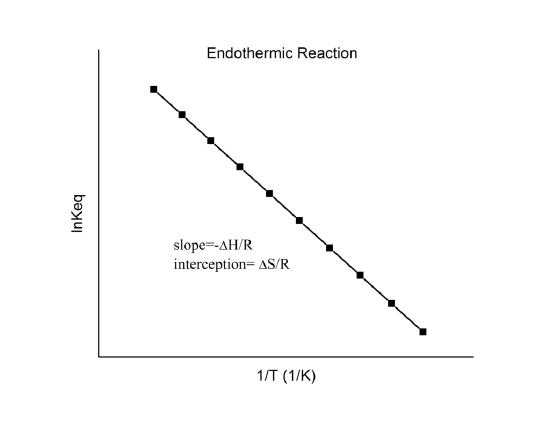
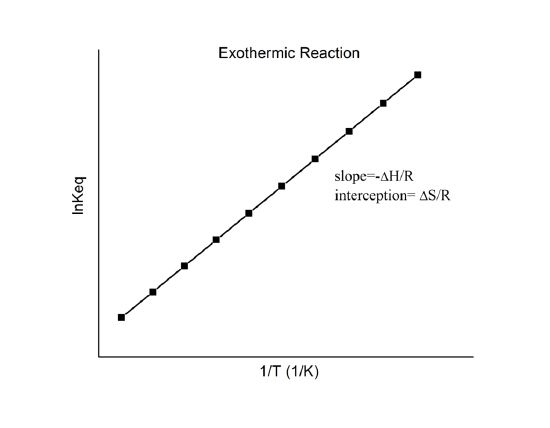
Hence, these quantities can be determined from the \(\ln K\) vs. \(1/T\) data without doing calorimetry. Of course, the main assumption here is that \(\Delta_r{H^o}\) and \(\Delta_r{S^o}\) are only very weakly dependent on \(T\), which is usually valid.


