25.4: Osmotic Pressure can Determine Molecular Masses
- Page ID
- 14516
Some membrane materials are permeable for some molecules, but not for others. This is often a matter of the size of the molecules, but it can also be a question of solubility of the molecule in the barrier material. Many biological membranes have semipermeable properties and osmosis is therefore an important biological process. Figure 25.4.1 shows a simple osmotic cell. Both compartments contain water, but the one on the right also contains a solute whose molecules (represented by green circles) are too large to pass through the membrane. Many artificial and natural substances are capable of acting as semi-permeable membranes. For example, the walls of most plant and animal cells fall into this category.
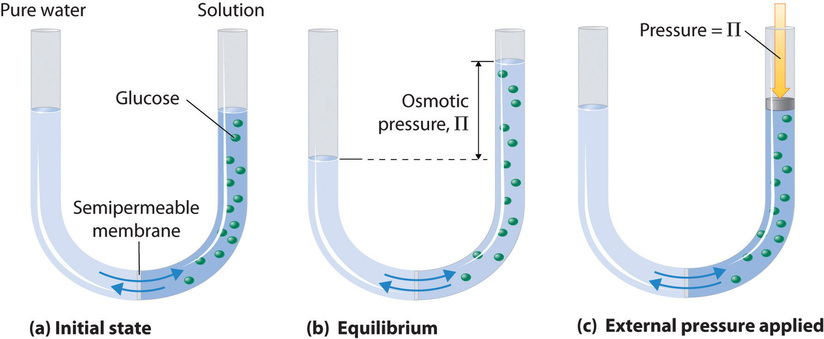
If solvent molecules can pass through the membrane, but solute molecules (or ions) cannot, solvent molecules will spontaneously migrate across the membrane to increase the solution's volume and thus reduce its concentration. If the solution is ideal, this process is in many ways analogous to the spontaneous increase in volume of a gas allowed to expand against vacuum. Of course the volume of the 'solute-gas' is limited by the availability of solvent and, if done under gravity in a U-shaped tube, by the build up of hydrostatic pressure. This pressure is known as the osmotic pressure \(\Pi\). At equilibrium we can write:
\[μ^*(T,P) = μ^{sln}(T,P+ Π,a_1) \nonumber \]
\[μ^*(T,P) = μ^*(T,P+ Π)+ RT\ln a_1 \nonumber \]
From Gibbs energy (\(dG\)) in its natural variables (\(P,T\)) we know that:
\[ \left(\dfrac{∂G}{∂P} \right)_{T,x} = V \nonumber \]
Taking the partial versus \(x_1\) we get:
\[ \left( \dfrac{∂μ^*}{∂P} \right)_{T,x_{j}} = \bar{V}^*_{1} \nonumber \]
This means we can integrate over the molar volume to convert \(μ^*(T,P+ Π)\) to a different pressure:
\[μ^*(T,P+\Pi) = μ^*(T,P) + \int_P^{P+ \Pi} \bar{V}^*_{1} dP \nonumber \]
Thus we get:
\[μ^*(T,P) = μ^*(T,P+ \Pi)+ RT\ln a_1 \nonumber \]
\[μ^*(T,P) = μ^*(T,P)+ \Pi\bar{V}^*_{1}+ RT\ln a_1 \nonumber \]
Once again using the ideal approximation:
\[\ln a_1 \ln x_1 ≈ -x_2 \nonumber \]
we get:
\[RT x_2 = \Pi\bar{V}^*_{1} \nonumber \]
\[x_2 = \dfrac{n_2}{n_1+n_2}≈\dfrac{n_2}{n_1} \nonumber \]
The combination gives an expression involving the molarity:
\[\Pi=RTc \nonumber \]
Where \(c\) is the molar concentration. Osmosis can be used in reverse, if we apply about 30 bar to sea water we can obtain fresh water on the other side of a suitable membrane. This process is used in some places, but better membranes would be desirable and they easily get clogged. The resulting water is not completely salt-free and this means that if used for agriculture the salt may accumulate on the field over time.
Determining Molar Masses
Both melting point depression and boiling point elevation only facilitate the determination of relatively small molar weights. The need for such measurements is no longer felt because we now have good techniques to determine the structure of most small to medium size molecules. For polymers this is a different matter. They usually have a molecular weight (mass) distribution and determining it is an important topic of polymer science.
Osmometry is still of some practical usefulness. It is also colligative and able to measure up to about 8000 daltons. Many polymers are much bigger than that. Their mass distribution is usually determined by different means. The polymers is dissolved and led over a chromatographic column usually based on size-exclusion. The effluent is then probed as function of the elution time by a combination of techniques:
- UV absorption (determine the monomer concentration)
- Low Angle Laser Light Scattering (LALLS) and/or Viscometry
The latter two provide information on the molar mass distribution but they give a different moment of that distribution. The combination of techniques gives an idea not only of how much material there is of a given molar mass but also of the linearity or degree of branching of the chains.
Nevertheless melting point depression is still used in a somewhat different application. When a slightly impure solid is melted its melting point in depressed. Also the melting process is not sudden but takes place over the whole trajectory from typically a lower eutectic temperature up to the depressed melting point (the liquid line in the phase diagram). In organic synthesis the melting behavior is often used as a first convenient indication of purity. In a differential scanning calorimetry (DSC) experiment the melting peak becomes progressively skewed towards lower temperatures at higher impurity levels. The shape of the curve can be modeled with a modified version of the melting point depression expression. This yields a value for the total impurity level in the solid. This technique is used in the pharmaceutical industry for quality control purposes.

