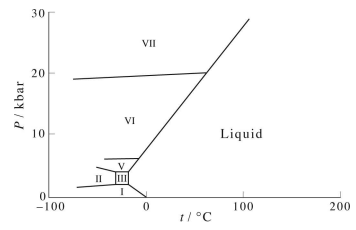
23.2: Gibbs Energies and Phase Diagrams
- Page ID
- 14498
First Order Transitions
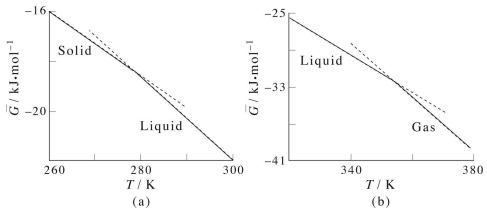
The following plot shows the Gibbs energy as a function of temperature, including phase changes from solid to liquid (melting) and liquid to gas (boiling).
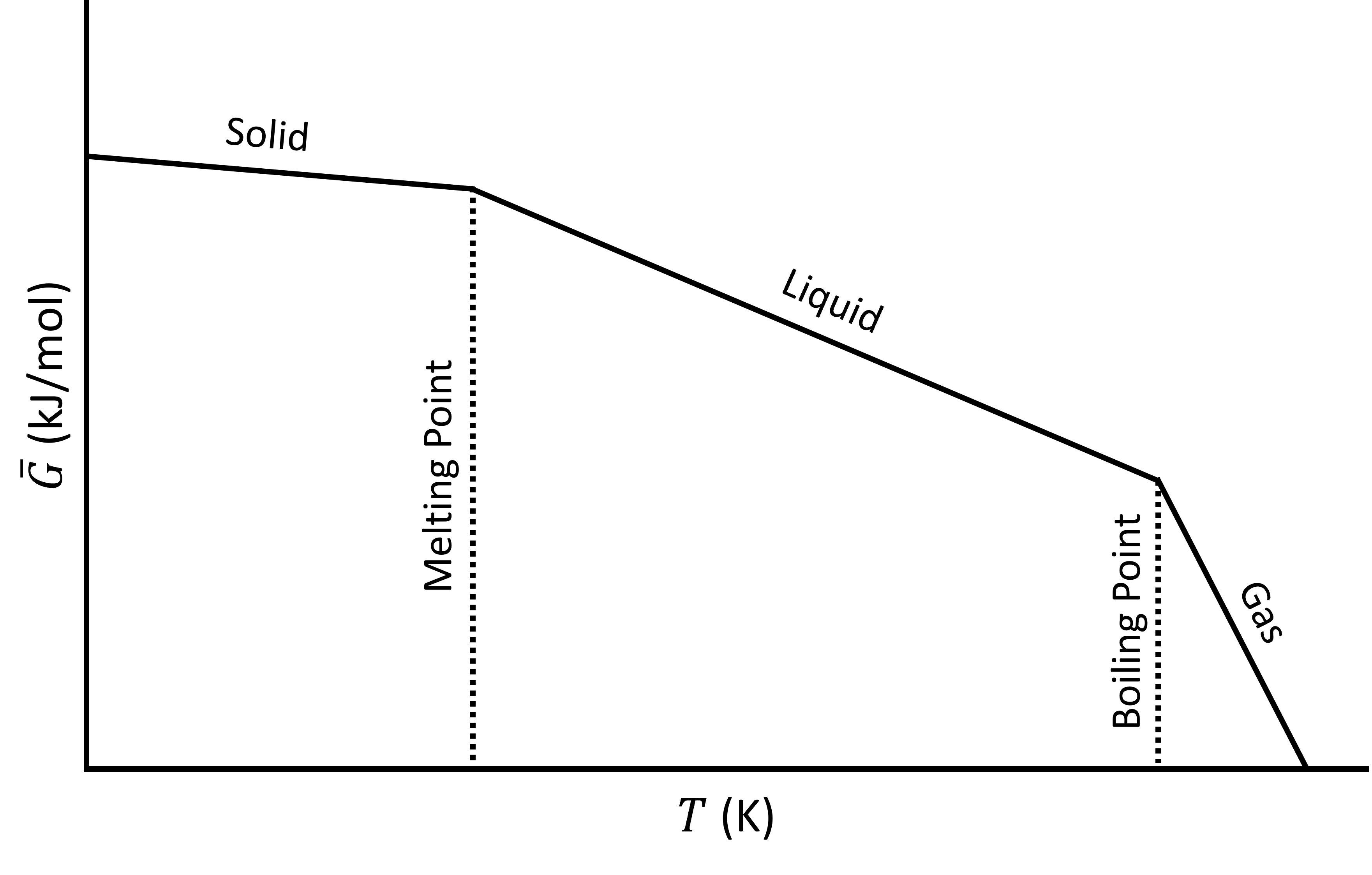
Gibbs energy (\(\bar{G}\)) as a function of temperature (\(T\)).
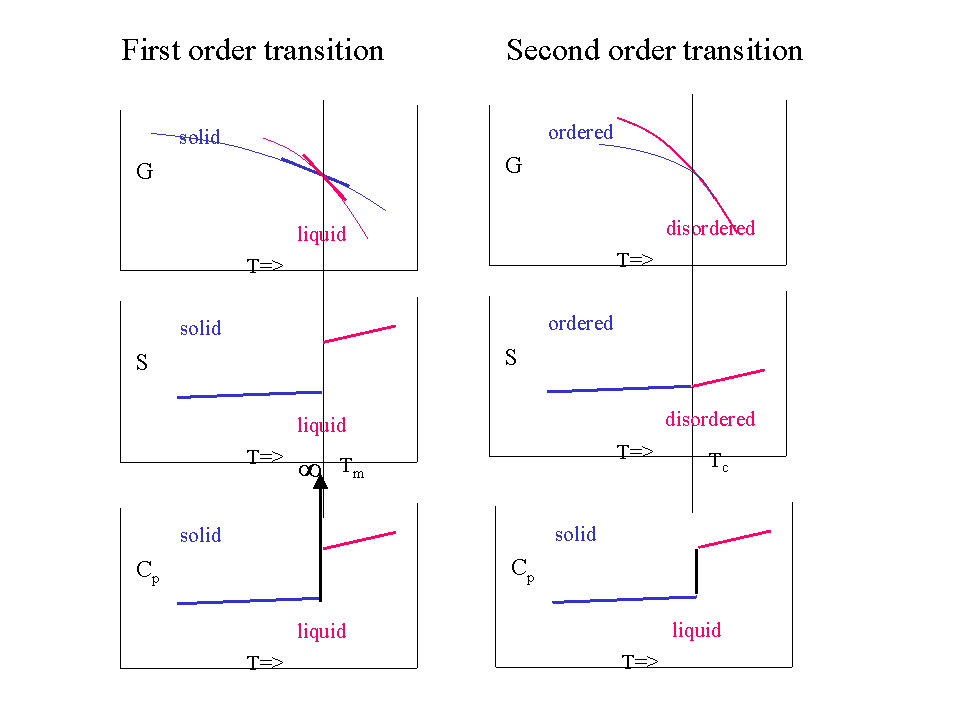
Although the \(G\) curve is continuous, its first order derivatives (\(-S\)) is discontinuous at the phase changes. This is why this transition it called a first order transition. We could say that:
- \(G\) is continuous but has a kink
- The first order derivatives (\(H\),\(S\),..) are discontinuous (have a jump)
- The second order derivatives (\(C_P\), ..) have a singularity (go to ∞)
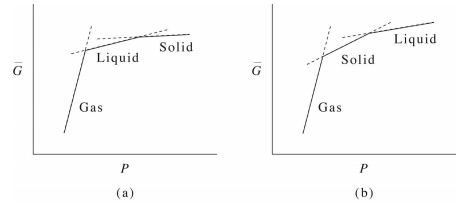
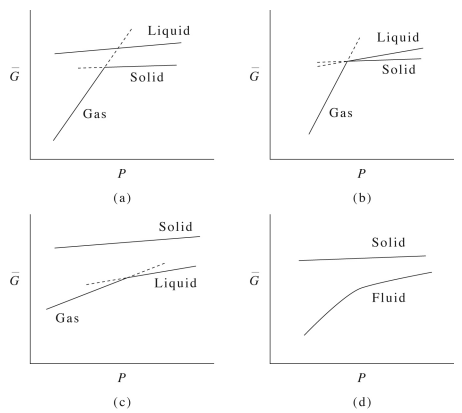
Second Order Transitions
More subtle transitions where \(G\) is continuous, \(H\) and \(S\) are also continuous but have a kink and the discontinuity is only found in the second order derivatives (such as \(C_P\)) also exist. They are called second order transitions. In such a case:
- \(G\) is continuous and has no kink
- The first order derivatives (\(H\),\(S\),..) are continuous (but have a kink)
- The second order derivatives (\(C_P\), ..) are discontinuous (have a jump)
| Transition Order | Function | 1st Order | 2nd Order |
|---|---|---|---|
| 0 | G,A | kink | smooth |
| 1 | H,S,V,.. | jump | kink |
| 2 | CP,CV,α,κ | sing. ∞ | jump |
This classification goes back to Ehrenfest. Obviously it based on the question: what order derivative is the first to go discontinuous? Of course we could extend this principle and define third order transitions but there are reasons to be doubtful that such things exist. Another problem is that it is assumed that the order must be integer: 1,2, etc. Is it possible to have a transition of intermediate non-integer order, say 1.3? Although derivatives of fractional order are beyond the scope of the chemistry curriculum the mathematics does exist (Liouville).
Conjugate Variables
As discussed before there are many other forms of work possible, such as electrical work, magnetic work or elastic work. These they are commonly incorporated in the formalism of thermodynamics by adding other terms, e.g:
\[dG = -SdT + VdP + ℰde + MdH + FdL + γdA \nonumber \]
- ℰde stands for the electromotoric force ℰ and de the amount of charge transported against it.
- MdH stand for magnetization and (change in) magnetic field.
- F stands for the elastic force of e.g. a rubber band dL for the length it is stretched
- γ stands for the surface tension (e.g. of a soap bubble), A for its surafce area.
The terms always appear in a pair of what is known as conjugate variables. That is even clearer if we write out the state function rather than its differential form:
\[G = U + PV -TS + ℰe + MH + FL + γA + ... \nonumber \]
The PV term can also be generalized -and needs to be so- for a viscous fluid to a stress-strain conjugate pair. It then involves a stress tensor. We will soon encounter another conjugate pair: μdn that deals with changes in composition (n) and the thermodynamic potential μ.