12.4: Symmetry Operations as Matrices
- Page ID
- 13487
Matrices can be used to map one set of coordinates or functions onto another set. Matrices used for this purpose are called transformation matrices. The symmetry operations in a group may be represented by a set of transformation matrices \(\Gamma\)\((g)\), one for each symmetry element \(g\). Each individual matrix is called a representative of the corresponding symmetry operation, and the complete set of matrices is called a matrix representation of the group. The matrix representatives act on some chosen basis set of functions, and the actual matrices making up a given representation will depend on the basis that has been chosen. The representation is then said to span the chosen basis. The basis we will use are unit vectors pointing in the \(x\), \(y\), and \(z\) directions.
The transformation matrix for any operation in a group has a form that is unique from the matrices of the other members of the same group; however, the character of the transformation matrix for a given operation is the same as that for any other operation in the same class. Each symmetry operation below will operate on an arbitrary vector, \(\bf{u}\):
\[ \bf{u} = \begin{pmatrix} x \\ y \\ z \end{pmatrix}\]
The Identity Operation, \(E\)
The first rule is that the group must include the identity operation \(E\) (the ‘do nothing’ operation). The matrix representative of the identity operation is simply the identity matrix and leaves the vector unchanged:
\[ E\bf{u} = \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} x \\ y \\ z \end{pmatrix} = \begin{pmatrix} x \\ y \\ z \end{pmatrix} \label{9.1} \]
Every matrix representation includes the appropriate identity matrix.
The Reflection Operation, \(\sigma\)
The reflection operation reflects the vector \(\bf{u}\) over a plane. This can be the \(xy\), \(xz\), or \(yz\) plane. The matrix is similar to the identity matrix, with the exception that there is a sign change for the appropriate element. The reflect matrix in the \(xy\) plane is:
\[ \sigma (xy) \bf{u} = \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & -1 \end{pmatrix} \begin{pmatrix} x \\ y \\ z \end{pmatrix} = \begin{pmatrix} x \\ y \\ -z \end{pmatrix} \label{9.2} \]
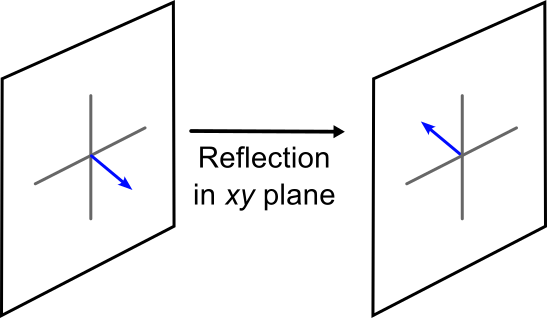
Notice that the element for the dimension being reflected is the on that is negative. In the above case, since \(z\) is being reflected over the \(xy\) plane, the \(z\) element in the matrix is negative. If we were to reflect over the \(xz\) plane instead, the \(y\) element would be the one that is negative:
\[ \sigma (xz) \bf{u} = \begin{pmatrix} 1 & 0 & 0 \\ 0 & -1 & 0 \\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} x \\ y \\ z \end{pmatrix} = \begin{pmatrix} x \\ -y \\ z \end{pmatrix} \]
The \(n\)-fold Rotation Operation, \(C_n\)
The \(C_n\) operator rotates the molecule about an axis. The counterclockwise rotation of vector \(\bf{u}\) about the \(z\) axis is:
\[ C_n\bf{u} = \begin{pmatrix} \cos{\frac{2\pi}{n}} & -\sin{\frac{2\pi}{n}} & 0 \\ \sin{\frac{2\pi}{n}} & \cos{\frac{2\pi}{n}} & 0 \\ 0 & 0 & 1 \end{pmatrix}
\begin{pmatrix} x \\ y \\ z \end{pmatrix} =
\begin{pmatrix} x' \\ y' \\ z \end{pmatrix} \]
For clockwise rotation, the sign on the \(\sin{\theta}\) terms are reversed. This matrix simplifies dramatically for the \(C_2\) rotation:
\[ C_2\bf{u} = \begin{pmatrix} -1 & 0 & 0 \\ 0 & -1 & 0 \\ 0 & 0 & 1 \end{pmatrix}
\begin{pmatrix} x \\ y \\ z \end{pmatrix} =
\begin{pmatrix} -x \\ -y \\ z \end{pmatrix} \]
Rotation matrices operating about the \(x\), \(y\) and \(z\) axes are given by:
\[R_{x}(\theta) = \begin{pmatrix} 1 & 0 & 0 \\ 0 & \cos\theta & -\sin\theta \\ 0 & \sin\theta & \cos\theta \end{pmatrix} \label{9.6a} \]
\[R_{y}(\theta) = \begin{pmatrix} \cos\theta & 0 & -\sin\theta \\ 0 & 1 & 0 \\ \sin\theta & 0 & \cos\theta \end{pmatrix} \label{9.6b} \]
\[R_{z}(\theta) = \begin{pmatrix} \cos\theta & -\sin\theta & 0 \\ \sin\theta & \cos\theta & 0 \\ 0 & 0 & 1 \end{pmatrix} \label{9.6c} \]
The Inversion operation, \(I\)
The inversion operation inverts every point:
\[ I\bf{u} = \begin{pmatrix} -1 & 0 & 0 \\ 0 & -1 & 0 \\ 0 & 0 & -1 \end{pmatrix}
\begin{pmatrix} x \\ y \\ z \end{pmatrix} =
\begin{pmatrix} -x \\ -y \\ -z \end{pmatrix} \]
\(C_{2v}\) Point Group
Now that we have seen the matrix form of our operators, we can see how the multiplication of each operator leads to another operations in the group. The \(C_{2v}\) multiplication table is:
| \(C_{2v}\) | \(E\) | \(C_2\) | \(\sigma_v\) | \(\sigma_v'\) |
|---|---|---|---|---|
| \(E\) | \(E\) | \(C_2\) | \(\sigma_v\) | \(\sigma_v'\) |
| \(C_2\) | \(C_2\) | \(E\) | \(\sigma_v'\) | \(\sigma_v\) |
| \(\sigma_v\) | \(\sigma_v\) | \(\sigma_v'\) | \(E\) | \(C_2\) |
| \(\sigma_v'\) | \(\sigma_v'\) | \(\sigma_v\) | \(C_2\) | \(E\) |
For multiplication tables, the standard order of operation is the row elements (top) first, following by the column element (side). Every row or column includes every operation once and is different from any other row or column.
Let's look at \(C_2 \sigma_v\) multiplication, where \(\sigma_v\) is a reflection across the \(xz\) plane:
\[ C_2 \sigma_v = \begin{pmatrix} -1 & 0 & 0 \\ 0 & -1 & 0 \\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} 1 & 0 & 0 \\ 0 & -1 & 0 \\ 0 & 0 & 1 \end{pmatrix}
= \begin{pmatrix} -1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix} = \sigma_v' \]
where \(\sigma_v'\) is the reflection across the \(yz\) plane.
Matrix Representations and Groups
Before proceeding any further, we must check that a matrix representation of a group obeys all of the rules set out in the formal mathematical definition of a group.
- Identity.The first rule is that the group must include the identity operation \(E\) (the ‘do nothing’ operation). We showed above that the matrix representative of the identity operation is simply the identity matrix. As a consequence, every matrix representation includes the appropriate identity matrix.
- Closure. The second rule is that the combination of any pair of elements must also be an element of the group (the group property). If we multiply together any two matrix representatives, we should get a new matrix which is a representative of another symmetry operation of the group. In fact, matrix representatives multiply together to give new representatives in exactly the same way as symmetry operations combine according to the group multiplication table. For example, in the \(C_{2v}\) point group, we showed that the combined symmetry operation \(C_2\)\(\sigma_v\) is equivalent to \(\sigma_v'\). In a matrix representation of the group, if the matrix representatives of \(C_2\) and \(\sigma_v\) are multiplied together, the result will be the representative of \(\sigma_v'\).
- Associativity. The third rule states that the rule of combination of symmetry elements in a group must be associative. This is automatically satisfied by the rules of matrix multiplication.
- Reciprocality. The final rule states that every operation must have an inverse, which is also a member of the group. The combined effect of carrying out an operation and its inverse is the same as the identity operation. It is fairly easy to show that matrix representatives satisfy this criterion. For example, the inverse of a reflection is another reflection, identical to the first. In matrix terms we would therefore expect that a reflection matrix was its own inverse, and that two identical reflection matrices multiplied together would give the identity matrix. This turns out to be true, and can be verified using any of the reflection matrices in the examples above. The inverse of a rotation matrix is another rotation matrix corresponding to a rotation of the opposite sense to the first.
We often use sets of atomic orbitals as basis functions for matrix representations. In this example, we’ll take as our basis a \(p\) orbital on each carbon atom \(\begin{pmatrix} p_1, p_2, p_3 \end{pmatrix}\).
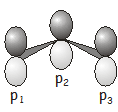
Note that the \(p\) orbitals are perpendicular to the plane of the carbon atoms (this may seem obvious, but if you’re visualizing the basis incorrectly it will shortly cause you a not inconsiderable amount of confusion). The symmetry operations in the \(C_{2v}\) point group, and their effect on the three \(p\) orbitals, are as follows:
\[\begin{array}{ll} E & \begin{pmatrix} p_1 \\ p_2 \\ p_3 \end{pmatrix} \rightarrow \begin{pmatrix} p_1 \\ p_2 \\ p_3 \end{pmatrix} \\
C_2 & \begin{pmatrix} p_1 \\ p_2 \\ p_3 \end{pmatrix} \rightarrow \begin{pmatrix} -p_3 \\ -p_2 \\ -p_1 \end{pmatrix} \\
\sigma_v & \begin{pmatrix} p_1 \\ p_2 \\ p_3 \end{pmatrix} \rightarrow \begin{pmatrix} -p_1 \\ -p_2 \\ -p_3 \end{pmatrix} \\
\sigma_v' & \begin{pmatrix} p_1 \\ p_2 \\ p_3 \end{pmatrix} \rightarrow \begin{pmatrix} p_1 \\ p_2 \\ p_3 \end{pmatrix} \end{array} \nonumber \]
The matrices that carry out the transformation are
\[\begin{array}{ll} \Gamma(E) & \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} p_1 \\ p_2 \\ p_3 \end{pmatrix} = \begin{pmatrix} p_1 \\ p_2 \\ p_3 \end{pmatrix} \\
\Gamma(C_2) & \begin{pmatrix} 0 & 0 & -1 \\ 0 & -1 & 0 \\ -1 & 0 & 0 \end{pmatrix} \begin{pmatrix} p_1 \\ p_2 \\ p_3 \end{pmatrix} = \begin{pmatrix} -p_3 \\ -p_2 \\ -p_1 \end{pmatrix} \\
\Gamma(\sigma_v) & \begin{pmatrix} -1 & 0 & 0 \\ 0 & -1 & 0 \\ 0 & 0 & -1 \end{pmatrix} \begin{pmatrix} p_1 \\ p_2 \\ p_3 \end{pmatrix} = \begin{pmatrix} -p_1 \\ -p_2 \\ -p_3 \end{pmatrix} \\
\Gamma(\sigma_v') & \begin{pmatrix} 0 & 0 & 1 \\ 0 & 1 & 0 \\ 1 & 0 & 0 \end{pmatrix} \begin{pmatrix} p_1 \\ p_2 \\ p_3 \end{pmatrix} = \begin{pmatrix} p_1 \\ p_2 \\ p_3 \end{pmatrix} \end{array} \nonumber \]

