5.8: The Energy Levels of a Rigid Rotor
- Page ID
- 13422
- Compare the classical and quantum rigid rotor in three dimensions
- Demonstrate how to use the Separation of Variable technique to solve the 3D rigid rotor Schrödinger Equation
- Identify and interpret the two quantum numbers for a 3D quantum rigid rotor including the range of allowed values
- Describe the wavefunctions of the 3D quantum rigid rotor in terms of nodes, average displacements and most probable displacements
- Describe the energies of the 3D quantum rigid rotor in terms of values and degeneracies
Rigid rotor means when the distance between particles do not change as they rotate. A rigid rotor only approximates a rotating diatomic molecular if vibration is ignored.
The Classical Rigid Rotor in 3D
The rigid rotor is a mechanical model that is used to explain rotating systems. The linear rigid rotor model consists of two point masses located at fixed distances from their center of mass. The fixed distance between the two masses and the values of the masses are the only characteristics of the rigid model. However, for many actual diatomics this model is too restrictive since distances are usually not completely fixed and corrections on the rigid model can be made to compensate for small variations in the distance. Even in such a case the rigid rotor model is a useful model system to master.
For a rigid rotor, the total energy is the sum of kinetic (\(T\)) and potential (\(V\)) energies
\[E_{tot} = T + V \label{5.8.2} \]
The potential energy, \(V\), is set to \(0\) because the distance between particles does not change within the rigid rotor approximation. However, In reality, \(V \neq 0\) because even though the average distance between particles does not change, the particles still vibrate. The rigid rotor approximation greatly simplifys our discussion.
Since \(V=0\) then \(E_{tot} = T\) and we can also say that:
\[T = \dfrac{1}{2}\sum{m_{i}v_{i}^2} \label{5.8.3} \]
However, we have to determine \(v_i\) in terms of rotation since we are dealing with rotation motion. Since,
\[\omega = \dfrac{v}{r} \label{5.8.4} \]
where \(\omega\) is the angular velocity, we can say that:
\[v_{i} = \omega{X}r_{i} \label{5.8.5} \]
Thus we can rewrite Equation \(\ref{5.8.3}\) as:
\[T = \dfrac{1}{2}\sum{m_{i}v_{i}\left(\omega{X}r_{i}\right)} \label{5.8.6} \]
Since \(\omega\) is a scalar constant, we can rewrite Equation \ref{5.8.6} as:
\[T = \dfrac{\omega}{2}\sum{m_{i}\left(v_{i}{X}r_{i}\right)} = \dfrac{\omega}{2}\sum{l_{i}} = \omega\dfrac{L}{2} \label{5.8.7} \]
where \(l_i\) is the angular momentum of the ith particle, and \(L\) is the angular momentum of the entire system. Also, we know from physics that,
\[L = I\omega \label{5.8.9} \]
where \(I\) is the moment of inertia of the rigid body relative to the axis of rotation. We can rewrite Equation \(\ref{5.8.3}\) as
\[T = \omega\dfrac{{I}\omega}{2} = \dfrac{1}{2}{I}\omega^2 \label{5.8.10} \]
Equation \ref{5.8.10} shows that the energy of the rigid rotor scales with increasing angular frequency (i.e., the faster is rotates) and with increasing moment of inertia (i.e, the inertial resistance to rotation). Also, as expected, the classical rotational energy is not quantized (i.e., all possible rotational frequencies are possible).
The Quantum Rigid Rotor in 3D
It is convenient to discuss rotation with in the spherical coordinate system rather than the Cartesian system (Figure 5.8.1 ).
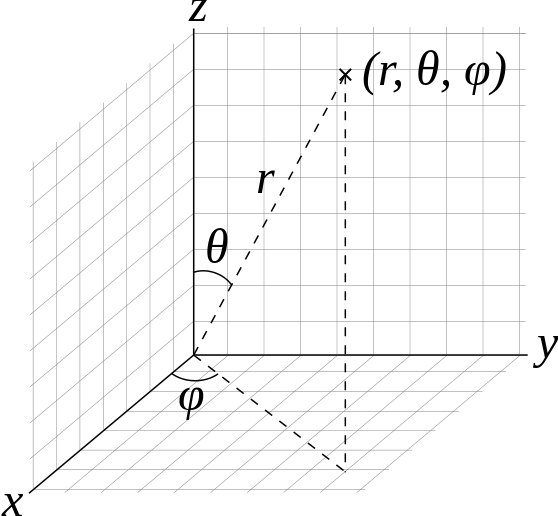
To solve the Schrödinger equation for the rigid rotor, we will separate the variables and form single-variable equations that can be solved independently. Only two variables \(\theta\) and \(\varphi\) are required in the rigid rotor model because the bond length, \(r\), is taken to be the constant \(r_0\). We first write the rigid rotor wavefunctions as the product of a theta-function depending only on \(\theta\) and a phi-function depending only on \(\varphi\)
\[ | \psi (\theta , \varphi ) \rangle = | \Theta (\theta ) \Phi (\varphi) \rangle \label {5.8.11} \]
We then substitute the product wavefunction and the Hamiltonian written in spherical coordinates into the Schrödinger Equation \(\ref{5.8.12}\)
\[\hat {H} | \Theta (\theta ) \Phi (\varphi) \rangle = E | \Theta (\theta ) \Phi (\varphi) \rangle \label {5.8.12} \]
to obtain
\[ -\dfrac {\hbar ^2}{2\mu r^2_0} \left [ \dfrac {\partial}{\partial r_0} r^2_0 \dfrac {\partial}{\partial r_0} + \dfrac {1}{\sin \theta} \dfrac {\partial}{\partial \theta } \sin \theta \dfrac {\partial}{\partial \theta } + \dfrac {1}{\sin ^2 \theta} \dfrac {\partial ^2}{\partial \varphi ^2} \right ] | \Theta (\theta ) \Phi (\varphi) \rangle = E | \Theta (\theta) \Phi (\varphi) \rangle \label {5.8.13} \]
Since \(r = r_0\) is constant for the rigid rotor and does not appear as a variable in the functions, the partial derivatives with respect to \(r\) are zero; i.e. the functions do not change with respect to \(r\). We also can substitute the symbol \(I\) for the moment of inertia, \(\mu r^2_0\) in the denominator of the left hand side of Equation \(\ref{5.8.13}\), to give
\[-\dfrac {\hbar ^2}{2I} \left [ \dfrac {1}{\sin \theta} \dfrac {\partial}{\partial \theta } \sin \theta \dfrac {\partial}{\partial \theta } + \dfrac {1}{\sin ^2 \theta} \dfrac {\partial ^2}{\partial \varphi ^2}\right ] | \Theta (\theta ) \Phi (\varphi) \rangle = E | \Theta (\theta) \Phi (\varphi) \rangle \label {5.8.14} \]
To begin the process of the Separating of Variables technique, multiply each side of Equation \(\ref{5.8.14}\) by \(\dfrac {2I}{\hbar ^2}\) and \(\dfrac {-\sin ^2 \theta}{\Theta (\theta) \Phi (\varphi)} \) to give
\[\dfrac {1}{\Theta (\theta) \psi (\varphi)} \left [ \sin \theta \dfrac {\partial}{\partial \theta } \sin \theta \dfrac {\partial}{\partial \theta } + \dfrac {\partial ^2}{\partial \varphi ^2}\right ] \Theta (\theta ) \Phi (\varphi) = \dfrac {-2IE \sin ^2 \theta}{\hbar ^2} \label {5.8.15} \]
Simplify the appearance of the right-hand side of Equation \(\ref{5.8.15}\) by defining a parameter \(\lambda\):
\[ \lambda = \dfrac {2IE}{\hbar ^2}. \label {5.8.16} \]
Note that this \(\lambda\) has no connection to a wavelength; it is merely being used as an algebraic symbol for the combination of constants shown in Equation \(\ref{5.8.16}\).
Inserting \(\lambda\), evaluating partial derivatives, and rearranging Equation \(\ref{5.8.15}\) produces
\[\dfrac {1}{\Theta (\theta)} \left [ \sin \theta \dfrac {\partial}{\partial \theta } \left (\sin \theta \dfrac {\partial}{\partial \theta } \right ) \Theta (\theta) + \left ( \lambda \sin ^2 \theta \right ) \Theta (\theta) \right ] = - \dfrac {1}{\Phi (\varphi)} \dfrac {\partial ^2}{\partial \varphi ^2} \Phi (\varphi) \label {5.8.17} \]
Carry out the steps leading from Equation \(\ref{5.8.15}\) to Equation \(\ref{5.8.17}\). Keep in mind that, if \(y\) is not a function of \(x\),
\[ \dfrac {dy}{dx} = y \dfrac {d}{dx} \nonumber \]
Equation \(\ref{5.8.17}\) says that the function on the left, depending only on the variable \(\theta\), always equals the function on the right, depending only on the variable \(\varphi\), for all values of \(\theta\) and \(\varphi\). The only way two different functions of independent variables can be equal for all values of the variables is if both functions are equal to a constant (review separation of variables). We call this constant \(m_J^2\) because soon we will need the square root of it. The two differential equations to solve are the \(\theta\)-equation
\[\sin \theta \dfrac {d}{d \theta} \left ( \sin \theta \dfrac {d}{d \theta} \right ) \Theta (\theta ) + \left ( \lambda \sin ^2 \theta - m_J^2 \right ) \Theta (\theta ) = 0 \label {5.8.18} \]
and the \(\varphi\)-equation
\[ \dfrac {d^2}{d \varphi ^2} \Phi (\varphi ) + m_J^2 \Phi (\varphi) = 0 \label {5.8.21} \]
The partial derivatives have been replaced by total derivatives because only a single variable is involved in each equation.
Often \(m_J\) is referred to as just \(m\) for convenience.
Show how Equations \(\ref{5.8.18}\) and \(\ref{5.8.21}\) are obtained from Equation \(\ref{5.8.17}\).
Solving the \(\varphi\) Equation
The \(\varphi\)-equation is similar to the Schrödinger Equation for the free particle. Since we already solved this previously, we immediately write the solutions:
\[ \Phi _m (\varphi) = N e^{\pm im_J \varphi} \label {5.8.22} \]
where we introduce the number \(m\) to track how many wavelengths of the wavefunction occur around one rotation (similar to the wavelength description of the Bohr atom).
Substitute Equation \(\ref{5.8.22}\) into Equation \(\ref{5.8.21}\) to show that it is a solution to that differential equation.
- Answer
-
Substitute
\[\Phi_m(\varphi)= \mathrm{N} e^{\pm \mathrm{i} m_{J} \varphi} \nonumber \]
into
\[\frac{d^{2}}{d \varphi^{2}} \Phi(\varphi)+m_{J}^{2} \Phi(\varphi)=0 \nonumber \]
\[\begin{aligned}
\frac{d^{2}}{d \varphi^{2}} \Phi_{\mathrm{m}}(\varphi)+m_{J}^{2} \Phi_{\mathrm{m}}(\varphi)=& \frac{d}{d \varphi}\left(\mathrm{N}\left(\pm \mathrm{i} m_{J}\right) e^{\pm \mathrm{i} m_{J} \varphi}\right)+m_{J}^{2} \Phi_{\mathrm{m}}(\varphi) \\
&\left.=\mathrm{N}\left(\pm \mathrm{i} m_{J}\right)^{2} e^{\pm i m_{J} \varphi}\right)+m_{J}^{2}\left(\mathrm{N} e^{\pm \mathrm{i} m_{J} \varphi}\right) \\
&=-\mathrm{N} m_{J}^{2} e^{\pm i m_{J} \varphi}+\mathrm{N} m_{J}^{2} e^{\pm i m_{J} \varphi}=0
\end{aligned} \nonumber \]Thus
\[\Phi_{m}(\varphi)=N e^{\pm i m_{J} \varphi} \nonumber \]
is a solution to the differential equations.
The normalization condition, Equation \(\ref{5.8.23}\) is used to find a value for \(N\) that satisfies Equation \(\ref{5.8.22}\).
\[ \int \limits ^{2 \pi} _0 \Phi ^*(\varphi) \Phi (\varphi) d \varphi = 1 \label {5.8.23} \]
The range of the integral is only from \(0\) to \(2π\) because the angle \(\varphi\) specifies the position of the internuclear axis relative to the x-axis of the coordinate system and angles greater than \(2π\) do not specify additional new positions.
Use the normalization condition in Equation \(\ref{5.8.23}\) to demonstrate that \(N = 1/\sqrt{2π}\).
- Answer
-
We need to evaluate Equation \ref{5.8.23} with \(\psi(\varphi)=N e^{\pm i m J \varphi} \)
\[\begin{align*} \psi^{*}(\varphi) \psi(\varphi) &= N e^{+i m J \varphi} N e^{-i m J \varphi} \\[4pt] &=N^{2} \\[4pt] 1=\int_{0}^{2 \pi} N^* N d \varphi=1 & \\[4pt] N^{2} (2 \pi) =1 \\[4pt] N=\sqrt{1 / 2 \pi} \end{align*} \nonumber \]
Values for \(m\) are found by using a cyclic boundary condition. The cyclic boundary condition means that since \(\varphi\) and \(\varphi + 2\varphi \) refer to the same point in three-dimensional space, \(\Phi (\varphi)\) must equal \(\Phi (\varphi + 2 \pi )\), i.e.
\[ \begin{align} e^{im_J \varphi} &= e^{im_J (\varphi + 2\pi)} \label{5.8.24} \\[4pt] &= e^{im_J\varphi} e^{im_J2\pi} \label {5.8.25} \end{align} \]
For the equality in Equation \(\ref{5.8.25}\) to hold, \(e^{i m_J 2 \pi}\) must equal 1, which is true only when
\[m_J = \cdots , -3, -2, -1, 0, 1, 2, 3, \cdots \label {5.8.26} \]
In other words \(m_J\) can equal any positive or negative integer or zero.
Use Euler’s Formula to show that \(e^{im_J2\pi}\) equals 1 for \(m_J\) equal to zero or any positive or negative integer.
Thus, the \(Φ\) function is
\[\Phi _{m_J} (\varphi) = \sqrt{\dfrac{1}{2\pi}} e^{\pm i m_J \varphi} \nonumber \]
with
\[ m_J = 0, \pm 1, \pm 2, \cdots \nonumber \]
Solving the \(\Theta (\theta)\) Equation
Finding the \(\Theta (\theta)\) functions that are solutions to the \(\theta\)-equation (Equation \(\ref{5.8.18}\)) is a more complicated process. Solutions are found to be a set of power series called Associated Legendre Functions (Table M2), which are power series of trigonometric functions, i.e., products and powers of sine and cosine functions. The \(\Theta (\theta)\) functions, along with their normalization constants, are shown in the third column of Table 5.8.1 .
|
|
|
|
|
|
|---|---|---|---|---|
| 0 | 0 | \(\dfrac {1}{\sqrt {2}}\) | \(\dfrac {1}{\sqrt {2 \pi}}\) | \(\dfrac {1}{\sqrt {4 \pi}}\) |
| 0 | 1 | \(\sqrt {\dfrac {3}{2}}\cos \theta\) | \(\dfrac {1}{\sqrt {2 \pi}}\) | \(\sqrt {\dfrac {3}{4 \pi}}\cos \theta\) |
| 1 | 1 | \(\sqrt {\dfrac {3}{4}}\sin \theta\) | \(\dfrac {1}{\sqrt {2 \pi}}e^{i \varphi}\) | \(\sqrt {\dfrac {3}{8 \pi}}\sin \theta e^{i \varphi}\) |
| -1 | 1 | \(\sqrt {\dfrac {3}{4}}\sin \theta\) | \(\dfrac {1}{\sqrt {2 \pi}}e^{-i\varphi}\) | \(\sqrt {\dfrac {3}{8 \pi}}\sin \theta e^{-i \varphi}\) |
| 0 | 2 | \(\sqrt {\dfrac {5}{8}}(3\cos ^2 \theta - 1)\) | \(\dfrac {1}{\sqrt {2 \pi}}\) | \(\sqrt {\dfrac {5}{16\pi}}(3\cos ^2 \theta - 1)\) |
| 1 | 2 | \(\sqrt {\dfrac {15}{4}} \sin \theta \cos \theta \) | \(\dfrac {1}{\sqrt {2 \pi}}e^{i \varphi}\) | \(\sqrt {\dfrac {15}{8\pi}} \sin \theta \cos \theta e^{i\varphi}\) |
| -1 | 2 | \(\sqrt {\dfrac {15}{4}} \sin \theta \cos \theta \) | \(\dfrac {1}{\sqrt {2 \pi}}e^{-i\varphi}\) | \(\sqrt {\dfrac {15}{8\pi}} \sin \theta \cos \theta e^{-i\varphi}\) |
| 2 | 2 | \(\sqrt {\dfrac {15}{16}} \sin ^2 \theta \) | \(\dfrac {1}{\sqrt {2 \pi}}e^{2i\varphi}\) | \(\sqrt {\dfrac {15}{32\pi}} \sin ^2 \theta e^{2i\varphi} \) |
| -2 | 2 | \(\sqrt {\dfrac {15}{16}} \sin ^2 \theta \) | \(\dfrac {1}{\sqrt {2 \pi}}e^{2i\varphi}\) | \(\sqrt {\dfrac {15}{32\pi}} \sin ^2 \theta e^{-2i\varphi} \) |
The solution to the \(\theta\)-equation requires that \(λ\) in Equation \(\ref{5.8.17}\) be given by
\[\lambda = J (J + 1) \label {5.8.28} \]
where
\[ J \ge |m_J| \label {5.8.29} \]
\(J\) can be 0 or any positive integer greater than or equal to \(m_J\). Each pair of values for the quantum numbers, \(J\) and \(m_J\), identifies a rotational state with a wavefunction (Equation \(\ref{5.8.11}\)) and energy (below). Equation \(\ref{5.8.29}\) means that \(J\) controls the allowed values of \(m_J\).
Each pair of values for the quantum numbers, \(J\) and \(m_J\), identifies a rotational state and hence a specific wavefunction with associated energy.
The combination of Equations \(\ref{5.8.16}\) and \(\ref{5.8.28}\) reveals that the energy of this system is quantized.
\[ E = \dfrac {\hbar ^2 \lambda}{2I} = J(J + 1) \dfrac {\hbar ^2}{2I} \label {5.8.30} \]
Using Equation \(\ref{5.8.30}\), you can construct a rotational energy level diagram (Figure 5.8.2 ). For simplicity, use energy units of \(\dfrac {\hbar ^2}{2I}\).
- \(J=0\): The lowest energy state has \(J = 0\) and \(m_J = 0\). This state has an energy \(E_0 = 0\). There is only one state with this energy, i.e. one set of quantum numbers, one wavefunction, and one set of properties for the molecule.
- \(J=1\): The next energy level is \(J = 1\) with energy \(\dfrac {2\hbar ^2}{2I}\). There are three states with this energy because \(m_J\) can equal +1, 0, or ‑1. These different states correspond to different orientations of the rotating molecule in space. States with the same energy are said to be degenerate. The degeneracy of an energy level is the number of states with that energy. The degeneracy of the \(J = 1\) energy level is 3 because there are three states with the energy \(\dfrac {2\hbar ^2}{2I}\).
- \(J=2\): The next energy level is for \(J = 2\). The energy is \(\dfrac {6\hbar ^2}{2I}\), and there are five states with this energy corresponding to \(m_J = +2, \,+1,\, 0,\, ‑1,\, ‑2\). The energy level degeneracy is five. Note that the spacing between energy levels increases as J increases. Also note that the degeneracy increases. The degeneracy is always \(2J+1\) because \(m_J\) ranges from \(+J\) to \(‑J\) in integer steps, including 0.
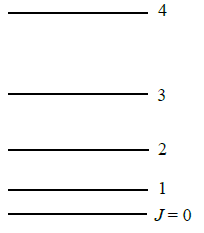
Each allowed energy of rigid rotor is \((2J+1)\)-fold degenerate. Hence, there exist \((2J+1)\) different wavefunctions with that energy.
Compute the energy levels for a rotating molecule for \(J = 0\) to \(J = 5\) using units of \(\dfrac {\hbar ^2}{2I}\).
- Answer
-
This rotating molecule can be assumed to be a rigid rotor molecule. From solving the Schrödinger equation for a rigid rotor we have the relationship for energies of each rotational eigenstate (Equation \ref{5.8.30}):
\[E = J(J+1)(ħ^2/2I) \nonumber \]
Using this equation, we can plug in the different values of the \(J\) quantum number so that
For J=0, \(E = (0)(1)(ħ^2/2I) = 0\) For J=1, \(E = (1)(2)(ħ^2/2I) = 2(ħ^2/2I)\) - This shows that as \(J\) increases, the energy levels get farther apart (Figure 5.8.2 ).
-
- For J=2, \(E = (2)(3)(ħ^2/2I) = 6(ħ^2/2I)\)
- For J=3, \(E = (3)(4)(ħ^2/2I) = 12(ħ^2/2I)\)
- For J=4, \(E = (4)(5)(ħ^2/2I) = 20(ħ^2/2I)\)
- For J=5, \(E = (5)(6)(ħ^2/2I) = 30(ħ^2/2I)\)
For \(J = 0\) to \(J = 5\), identify the degeneracy of each energy level and the values of the \(m_J\) quantum number that go with each value of the \(J\) quantum number. Construct a rotational energy level diagram including \(J = 0\) through \(J=5\). Label each level with the appropriate values for the quantum numbers \(J\) and \(m_J\). Describe how the spacing between levels varies with increasing \(J\).
- Answer
-
This rotating molecule can be assumed to be a rigid rotor molecule. From solving the Schrödinger equation for a rigid rotor, we have: \[λ = 2IE/ħ^2 \nonumber \]
Where λ is an arbitrary parameter not related to wavelength. Additionally, λ is assigned a quantum relation so that \[λ = J(J+1) \nonumber \]
Thus, combining the two equations and solving for E yields \[E = J(J+1)(ħ^2/2I) \nonumber \]
Using this equation, we can plug in the different values of J so that
- For J=0, \(E = (0)(1)(ħ^2/2I) = 0\)
- For J=1, \(E = (1)(2)(ħ^2/2I) = 2(ħ^2/2I)\)
- For J=2, \(E = (2)(3)(ħ^2/2I) = 6(ħ^2/2I)\)
- For J=3, \(E = (3)(4)(ħ^2/2I) = 12(ħ^2/2I)\)
- For J=4, \(E = (4)(5)(ħ^2/2I) = 20(ħ^2/2I)\)
- For J=5, \(E = (5)(6)(ħ^2/2I) = 30(ħ^2/2I)\)
This shows that as \(J\) increases, the energy levels get closer and closer together.
The \(m_J\) quantum number reflects the component of the angular momentum along the \(z\) direction (and hence is sometimes called the azimuthal quantum number). For a fixed value of \(J\), the different values of \(m_J\) reflect the different directions the angular momentum vector could be pointing – for large, positive \(m_J\) the angular momentum is mostly along +z; if \(m_J\) is zero the angular momentum is orthogonal to \(z\). Physically, the energy of the rotation does not depend on the direction, which is reflected in the fact that the energy depends only on \(J\) (Equation \(\ref{5.8.30}\)), which measures the length of the vector, not its direction given mb \(m_J\).
Calculate \(J = 0\) to \(J = 1\) rotational transition of the \(\ce{O2}\) molecule with a bond length of 121 pm.
Solution
\[E = \dfrac {\hbar^2}{I} = \dfrac {\hbar^2}{\mu r^2} \nonumber \]
\[\mu_{O2} = \dfrac{m_{O} m_{O}}{m_{O} + m_{O}} = \dfrac{(15.9994)(15.9994)}{15.9994 + 15.9994} = 7.9997 \nonumber \]
convert from atomic units to kilogram using the conversion: 1 au = 1.66 x 10-27 kg. Plug and chug.
\[E = 5.71 \times 10^{-27} \;Joules \nonumber \]
Spherical Harmonics
A wavefunction that is a solution to the rigid rotor Schrödinger Equation (Equation \(\ref{5.8.11}\)) can be written as a single function \(Y(\theta, \varphi)\), which is called a spherical harmonic function.
\[ Y^{m_J} _J (\theta , \varphi ) = \Theta ^{|m_J|}_J (\theta) \Phi _{m_J} (\varphi) \label {5.8.31} \]
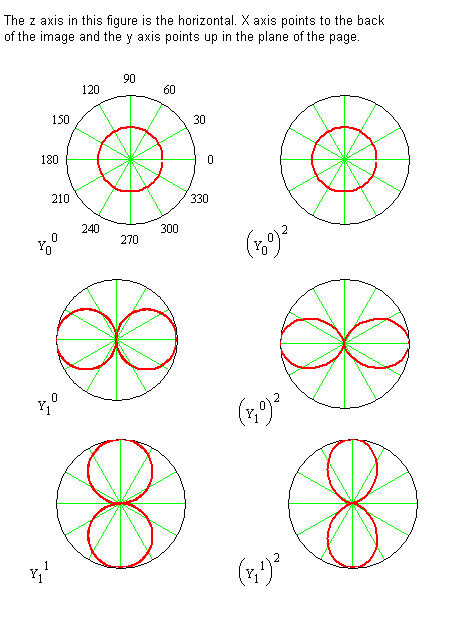
The spherical harmonic wavefunction is labeled with \(m_J\) and \(J\) because its functional form depends on both of these quantum numbers. These functions are tabulated above for \(J = 0\) through \(J = 2\) and for \(J = 3\) in the Spherical Harmonics Table (M4) Polar plots of some of the \(\theta\)-functions are shown in Figure 5.8.3 .
The two-dimensional space for a rigid rotor is defined as the surface of a sphere of radius \(r_0\), as shown in Figure 5.8.2 .
The probability of finding the internuclear axis at specific coordinates \(\theta _0\) and \(\varphi _0\) within an infinitesimal area \(ds\) on this curved surface is given by
\[ Pr \left [ \theta _0, \varphi _0 \right ] = Y^{m_{J*}}_J (\theta _0, \varphi _0) Y^{m_J}_J (\theta _0, \varphi _0) ds \label {5.8.32} \]
where the area element \(ds\) is centered at \(\theta _0\) and \(\varphi _0\).
Within the Copenhagen interpretation of wavefunctions, the absolute square (or modulus squared) of the rigid rotor wavefunction \(Y^{m_{J*}}_J (\theta, \varphi) Y^{m_J}_J (\theta, \varphi) \) gives the probability density for finding the internuclear axis oriented at \(\theta\) to the z-axis and \(\varphi\) to the x-axis. In spherical coordinates the area element used for integrating \(\theta\) and \(\varphi\) is
\[ds = \sin \theta\, d \theta \,d \varphi \label {5.8.33} \]
Use calculus to evaluate the probability of finding the internuclear axis of a molecule described by the \(J = 1\), \(m_J = 0\) wavefunction somewhere in the region defined by a range in \(\theta\) of 0° to 45°, and a range in of 0° to 90°. Note that a double integral will be needed. Sketch this region as a shaded area on Figure 5.8.1 .
Consider the significance of the probability density function by examining the \(J = 1\), \(m_J = 0\) wavefunction. The Spherical Harmonic for this case is
\[ Y^0_1 = \sqrt{ \dfrac {3}{4 \pi}} \cos \theta \label {5.8.34} \]
The polar plot of \(( Y^0_1)^2\) is shown in Figure 5.8.1 . For \(J = 1\) and \(m_J = 0\), the probability of finding the internuclear axis is independent of the angle \(\varphi\) from the x-axis, and greatest for finding the internuclear axis along the z‑axis, but there also is a probability for finding it at other values of \(\theta\) as well. So, although the internuclear axis is not always aligned with the z-axis, the probability is highest for this alignment. Also, since the probability is independent of the angle \(\varphi\), the internuclear axis can be found in any plane containing the z-axis with equal probability.
The \(J = 1\), \(m_J = 0\) function is 0 when \(\theta\) = 90°. Therefore, the entire xy-plane is a node. This fact means the probability of finding the internuclear axis in this particular horizontal plane is 0 in contradiction to our classical picture of a rotating molecule. In the classical picture, a molecule rotating in a plane perpendicular to the xy‑plane must have the internuclear axis lie in the xy‑plane twice every revolution, but the quantum mechanical description says that the probability of being in the xy-plane is zero. This conclusion means that molecules are not rotating in the classical sense, but they still have some, but not all, of the properties associated with classical rotation. The properties they retain are associated with angular momentum.
For each state with \(J = 0\) and \(J = 1\), use the function form of the \(Y\) spherical harmonics and Figure 5.8.1 to determine the most probable orientation of the internuclear axis in a diatomic molecule, i.e., the most probable values for \(\theta\) and \(\theta\).
Write a paragraph describing the information about a rotating molecule that is provided in the polar plot of \(Pr [\theta, \theta ] \) for the \(J = 1\), \(m_J = \pm 1\) state in Figure 5.8.1 . Compare this information to the classical picture of a rotating object.
Summary
There are two quantum numbers that describe the quantum behavior of a rigid rotor in three-deminesions: \(J\) is the total angular momentum quantum number and \(m_J\) is the z-component of the angular momentum. The spherical harmonics called \(Y_J^{m_J}\) are functions whose probability \(|Y_J^{m_J}|^2\) has the well known shapes of the s, p and d orbitals etc learned in general chemistry.
References
- Anderson, J.M. Introduction to Quantum Chemistry, 1969, W.A. Benjamin, Inc, pg.91-100.
- Atkins, Peter and de Paula, Julio. Physical Chemistry for the Life Sciences. New York: W.H. Freeman and Company. p. 515.
Contributors and Attributions
- Ian Huh
David M. Hanson, Erica Harvey, Robert Sweeney, Theresa Julia Zielinski ("Quantum States of Atoms and Molecules")
- MIT OpenCourseWare (Robert Guy Griffin and Troy Van Voorhis)

