1.1: Blackbody Radiation Cannot Be Explained Classically
- Page ID
- 13381
One experimental phenomenon that could not be adequately explained by classical physics was blackbody radiation. Objectives for this section include
- Be familiar with black-body radiators
- Apply Stefan-Boltzmann’s Law to estimate total light output from a radiator
- Apply Wien’s Displacement Law to estimate the peak wavelength (or frequency) of the output from a black body radiator
- Understand the Rayleigh-Jeans Law and how it fails to properly model black-body radiation
All normal matter at temperatures above absolute zero emits electromagnetic radiation, which represents a conversion of a body's internal thermal energy into electromagnetic energy, and is therefore called thermal radiation. Conversely, all normal matter absorbs electromagnetic radiation to some degree. An object that absorbs ALL radiation falling on it, at all wavelengths, is called a blackbody. When a blackbody is at a uniform temperature, its emission has a characteristic frequency distribution that depends on the temperature. This emission is called blackbody radiation.
A room temperature blackbody appears black, as most of the energy it radiates is infra-red and cannot be perceived by the human eye. Because the human eye cannot perceive light waves at lower frequencies, a black body, viewed in the dark at the lowest just faintly visible temperature, subjectively appears grey, even though its objective physical spectrum peaks in the infrared range. When it becomes a little hotter, it appears dull red. As its temperature increases further it becomes yellow, white, and ultimately blue-white.

Blackbody radiation has a characteristic, continuous frequency spectrum that experimentally depends only on the body's temperature. In fact, we can be much more precise:
A body emits radiation at a given temperature and frequency exactly as well as it absorbs the same radiation.
This statement was proved by Gustav Kirchhoff: the essential point is that if we instead suppose a particular body can absorb better than it emits, then in a room full of objects all at the same temperature, it will absorb radiation from the other bodies better than it radiates energy back to them. This means it will get hotter, and the rest of the room will grow colder, contradicting the second law of thermodynamics. Thus, a body must emit radiation exactly as well as it absorbs the same radiation at a given temperature and frequency in order to not violate the second law of thermodynamics.
Any body at any temperature above absolute zero will radiate to some extent, the intensity and frequency distribution of the radiation depending on the detailed structure of the body. To begin analyzing heat radiation, we need to be specific about the body doing the radiating: the simplest possible case is an idealized body which is a perfect absorber, and therefore also (from the above argument) a perfect emitter. So how do we construct a perfect absorber in the laboratory? In 1859 Kirchhoff had a good idea: a small hole in the side of a large box is an excellent absorber, since any radiation that goes through the hole bounces around inside, a lot getting absorbed on each bounce, and has little chance of ever getting out again. So, we can do this in reverse: have an oven with a tiny hole in the side, and presumably the radiation coming out the hole is as good a representation of a perfect emitter as we’re going to find (Figure 1.1.2 ).
By the 1890’s, experimental techniques had improved sufficiently that it was possible to make fairly precise measurements of the energy distribution of blackbody radiation. In 1895, at the University of Berlin, Wien and Lummer punched a small hole in the side of an otherwise completely closed oven, and began to measure the radiation coming out. The beam coming out of the hole was passed through a diffraction grating, which sent the different wavelengths/frequencies in different directions, all towards a screen. A detector was moved up and down along the screen to find how much radiant energy was being emitted in each frequency range. They found a radiation intensity/frequency curve close to the distributions in Figure 1.1.3 .
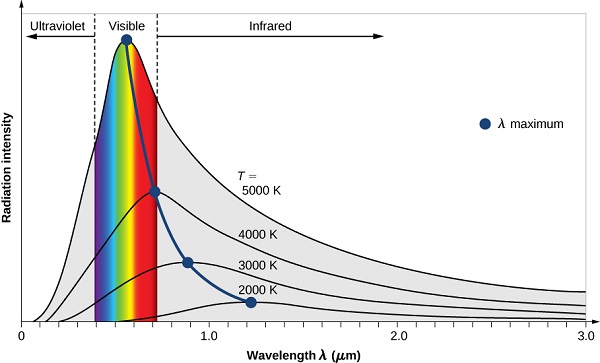
By measuring the blackbody emission curves at different temperatures (Figure 1.1.3 ), they were also able to construct two important phenomenological Laws (i.e., formulated from experimental observations, not from basic principles of nature): Stefan-Boltzmann’s Law and Wien’s Displacement Law.
The radiation of a blackbody radiator is produced by the thermal activity of the material, not the nature of the material, nor how it got thermally excited. Some examples of blackbodies include incandescent light bulbs, stars, and hot stove tops. The emission appears as a continuous spectrum (Figure 1.1.3 ) with multiple coexisting colors. However, not every radiator is a blackbody radiator. For example, the emission of a fluorescence bulb is not one. The following spectrum show the distribution of light from a fluoresce light tube and is a mixture of discrete bands at different wavelengths of light in contrast to the continuous spectra in Figure 1.1.3 for blackbody radiators.
Fluorescent light bulbs contain a mixture of inert gases (usually argon and neon) together with a drop of mercury at low pressure. A different mix of visible colors blend to produce a light that appears to us white with different shadings.
The Stefan-Boltzmann Law
The first quantitative conjecture based on experimental observations was the Stefan-Boltzmann Law (1879) which states the total power (i.e., integrated over all emitting frequencies in Figure 1.1.3 ) radiated from one square meter of black surface goes as the fourth power of the absolute temperature (Figure 1.1.4 ):
\[P = \sigma T^4 \label{Eq1} \]
where
- \(P\) is the total amount of radiation emitted by an object per square meter (\(Watts/ m^{2}\))
- \(\sigma\) is a constant called the Stefan-Boltzman constant (\(5.67 \times 10^{-8}\, Watts\; m^{-2} K^{-4}\))
- \(T\) is the absolute temperature of the object (in K)
The Stefan-Boltzmann Law is easily observed by comparing the integrated value (i.e., under the curves) of the experimental black-body radiation distribution in Figure 1.1.3 at different temperatures. In 1884, Boltzmann derived this \(T^4\) behavior from theory by applying classical thermodynamic reasoning to a box filled with electromagnetic radiation, using Maxwell’s equations to relate pressure to energy density. That is, the tiny amount of energy coming out of the hole (Figure 1.1.2 ) would of course have the same temperature dependence as the radiation intensity inside.
The sun’s surface temperature is 5700 K.
- How much power is radiated by the sun?
- Given that the distance to earth is about 200 sun radii, what is the maximum power possible from a one square kilometer solar energy installation?
Solution
(a) First, we calculate the area of the sun followed by the flux (power). The sun has a radius of \( 6.96 \times 10^{8} m \)
The area of the sun is \( A = 4 \pi R^{2} \).
\[ \begin{align*} A &= 4 (3.1416)(6.96 \times 10^{8} m)^{2} \\[4pt] &= 6.08 \times 10^{18} m^2 \end{align*} \nonumber \]
The power radiated from the sun (via Stefan-Boltzmann Law) is \(P = \sigma T^{4}\) (Equation \ref{Eq1}).
\[ \begin{align*} P &= (5.67 \times 10^{-8}\, Watts\; m^{-2} K^{-4})(5700 K)^{4} \\[4pt] &= 5.98 \times 10^{7} Watts/m^2 \end{align*} \nonumber \]
This value is per square meter.
(b) To calculate the total power radiated by the sun is thus:
\[ \begin{align*} P_{total} &= P A = (5.98 \times 10^{7} Watts/m^2)( 6.08 \times 10^{18} m^2) \\[4pt] &= 3.6 \times 10^{26} Watts \end{align*} \nonumber \]
Wien’s Displacement Law
The second phenomenological observation from experiment was Wien’s Displacement Law. Wien's law identifies the dominant (peak) wavelength, or color, of light coming from a body at a given temperature. As the oven temperature varies, so does the frequency at which the emitted radiation is most intense (Figure 1.1.3 ). In fact, that frequency is directly proportional to the absolute temperature:
\[\nu_{max} \propto T \label{Eq2} \]
where the proportionality constant is \(5.879 \times 10^{10} Hz/K\).
Wien himself deduced this law theoretically in 1893, following Boltzmann’s thermodynamic reasoning. It had previously been observed, at least semi-quantitatively, by an American astronomer, Langley. This upward shift in \(\nu_{max}\) with \(T\) is familiar to everyone—when an iron is heated in a fire (Figure 1.1.1 ), the first visible radiation (at around 900 K) is deep red, the lowest frequency visible light. Further increase in \(T\) causes the color to change to orange then yellow, and finally blue at very high temperatures (10,000 K or more) for which the peak in radiation intensity has moved beyond the visible into the ultraviolet.
Another representation of Wien's Law (Equation \(\ref{Eq2}\)) in terms of the peak wavelength of light is
\[\lambda_{max} = \dfrac{b}{T} \label{Eq2a} \]
where \(T\) is the absolute temperature in kelvin and \(b\) is a constant of proportionality called Wien's displacement constant, equal to \(2.89 \times 10^{−3} m\, K\), or more conveniently to obtain wavelength in micrometers, \(b≈2900\; μm \cdot K\). This is an inverse relationship between wavelength and temperature. So the higher the temperature, the shorter or smaller the wavelength of the thermal radiation. The lower the temperature, the longer or larger the wavelength of the thermal radiation. For visible radiation, hot objects emit bluer light than cool objects.
If surface body temperature is 90 °F.
- How much radiant energy in \(W\, m^{-2}\) would your body emit?
- What is the peak wavelength of emitted radiation?
- What is the total radiant energy emitted by your body in Watts? Note: The average adult human male has a body surface area of about 1.9 \(m^2\) and the average body surface area for a woman is about 1.6 \(m^2\).
Solution
(a) 90 °F is 305 K. We use Stefan-Boltzmann Law (Equation \ref{Eq1}). The total amount of radiation emitted will be \( P = \sigma T^4 \).
\[ \begin{align*} P &= (5.67 \times 10^{-8}\, Watts\; m^{-2} K^{-4})(305 K)^4 \\[4pt] &= 491 W\, m^{-2} \end{align*} \nonumber \]
The peak wavelength of emitted radiation is found using Wien's Law:
\[ \begin{align*} \lambda_{max} &= \frac{ 2.898 \times 10^{-3} m \cdot K}{T} \\[4pt] &= \frac{ 2.898 \times 10^{-3} m \cdot K}{305 K} \\[4pt] &= 9.5 \times 10^{-6} m = 9.5 \mu m\end{align*} \nonumber \]
The total radiant energy density in Watts is :
\[ \begin{align*} \text{Energy}_{\text{male}} &= (491 W\, m^{-2})(1.9 m^{2}) = 933 W \\[4pt] \text{Energy}_{\text{female}} &= (491 W\, m^{-2})(1.6 m^{2}) = 786 W \end{align*} \nonumber \]
For example, if the Sun has a surface temperature of 5700 K, what is the wavelength of maximum intensity of solar radiation?
Solution
If we substitute 5700 K for \(T\) in Equation \(\ref{Eq2a}\), we have
\[\begin{align*} λ_{max} &= \dfrac{0.0029}{5700} \\[4pt] &= 5.1 \times 10^{-7} \, m \end{align*} \nonumber \]
Knowing that violet light has a wavelength of about \(4.0 \times 10^{-7}\) meters, yellow about \(5.6 \times 10^{-7}\) meters, and red about \(6.6 \times 10^{-7}\) meters, what can we say about the color of the Sun's peak radiation? The peak wavelength of the Sun's radiation is at a slightly shorter wavelength than the color yellow, so it is a slightly greenish yellow. To see this greenish tinge to the Sun, you would have to look at it from space. It turns out that the Earth's atmosphere scatters some of the shorter waves of sunlight, which shifts its peak wavelength to pure yellow.
Remember that thermal radiation always spans a wide range of wavelengths (Figure 1.1.2 ) and Equation \ref{Eq2a} only specifies the single wavelength that is the peak of the spectrum. So although the Sun appears yellowish-white, when you disperse sunlight with a prism you see radiation with all the colors of the rainbow. Yellow just represents a characteristic wavelength of the emission.
- At what wavelength does the sun emit most of its radiation if it has a temperature of 5,778 K?
- At what wavelength does the earth emit most of its radiation if it has a temperature of 288 K?
- Answer a
-
500 nm
- Answer b
-
10.0 microns
The Rayleigh-Jeans Law
Lord Rayleigh and J. H. Jeans developed an equation which explained blackbody radiation at low frequencies. The equation which seemed to express blackbody radiation was built upon all the known assumptions of physics at the time. The big assumption which Rayleigh and Jean implied was that infinitesimal amounts of energy were continuously added to the system when the frequency was increased. Classical physics assumed that energy emitted by atomic oscillations could have any continuous value. This was true for anything that had been studied up until that point, including things like acceleration, position, or energy. Their resulting Rayleigh-Jeans Law was
\[ \begin{align} d\rho \left( \nu ,T \right) &= \rho_{\nu} \left( T \right) d\nu \\[4pt] &= \dfrac{8 \pi k_B T}{c^3} \nu^2 d\nu \label{Eq3} \end{align} \]
Experimental data performed on the black box showed slightly different results than what was expected by the Rayleigh-Jeans law (Figure 1.1.5 ). The law had been studied and widely accepted by many physicists of the day, but the experimental results did not lie, something was different between what was theorized and what actually happens. The experimental results showed a bell type of curve, but according to the Rayleigh-Jeans law the frequency diverged as it neared the ultraviolet region (Equation \(\ref{Eq3}\)). Ehrenfest later dubbed this the "ultraviolet catastrophe". It is important to emphasizing that Equation \(\ref{Eq3}\) is a classical result: the only inputs are classical dynamics and Maxwell’s electromagnetic theory.
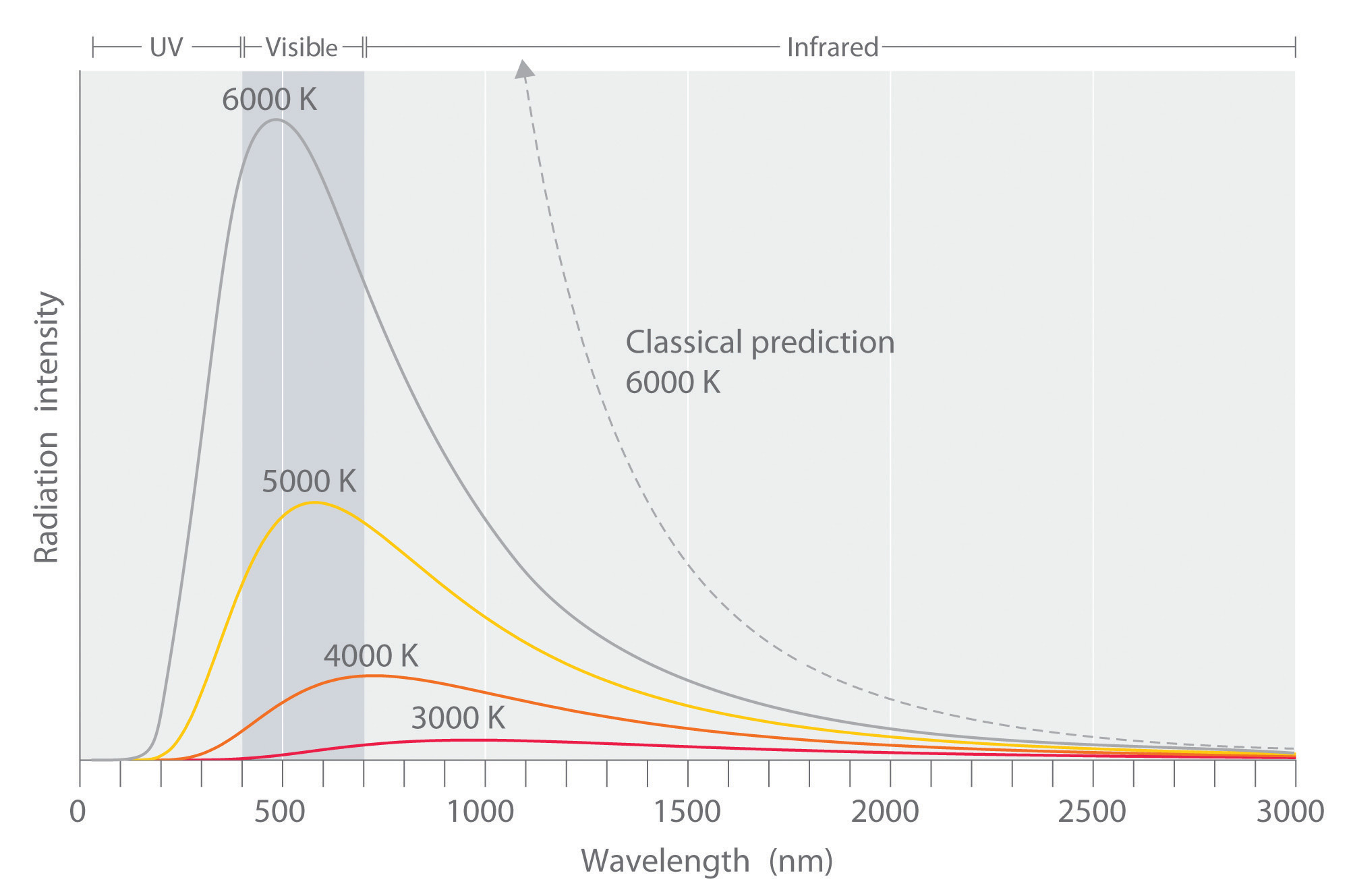
Radiation is understood as a continuous distribution of amplitude vs. wavelength or, equivalently, amplitude vs. frequency (Figure 1.1.5 ). According to Rayleigh-Jeans law, the intensity at a specific frequency \(\nu\) and temperature is
\[\rho(\nu,T) = \dfrac{8\pi k_bT\nu^2}{c^3} \text{.} \nonumber \]
However, in practice, we are more interested in frequency intervals. An exact frequency is the limit of a sequence of smaller and smaller intervals. If we make the assumption that, for a sufficiently small interval, \(ρ(\nu,T)\) does not vary, we get your definition for the differential \(dρ(ν,T)\) in Equation \ref{Eq3}:
The assumption is fair due to the continuity of \(ρ(\nu,T)\). This is the approximation of an integral on a very small interval \(d\nu\) by the height of a point inside this interval (\(\frac{8\pi k_bT\nu^2}{c^3}\)) times its length (\(d\nu\)). So, if we sum an infinite amount of small intervals like the one above we get an integral. The total radiation between \(\nu_1\) and \(\nu_2\) will be:
\[ \begin{align*} \int_{\nu_1}^{\nu_2}\operatorname{d}\!\rho(\nu,T) &= \int_{\nu_1}^{\nu_2}\rho(\nu, T)\operatorname{d}\!\nu \\[4pt] &= \int_{\nu_1}^{\nu_2}\frac{8\pi k_bT\nu^2}{c^3}\operatorname{d}\!\nu \\[4pt] &= 8 \pi k_b T \frac{v_2^3 - v_1^3}{3 c^3}\text{.} \end{align*} \nonumber \]
Observe that \(ρ(\nu,T)\) is quadratic in \(\nu\).
What is the total spectral radiance of a radiator that follows the Rayleigh-Jeans law for its emission spectrum?
Solution
The total spectral radiance \(\rho_{tot}(T)\) is the combined emission over all possible wavelengths (or equivalently, frequencies), which is an integral over the relevant distribution (Equation \ref{Eq3} for the Rayleigh-Jeans Law).
\[ \begin{align*} \rho_{tot}(T) &= \int_0^\infty d\rho \left( \nu ,T \right) \\[4pt] &= \int_0^\infty \dfrac{8 \pi k_B T}{c^3} \nu^2 d\nu \end{align*} \nonumber \]
but the integral
\[\int_0^\infty x^2\mathrm{d}x \nonumber \]
does not converge. Worse, it is infinite,
\[ \lim_{k\to\infty}\int_0^k x^2\mathrm{d}x = \infty \nonumber \]
Hence, the classically derived Rayleigh-Jeans law predicts that the radiance of a blackbody is infinite. Since radiance is power per angle and unit area, this also implies that the total power and hence the energy a blackbody emitter gives off is infinite, which is patently absurd. This is called the ultraviolet catastrophe because the absurd prediction is caused by the classical law not predicting the behavior at high frequencies/small wavelengths correctly (Figure 1.1.5 ).
Contributors and Attributions
Michael Fowler (Beams Professor, Department of Physics, University of Virginia)
David M. Hanson, Erica Harvey, Robert Sweeney, Theresa Julia Zielinski ("Quantum States of Atoms and Molecules")
Paul Flowers (University of North Carolina - Pembroke), Klaus Theopold (University of Delaware) and Richard Langley (Stephen F. Austin State University) with contributing authors. Textbook content produced by OpenStax College is licensed under a Creative Commons Attribution License 4.0 license. Download for free at http://cnx.org/contents/85abf193-2bd...a7ac8df6@9.110).
- ACuriousMind (StackExchange)

