7.1: Collections of Molecules at or Near Equilibrium
- Page ID
- 11595
As introduced in Chapter 5, the approach one takes in studying a system composed of a very large number of molecules at or near thermal equilibrium can be quite different from how one studies systems containing a few isolated molecules. In principle, it is possible to conceive of computing the quantum energy levels and wave functions of a collection of many molecules (e.g., ten \(Na^+\) ions, ten \(Cl^-\) ions and 550 \(H_2O\) molecules in a volume chosen to simulate a concentration of 1 molar \(NaCl_{(aq)}\)), but doing so becomes impractical once the number of atoms in the system reaches a few thousand or if the molecules have significant intermolecular interactions as they do in condensed-phase systems. Also, as noted in Chapter 5, following the time evolution of such a large number of molecules can be confusing if one focuses on the short-time behavior of any single molecule (e.g., one sees jerky changes in its energy, momentum, and angular momentum). By examining, instead, the long-time average behavior of each molecule or, alternatively, the average properties of a significantly large number of molecules, one is often better able to understand, interpret, and simulate such condensed-media systems. Moreover, most experiments do not probe such short-time dynamical properties of single molecules; instead, their signals report on the behavior of many molecules lying within the range of their detection device (e.g., laser beam, STM tip, or electrode). It is when one want to describe the behavior of collections of molecules under such conditions that the power of statistical mechanics comes into play.
Distribution of Energy Among Levels
One of the most important concepts of statistical mechanics involves how a specified total amount of energy \(E\) can be shared among a collection of molecules and within the internal (rotational, vibrational, electronic) and intermolecular (translational) degrees of freedom of these molecules when the molecules have a means for sharing or redistributing this energy (e.g., by collisions). The primary outcome of asking what is the most probable distribution of energy among a large number \(N\) of molecules within a container of volume \(V\) that is maintained in equilibrium by such energy-sharing at a specified temperature \(T\) is the most important equation in statistical mechanics, the Boltzmann population formula:
\[P_j = \dfrac{\Omega_j \exp(- E_j /kT)}{Q}.\]
This equation expresses the probability \(P_j\) of finding the system (which, in the case introduced above, is the whole collection of \(N\) interacting molecules) in its \(j^{th}\) quantum state, where \(E_j\) is the energy of this quantum state, \(T\) is the temperature in K, \(\Omega_j\) is the degeneracy of the \(j^{th}\) state, and the denominator \(Q\) is the so-called partition function:
\[Q = \sum_j \Omega_j \exp\bigg(- \dfrac{E_j}{kT}\bigg).\]
The classical mechanical equivalent of the above quantum Boltzmann population formula for a system with a total of \(M\) coordinates (collectively denoted \(q\)- they would be the internal and intermolecular coordinates of the \(N\) molecules in the system) and \(M\) momenta (denoted \(p\)) is:
\[P(q,p) = \dfrac{ h^{-M}\exp \bigg(- \dfrac{H(q, p)}{kT}\bigg)}{Q},\]
where \(H\) is the classical Hamiltonian, \(h\) is Planck's constant, and the classical partition function \(Q\) is
\[Q = h^{-M} \int \exp \bigg(- \dfrac{H(q, p)}{kT}\bigg) dq \;dp .\]
This probability density expression, which must integrate to unity, contains the factor of \(h^{-M}\) because, as we saw in Chapter 1 when we learned about classical action, the integral of a coordinate-momentum product has units of Planck’s constant.
Notice that the Boltzmann formula does not say that only those states of one particular energy can be populated; it gives non-zero probabilities for populating all states from the lowest to the highest. However, it does say that states of higher energy \(E_j\) are disfavored by the \(\exp (- E_j /kT)\) factor, but, if states of higher energy have larger degeneracies \(\Omega_j\) (which they usually do), the overall population of such states may not be low. That is, there is a competition between state degeneracy \(\Omega_j\), which tends to grow as the state's energy grows, and \(\exp (-E_j /kT)\) which decreases with increasing energy. If the number of particles \(N\) is huge, the degeneracy \(-\Omega\) grows as a high power (let’s denote this power as \(K\)) of \(E\) because the degeneracy is related to the number of ways the energy can be distributed among the \(N\) molecules. In fact, \(K\) grows at least as fast as \(N\). As a result of \(-\Omega\) growing as \(E^K\), the product function \(P(E) = E^K \exp(-E/kT)\) has the form shown in Fig. 7.1 (for \(K=10\), for illustrative purposes)
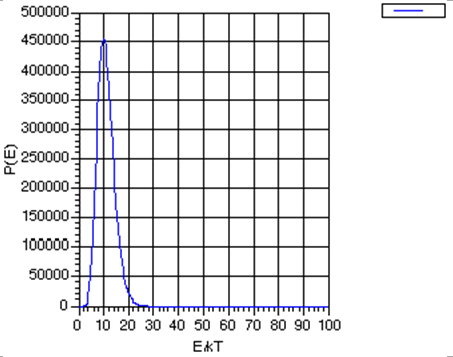
By taking the derivative of this function \(P(E)\) with respect to E, and finding the energy at which this derivative vanishes, one can show that this probability function has a peak at \(E^* = K kT\), and that at this energy value,
\[P(E^*) = (KkT)^K \exp(-K),\]
By then asking at what energy \(E'\) the function \(P(E)\) drops to \(\exp(-1)\) of this maximum value \(P(E^*)\):
\[P(E') = \exp(-1) P(E^*),\]
one finds
\[E' = K kT \bigg(1+ \sqrt{\dfrac{2}{K}} \bigg).\]
So the width of the \(P(E)\) graph, measured as the change in energy needed to cause \(P(E)\) to drop to \(\exp(-1)\) of its maximum value divided by the value of the energy at which \(P(E)\) assumes this maximum value, is
\[\dfrac{E'-E^*}{E^*} = \sqrt{\dfrac{2}{K}}.\]
This width gets smaller and smaller as \(K\) increases.
The primary conclusion is that as the number \(N\) of molecules in the sample grows, which, as discussed earlier, causes \(K\) to grow, the energy probability function becomes more and more sharply peaked about the most probable energy \(E^*\). This, in turn, suggests that we may be able to model, aside from infrequent fluctuations which we may also find a way to take account of, the behavior of systems with many molecules by focusing on the most probable situation (i.e., those having the energy \(E^*\)) and ignoring or making small corrections for deviations from this case.
It is for the reasons just shown that for macroscopic systems near equilibrium, in which \(N\) (and hence \(K\)) is extremely large (e.g., \(N\) ~ \(10^{10}\) to \(10^{24}\)), only the most probable distribution of the total energy among the \(N\) molecules need be considered. This is the situation in which the equations of statistical mechanics are so useful. Certainly, there are fluctuations (as evidenced by the finite width of the above graph) in the energy content of the \(N\)-molecule system about its most probable value. However, these fluctuations become less and less important as the system size (i.e., \(N\)) becomes larger and larger.
Basis of the Boltzmann Population Formula
To understand how this narrow Boltzmann distribution of energies arises when the number of molecules \(N\) in the sample is large, we consider a system composed of \(M\) identical containers, each having volume V, and each made out a material that allows for efficient heat transfer to its surroundings (e.g., through collisions of the molecules inside the volume with the walls of the container) but material that does not allow any of the \(N\) molecules in each container to escape. These containers are arranged into a regular lattice as shown in Figure 7.2 in a manner that allows their thermally conducting walls to come into contact. Finally, the entire collection of \(M\) such containers is surrounded by a perfectly insulating material that assures that the total energy (of all \(N \times M\) molecules) can not change. So, this collection of \(M\) identical containers each containing \(N\) molecules constitutes a closed (i.e., with no molecules coming or going) and isolated (i.e., so total energy is constant) system.
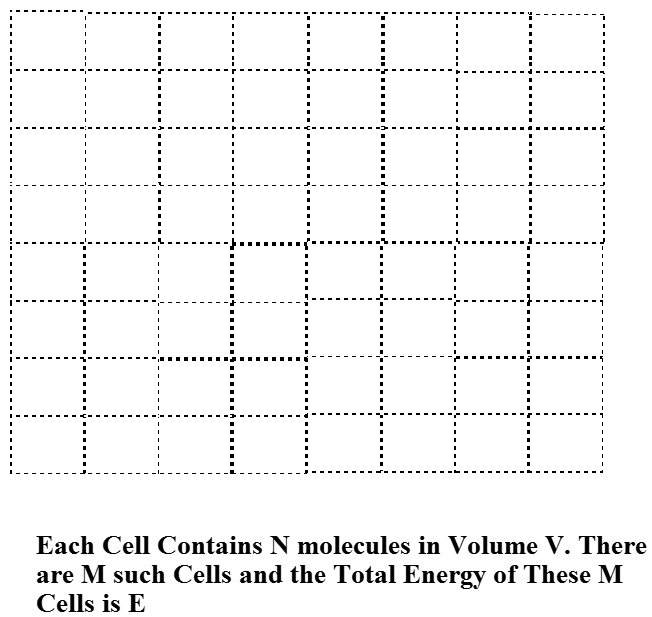
Equal priori Probability Assumption
One of the fundamental assumptions of statistical mechanics is that, for a closed isolated system at equilibrium, all quantum states of the system having energy equal to the energy \(E\) with which the system is prepared are equally likely to be occupied. This is called the assumption of equal a priori probability for such energy-allowed quantum states. The quantum states relevant to this case are not the states of individual molecules, nor are they the states of \(N\) of the molecules in one of the containers of volume \(V\). They are the quantum states of the entire system comprised of \(N\times M\) molecules. Because our system consists of \(M\) identical containers, each with \(N\) molecules in it, we can describe the quantum states of the entire system in terms of the quantum states of each such container. It may seem foolish to be discussing quantum states of the large system containing \(N\times M\) molecules, given what I said earlier about the futility in trying to find such states. However, what I am doing at this stage is to carry out a derivation that is based upon such quantum states but whose final form and final working equations will not actually require one to know or even be able to have these states in hand.
Let’s pretend that we know the quantum states that pertain to \(N\) molecules in a container of volume \(V\) as shown in Figure 7.2, and let’s label these states by an index \(J\). That is \(J=1\) labels the lowest-energy state of \(N\) molecules in the container of volume \(V\), \(J=2\) labels the second such state, and so on. As I said above, I understand it may seem daunting to think of how one actually finds these \(N\)-molecule eigenstates. However, we are just deriving a general framework that gives the probabilities of being in each such state. In so doing, we are allowed to pretend that we know these states. In any actual application, we will, of course, have to use approximate expressions for such energies.
Assuming that the walls that divide the \(M\) containers play no role except to allow for collisional (i.e., thermal) energy transfer among the containers, an energy-labeling for states of the entire collection of \(M\) containers can be realized by giving the number of containers that exist in each single-container J-state. This is possible because, under the assumption about the role of the walls just stated, the energy of each \(M\)-container state is a sum of the energies of the \(M\) single-container states that comprise that \(M\)-container state. For example, if \(M= 9\), the label 1, 1, 2, 2, 1, 3, 4, 1, 2 specifies the energy of this 9-container state in terms of the energies {\(\varepsilon_j\)} of the states of the 9 containers: \(E = 4\varepsilon_1 + 3\varepsilon_2 + \varepsilon_3 + \varepsilon_4\). Notice that this 9-container state has the same energy as several other 9-container states; for example, 1, 2, 1, 2, 1, 3, 4, 1, 2 and 4, 1, 3, 1, 2, 2, 1, 1, 2 have the same energy although they are different individual states. What differs among these distinct states is which box occupies which single-box quantum state.
The above example illustrates that an energy level of the \(M\)-container system can have a high degree of degeneracy because its total energy can be achieved by having the various single-container states appear in various orders. That is, which container is in which state can be permuted without altering the total energy \(E\). The formula for how many ways the \(M\) container states can be permuted such that:
- there are \(n_J\) containers appearing in single-container state \(J\), with
- a total of \(M\) containers, is
\[\Omega(n) = \dfrac{M!}{\prod_Jn_J!}.\]
Here \(n = \{n_1, n_2, n_3, \cdots n_J, \cdots \}\) denote the number of containers existing in single-container states 1, 2, 3, … \(J\), …. This combinatorial formula reflects the permutational degeneracy arising from placing \(n_1\) containers into state 1, \(n_2\) containers into state 2, etc.
If we imagine an extremely large number of containers and we view \(M\) as well as the {\(n_J\)} as being large numbers (n.b., we will soon see that this is the case at least for the most probable distribution that we will eventually focus on), we can ask- for what choices of the variables \(\{n_1, n_2, n_3, \cdots n_J, \cdots \}\) is this degeneracy function \(\Omega(n)\) a maximum? Moreover, we can examine \(\Omega(n)\) at its maximum and compare its value at values of the {\(n\)} parameters changed only slightly from the values that maximized \(\Omega(n)\). As we will see, \(-\Omega\) is very strongly peaked at its maximum and decreases extremely rapidly for values of {\(n\)} that differ only slightly from the optimal values. It is this property that gives rise to the very narrow energy distribution discussed earlier in this Chapter. So, let’s take a closer look at how this energy distribution formula arises.
We want to know what values of the variables \(\{n_1, n_2, n_3, \cdots n_J, \cdots \}\) make \(-\Omega = M!/{\Pi_Jn_J!}\) a maximum. However, all of the \(\{n_1, n_2, n_3, \cdots n_J, \cdots \}\) variables are not independent; they must add up to \(M\), the total number of containers, so we have a constraint
\[\sum_J n_J = M\]
that the variables must obey. The {\(n_j\)} variables are also constrained to give the total energy \(E\) of the \(M\)-container system when summed as
\[\sum_J n_J\varepsilon_J = E.\]
We have two problems: i. how to maximize \(-\Omega\) and ii. how to impose these constraints. Because \(-\Omega\) takes on values greater than unity for any choice of the {\(n_j\)}, \(-\Omega\) will experience its maximum where \(\ln\Omega\) has its maximum, so we can maximize \(\ln \Omega\) if doing so helps. Because the \(n_J\) variables are assumed to take on large numbers (when \(M\) is large), we can use Sterling’s approximation for the natural logarithm of the factorial of a large number:
\[\ln X! \approx X \ln X – X\]
to approximate \(\ln \Omega\) as follows:
\[\ln \Omega \approx \ln M! - \sum_J (n_J \ln n_J – n_J).\]
This expression will prove useful because we can take its derivative with respect to the \(n_J\) variables, which we need to do to search for the maximum of \(\ln \Omega\).
To impose the constraints \(\sum_J n_J = M\) and \(\sum_J n_J \varepsilon_J = E\) we use the technique of Lagrange multipliers. That is, we seek to find values of {\(n_J\)} that maximize the following function:
\[F = \ln M! - \sum_J (n_J \ln n_J – n_J) - \alpha(\sum_Jn_J – M) - \beta(\sum_J n_J \varepsilon_J –E).\]
Notice that this function \(F\) is exactly equal to the \(\ln\Omega\) function we wish to maximize whenever the {\(n_J\)} variables obey the two constraints. So, the maxima of \(F\) and of \(\ln\Omega\) are identical if the {\(n_J\)} have values that obey the constraints. The two Lagrange multipliers \(\alpha\) and \(\beta\) are introduced to allow the values of {\(n_J\)} that maximize \(F\) to ultimately obey the two constraints. That is, we first find values of the {\(n_J\)} variables that make \(F\) maximum; these values will depend on \(\alpha\) and \(\beta\) and will not necessarily obey the constraints. However, we will then choose \(\alpha\) and \(\beta\) to assure that the two constraints are obeyed. This is how the Lagrange multiplier method works.
Lagrange Multiplier Method
Taking the derivative of \(F\) with respect to each independent \(n_K\) variable and setting this derivative equal to zero gives:
\[- \ln n_K - \alpha - \beta \varepsilon_K = 0.\]
This equation can be solved to give \(n_K = \exp(- \alpha) \exp(- \beta \varepsilon_K)\). Substituting this result into the first constraint equation gives \(M = \exp(- \alpha) \sum_J \exp(- \beta \varepsilon_J)\), which allows us to solve for
\(\exp(- \alpha)\) in terms of \(M\). Doing so, and substituting the result into the expression for \(n_K\) gives:
\[n_K = M\dfrac{\exp(- \beta \varepsilon_K)}{Q}\]
where
\[Q = \sum_J \exp(- \beta \varepsilon_J).\]
Notice that the \(n_K\) are, as we assumed earlier, large numbers if \(M\) is large because \(n_K\) is proportional to \(M\). Notice also that we now see the appearance of the partition function \(Q\) and of exponential dependence on the energy of the state that gives the Boltzmann population of that state.
It is possible to relate the \(\beta\) Lagrange multiplier to the total energy \(E\) of the \(M\) containers by summing the number of containers in the Kth quantum state \(n_K\) multiplied by the energy of that quantum state \(\varepsilon_K\)
\[ \begin{algin*} E &= \sum_K n_K \varepsilon_K \\[4pt] &= M\sum_K \dfrac{\varepsilon_K\exp(- \beta \varepsilon_K)}{Q} \\[4pt] &= - M\left(\frac{∂\ln Q}{∂\beta} \right)_{N,V}. \end{align*}\]
This shows that the average energy of a container, computed as the total energy \(E\) divided by the number \(M\) of such containers can be computed as a derivative of the logarithm of the partition function \(Q\). As we show in the following Section of this Chapter, all thermodynamic properties of the \(N\) molecules in the container of volume \(V\) can be obtained as derivatives of the natural logarithm of this \(Q\) function. This is why the partition function plays such a central role in statistical mechanics.
To examine the range of energies over which each of the \(M\) single-container system varies with appreciable probability, let us consider not just the degeneracy \(\Omega(n^*)\) of that set of variables \(\{n^*\} = \{n^*_1, n^*_2, \cdots \}\) that makes \(-\Omega\) maximum, but also the degeneracy \(\Omega(n)\) for values of \(\{n_1, n_2, \cdots\}\) differing by small amounts {\(\delta n_1, \delta n_2, \cdots\)} from the optimal values {\(n^*\)}. Expanding \(\ln \Omega\) as a Taylor series in the parameters \(\{n_1, n_2, \cdots\}\) and evaluating the expansion in the neighborhood of the values {\(n^*\)}, we find:
\[\ln \Omega = \ln \Omega({n^*_1, n^*_2, …}) + \sum_J \left(\frac{∂\ln\Omega}{∂n_J}\right) \delta n_J + \frac{1}{2} \sum_{J,K} \left(\frac{∂^2\ln\Omega}{∂n_J∂n_K}\right) \delta n_J \delta n_K + …\]
We know that all of the first derivative terms (\(\dfrac{∂\ln\Omega}{∂n_J}\)) vanish because \(\ln\Omega\) has been made maximum at {\(n^*\)}. To evaluate the second derivative terms, we first note that the first derivative of \(\ln\Omega\) is
\[\left(\frac{∂\ln\Omega}{∂n_J}\right) = \frac{∂(\ln M! - \sum_J (n_J \ln n_J – n_J))}{∂n_J} = -\ln(n_J).\]
So the second derivatives needed to complete the Taylor series through second order are:
\[\left(\frac{∂^2\ln\Omega}{∂n_J∂nK}\right) = - \frac{\delta_{J,K}}{n_j}.\]
Using this result, we can expand \(\Omega(n)\) in the neighborhood of {\(n^*\)} in powers of \(\delta n_J = n_J-n_J^*\) as follows:
\[\ln \Omega(n) = \ln \Omega(n^*) – \frac{1}{2} \frac{\sum_J (\delta n_J)^2}{n_J^*},\]
or, equivalently,
\[\Omega(n) = \Omega(n^*) \frac{\exp[-\frac{1}{2}\sum_J (\delta n_J)^2]}{n_J^*}\]
This result clearly shows that the degeneracy, and hence, by the equal a priori probability hypothesis, the probability of the \(M\)-container system occupying a state having {\(n_1, n_2, \cdots\)} falls off exponentially as the variables \(n_J\) move away from their most-probable values {\(n^*\)}.
Thermodynamic Limit
As we noted earlier, the \(n_J^*\) are proportional to \(M\) (i.e., \(n_J^* = \dfrac{M\exp(-\beta\varepsilon_J)}{Q} = f_J M\)), so when considering deviations \(\delta n_J\) away from the optimal \(n_J^*\), we should consider deviations that are also proportional to \(M\): \(\delta n_J = M \delta f_J\). In this way, we are treating deviations of specified percentage or fractional amount which we denote \(f_J\). Thus, the ratio \(\dfrac{(\delta n_J)^2}{n_J^*}\) that appears in the above exponential has an M-dependence that allows \(\Omega(n)\) to be written as:
\[\Omega(n) = \Omega(n^*) \exp\left[-\dfrac{M}{2}\sum_J \dfrac{(\delta f_J)^2}{f_J^*}\right],\]
where \(f_J^*\) and \(\delta f_J\) are the fraction and fractional deviation of containers in state \(J\): \(f_J^* = \dfrac{n_J^*}{M}\) and \(\delta f_J = \dfrac{\delta n_J}{M}\). The purpose of writing \(\Omega(n)\) in this manner is to explicitly show that, in the so-called thermodynamic limit, when \(M\) approaches infinity, only the most probable distribution of energy {\(n^*\)} need to be considered because only {\(\delta f_J=0\)} is important as \(M\) approaches infinity.
Fluctuations
Let’s consider this very narrow distribution issue a bit further by examining fluctuations in the energy of a single container around its average energy \(E_{\rm ave} = \dfrac{E}{M}\). We already know that the number of containers in a given state \(K\) can be written as \(n_K = \dfrac{M\exp(- \beta \varepsilon_K)}{Q}\). Alternatively, we can say that the probability of a container occupying the state \(J\) is:
\[p_J = \dfrac{\exp(- \beta \varepsilon_K)}{Q}.\]
Using this probability, we can compute the average energy \(E_{\rm ave}\) as:
\[E_{\rm ave} = \sum_J p_J \varepsilon_J = \dfrac{\sum_J \varepsilon_J \exp(- \beta \varepsilon_K)}{Q} = - \left(\dfrac{∂\ln Q}{∂\beta} \right)_{N,V}.\]
To compute the fluctuation in energy, we first note that the fluctuation is defined as the average of the square of the deviation in energy from the average:
\[(E-E_{\rm ave})^2_{\rm ave} = \sum_J (\varepsilon_J –E_{\rm ave})^2 p_J = \sum_J p_J (\varepsilon_J^2 - 2\varepsilon_J E_{\rm ave} +E_{\rm ave}^2) = \sum_J p_J(\varepsilon_J^2 – E_{\rm ave}^2).\]
The following identity is now useful for further re-expressing the fluctuations:
\[\left(\dfrac{∂^2\ln Q}{∂\beta^2}\right)_{N,V} = \dfrac{ ∂\left( -\sum_J\dfrac{\varepsilon_J \exp(-\beta\varepsilon_J)}{Q} \right) }{∂\beta}\]
\[= \sum_J \dfrac{\varepsilon_J^2\exp(-\beta\varepsilon_J)}{Q} - \left(\sum_J \dfrac{\varepsilon_J\exp(-\beta\varepsilon_J)}{Q}\right) \left(\sum_L \dfrac{\varepsilon_L\exp(-\beta\varepsilon_L)}{Q}\right)\]
Recognizing the first factor immediately above as \(\sum_J \varepsilon_J^2 p_J\), and the second factor as \(- E_{\rm ave}^2\), and noting that \(\sum_J p_J = 1\), allows the fluctuation formula to be rewritten as:
\[(E-E_{\rm ave})^2_{\rm ave} = \left(\dfrac{∂^2\ln Q}{∂\beta^2}\right )_{N,V} = - \left(\dfrac{∂E_{\rm ave}}{∂\beta}\right)_{N,V}.\]
Because the parameter \(\beta\) can be shown to be related to the Kelvin temperature \(T\) as \(\beta =\dfrac{1}{kT}\), the above expression can be re-written as:
\[(E-E_{\rm ave})^2_{\rm ave} = - \left(\dfrac{∂ E_{\rm ave}}{∂\beta}\right)_{N,V} = kT^2 \left(\dfrac{∂E_{\rm ave}}{∂T}\right)_{N,V}.\]
Recognizing the formula for the constant-volume heat capacity
\[C_V = \left(\dfrac{∂E_{\rm ave}}{∂T}\right)_{N,V}\]
allows the fractional fluctuation in the energy around the mean energy \(E_{\rm ave} = \dfrac{E}{M}\) to be expressed as:
\[\dfrac{(E-E_{\rm ave})^2_{\rm ave}}{E_{\rm ave}^2} = \dfrac{kT^2 C_V}{E_{\rm ave}^2}.\]
What does this fractional fluctuation formula tell us? On its left-hand side it gives a measure of the fractional spread of energies over which each of the containers ranges about its mean energy \(E_{\rm ave}\). On the right side, it contains a ratio of two quantities that are extensive properties, the heat capacity and the mean energy. That is, both \(C_V\) and \(E_{\rm ave}\) will be proportional to the number \(N\) of molecules in the container as long as \(N\) is reasonably large. However, because the right-hand side involves \(C_V/E_{\rm ave}^2\), it is proportional to \(N-1\) and thus will be very small for large \(N\) as long as \(C_V\) does not become large. As a result, except near so-called critical points where the heat capacity does indeed become extremely large, the fractional fluctuation in the energy of a given container of \(N\) molecules will be very small (i.e., proportional to \(N-1\)). This finding is related to the narrow distribution in energies that we discussed earlier in this section.
Let’s look at the expression
\[\dfrac{(E-E_{\rm ave})^2_{\rm ave}}{E_{\rm ave}^2} = \frac{kT^2 C_V}{E_{\rm ave}^2}\]
in a bit more detail for a system that is small but still contains quite a few particles-a cluster of \(N\) Ar atoms at temperature \(T\). If we assume that each of the Ar atoms in the cluster has \(\dfrac{3}{2} kT\) of kinetic energy and that the potential energy holding the cluster together is small and constant (so it cancels in \(E-E_{\rm ave}\)), \(E_{\rm ave}\) will be \(\dfrac{3}{2}NkT\) and \(C_V\) will be \(\dfrac{3}{2} Nk\). So,
\[\frac{(E-E_{\rm ave})^2_{\rm ave}}{E_{\rm ave}^2} = \frac{kT^2 C_V}{E_{\rm ave}^2} = kT^2 \dfrac{\dfrac{3}{2}Nk}{\bigg(\dfrac{3}{2} NkT\bigg)^2} = \frac{2}{3 N}.\]
In a nano-droplet of diameter 100 Å, with each Ar atom occupying a volume of ca. \(4/3 \pi (3.8Å)^3 = 232 Å^3\), there will be ca.
\[N = \frac{4}{3} \pi \dfrac{100^3}{\dfrac{4}{3} \pi 3.83} = 1.8 \times10^4\]
Ar atoms. So, the average fractional spread in the energy
\[\sqrt{\frac{(E-E_{\rm ave})^2_{\rm ave}}{E_{\rm ave}^2}} = \sqrt{\frac{2}{3 N}}=0.006.\]
That is, even for a very small nano-droplet, the fluctuation in the energy of the system is only a fraction of a percent (assuming \(C_V\) is not large as near a critical point). This example shows why it is often possible to use thermodynamic concepts and equations even for very small systems, albeit realizing that fluctuations away from the most probable state are more important than in much larger systems.
Partition Functions and Thermodynamic Properties
Let us now examine how this idea of the most probable energy distribution being dominant gives rise to equations that offer molecular-level expressions for other thermodynamic properties. The first equation is the fundamental Boltzmann population formula that we already examined:
\[P_j = \dfrac{\exp(- E_j /kT)}{Q},\]
which expresses the probability for finding the \(N\)-molecule system in its \(J^{\rm th}\) quantum state having energy \(E_j\). Sometimes, this expression is written as
\[P_j = \dfrac{\Omega_j \exp(- E_j /kT)}{Q}\]
where now the index \(j\) is used to label an energy level of the system having energy \(E_j\) and degeneracy. It is important for the student to be used to either notation; a level is just a collection of those states having identical energy.
System Partition Functions
Using this result, it is possible to compute the average energy \(E_{\rm ave}\), sometimes written as \(\langle E \rangle\), of the system
\[\langle E \rangle = \sum_j P_j E_j ,\]
and, as we saw earlier in this Chapter, to show that this quantity can be recast as
\[\langle E \rangle = kT^2 \left(\frac{∂\ln Q}{∂T}\right)_{N,V} .\]
To review how this proof is carried out, we substitute the expressions for \(P_j\) and for \(Q\) into the expression for \(\langle E \rangle\) (I will use the notation labeling energy levels rather than energy states to allow the student to become used to this)
\[\langle E \rangle = \frac{\sum_j E_j \Omega_j \exp(-E_j/kT)}{\sum_I \Omega_I\exp(-E_l/kT)}.\]
By noting that \(\dfrac{∂ (\exp(-E_j/kT))}{∂T} = \dfrac{1}{kT^2} E_j \exp(-E_j/kT)\), we can then rewrite \(\langle E \rangle\) as
\[\langle E \rangle = kT^2 \frac{\sum_j \Omega_j \dfrac{∂ (\exp(-E_j/kT))}{∂T} }{\sum_I \Omega_I\exp(-E_l/kT)}.\]
And then recalling that \(\dfrac{∂X/∂T}{X} = \dfrac{∂\ln X}{∂T}\), we finally obtain
\[\langle E \rangle = kT^2 \left(\frac{∂\ln Q}{∂T}\right)_{N,V}.\]
All other equilibrium properties can also be expressed in terms of the partition function \(Q\). For example, if the average pressure \(\langle p \rangle\) is defined as the pressure of each quantum state (defined as how the energy of that state changes if we change the volume of the container by a small amount)
\[p_j = \bigg(\frac{∂E_j}{∂V}\bigg)_N\]
multiplied by the probability \(P_j\) for accessing that quantum state, summed over all such states, one can show, realizing that only \(E_j\) (not \(T\) or \(W\)) depend on the volume \(V\), that
\[\langle p \rangle = \sum_j \bigg(\frac{∂E_j}{∂V}\bigg)\dfrac{N \Omega_j \exp(- E_j /kT)}{Q}\]
\[= kT\left(\frac{∂\ln Q}{∂V}\right)_{N,T} .\]
If you wonder why the energies \(E_J\) should depend on the volume \(V\), think of the case of \(N\) gas-phase molecules occupying the container of volume V. You know that the translational energies of each of these \(N\) molecules depend on the volume through the particle-in-a-box formula
\[E_{n_x,n_y,n_z}=\dfrac{\hbar^2}{8mL^2}(n_x^2+n_y^2+n_z^2).\]
Changing \(V\) can be accomplished by changing the box length \(L\). This makes it clear why the energies do indeed depend on the volume \(V\). Of course, there are additional sources of the V-dependence of the energy levels. For example, as one shrinks \(V\), the molecules become more crowded, so their intermolecular energies also change.
Without belaboring the point further, it is possible to express all of the usual thermodynamic quantities in terms of the partition function \(Q\). The average energy and average pressure are given above, as is the heat capacity. The average entropy is given as
\[\langle S\rangle = k \ln Q + kT \left(\frac{∂\ln Q}{∂N}\right)_{V,T}\]
the Helmholtz free energy A is
\[A = -kT \ln Q\]
and the chemical potential \(\mu\) is expressed as follows:
\[\mu = -kT \left(\frac{∂\ln Q}{∂N}\right)_{T,V}.\]
As we saw earlier, it is also possible to express fluctuations in thermodynamic properties in terms of derivatives of partition functions and, thus, as derivatives of other properties. For example, the fluctuation in the energy \(\langle (E-\langle E\rangle )^2\rangle\) was shown above to be given by
\[\langle (E-\langle E\rangle )^2\rangle = kT^2 C_V.\]
The text Statistical Mechanics, D. A. McQuarrie, Harper and Row, New York (1977) has an excellent treatment of these topics and shows how all of these expressions are derived.
So, if one were able to evaluate the partition function \(Q\) for \(N\) molecules in a volume \(V\) at a temperature T, either by summing the quantum-level degeneracy and \(\exp(-E_j/kT)\) factors
\[Q = \sum_j \Omega_j \exp(- E_j /kT),\]
or by carrying out the phase-space integral over all \(M\) of the coordinates and momenta of the system
\[Q = h^{-M} \int \exp \bigg(- \dfrac{H(q, p)}{kT}\bigg) dq \; dp ,\]
one could then use the above formulas to evaluate any thermodynamic properties and their fluctuations as derivatives of \(\ln Q\).
The averages discussed above, derived using the probabilities \(p_J = \dfrac{\Omega_J \exp(- E_J /kT)}{Q}\) associated with the most probable distribution, are called ensemble averages with the set of states associated with the specified values of \(N\), \(V\), and \(T\) constituting what is called a canonical ensemble. Averages derived using the probabilities \(\Pi_J\) = constant for all states associated with specified values of \(N\), \(V\), and \(E\) are called ensemble averages for a microcanonical ensemble. There is another kind of ensemble that is often used in statistical mechanics; it is called the grand canonical ensemble and relates to systems with specified volume \(V\), temperature \(T\), and chemical potential \(\mu\) (rather than particle number \(N\)). To obtain the partition function (from which all thermodynamic properties are obtained) in this case, one considers maximizing the same function
\[\Omega(n) = \dfrac{M!}{\prod_Jn_J!}\]
introduced earlier, but now considering each quantum (labeled J) as having an energy \(E_J(N,V)\) that depends on the volume and on how may particles occupy this volume. The variables \(n_J(N)\) are now used to specify how many of the containers introduced earlier contain \(N\) particles and are in the \(J^{\rm th}\) quantum state. These variables have to obey the same two constraints as for the canonical ensemble
\[\sum_J,N n_J(N) = M\]
\[\sum_J,N n_J(N) \varepsilon_J(N,V) =E,\]
but they also are required to obey
\[\sum_{J,N} N n_J(N) = N_{\rm total}\]
which means that the sum adds up to the total number of particles in the isolated system’s large container that was divided into M smaller container. In this case, the walls separating each small container are assumed to allow for energy transfer (as in the canonical ensemble) and for molecules to move from one container to another (unlike the canonical ensemble). Using Lagrange multipliers as before to maximize \(\ln\Omega(n)\) subject to the above three constraints involves maximizing
\[F = \ln M!-\sum_{J,N} (n_{J,N} \ln n_{J,N} – n_{J,N}) - \alpha(\sum_{J,N} n_{J,N} – M) -\beta(\sum_{J,N} n_{J,N} \varepsilon_J –E) –\gamma(\sum_{J,N} N n_{J,N}(N) - N_{\rm total})\]
and gives
\[- \ln n_{K,N} - \alpha - \beta \varepsilon_K -\gamma N = 0\]
or
\[n_{K,N} = \exp[- \alpha - \beta \varepsilon_K -\gamma N].\]
Imposing the first constraint gives
\[M = \sum_{K,N}\exp[- \alpha - \beta \varepsilon_K -\gamma N],]\]
or
\[\exp(-\alpha)=\frac{M}{\sum_{K,N}\exp(-\beta\varepsilon_K(N)-\gamma N)}=\frac{M}{Q(\gamma,V,T)}\]
where the partition function \(Q\) is defined by the sum in the denominator. So, now the probability of the system having \(N\) particles and being in the \(K^{\rm th}\) quantum state is
\[P_K(N)=\frac{\exp(-\beta\varepsilon_K(N)-\gamma N)}{Q}.\]
Very much as was shown earlier for the canonical ensemble, one can then express thermodynamic properties (e.g., \(E\), \(C_V\), etc.) in terms of derivatives of \(\ln Q\). The text Statistical Mechanics, D. A. McQuarrie, Harper and Row, New York (1977) goes through these derivations in good detail, so I will not repeat them here because we showed how to do so when treating the canonical ensemble. To summarize them briefly, one again uses \(\beta = \dfrac{1}{kT}\), finds that g is related to the chemical potential \(\mu\) as
\[\gamma = - \mu \beta\]
and obtains
\[p=\sum_{N,K} P_K(N)\left(\frac{-\partial \varepsilon_K(N,V)}{\partial V}\right)_N=kT \left(\frac{-\partial Q}{\partial V}\right)_{\mu,T}\]
\[N_{\rm ave}=\sum_{N,K} N P_K(N)=kT \left(\frac{-\partial Q}{\partial \mu}\right)_{V,T}\]
\[S=kT\left(\frac{-\partial Q}{\partial T}\right)_{\mu,V}=k\ln Q\]
\[E=\sum_{N,K} \varepsilon_K(N)P_K(N)=kT^2 \left(\frac{-\partial Q}{\partial T}\right)_{\mu,V}\]
\[Q=\sum_{N,K} \exp(-\beta\varepsilon_K(N)+\mu\beta N).\]
The formulas look very much like those of the canonical ensemble, except for the result expressing the average number of molecules in the container Nave in terms of the derivative of the partition function with respect to the chemical potential \(\mu\).
In addition to the equal a priori probability postulate stated earlier (i.e., that, in the thermodynamic limit (i.e., large \(N\)), every quantum state of an isolated system in equilibrium having fixed \(N\), \(V\), and \(E\) is equally probable), statistical mechanics makes another assumption. It assumes that, in the thermodynamic limit, the ensemble average (e.g., using equal probabilities \(\Pi_J\) for all states of an isolated system having specified \(N\), \(V\), and \(E\) or using \(P_j = \dfrac{\exp(- E_j /kT)}{Q}\) for states of a system having specified \(N\), \(V\), and \(T\) or using \(P_K(N)=\dfrac{\exp(-\beta\varepsilon_K(N,V)+\mu\beta N)}{Q}\) for the grand canonical case) of any quantity is equal to the long-time average of this quantity (i.e., the value one would obtain by monitoring the dynamical evolution of this quantity over a very long time). This second postulate implies that the dynamics of an isolated system spends equal amounts of time in every quantum state that has the specified \(N\), \(V\), and \(E\); this is known as the ergodic hypothesis.
Let’s consider a bit more what the physical meaning or information content of partition functions is. Canonical ensemble partition functions represent the thermal-averaged number of quantum states that are accessible to the system at specified values of \(N\), \(V\), and \(T\). This can be seen best by again noting that, in the quantum expression,
\[Q = \sum_j \Omega_j \exp\bigg(- \dfrac{E_j}{kT}\bigg)\]
the partition function is equal to a sum of the number of quantum states in the jth energy level multiplied by the Boltzmann population factor \(\exp(-E_j/kT)\) of that level. So, \(Q\) is dimensionless and is a measure of how many states the system can access at temperature \(T\). Another way to think of \(Q\) is suggested by rewriting the Helmholtz free energy definition given above as \(Q = \exp(-A/kT)\). This identity shows that \(Q\) can be viewed as the Boltzmann population, not of a given energy \(E\), but of a specified amount of free energy \(A\).
For the microcanonical ensemble, the probability of occupying each state that has the specified values of \(N\), \(V\), and \(E\) is equal
\[P_J = \dfrac{1}{\Omega(N,V, E)}\]
where \(\Omega(N,V, E)\) is the total number of such states. In the microcanonical ensemble case, \(\Omega(N,V, E)\) plays the role that \(Q\) plays in the canonical ensemble case; it gives the number of quantum states accessible to the system.
Individual-Molecule Partition Functions
Keep in mind that the energy levels \(E_j\) and degeneracies \(\Omega_j\) and \(\Omega(N,V, E)\) discussed so far are those of the full \(N\)-molecule system. In the special case for which the interactions among the molecules can be neglected (i.e., in the dilute ideal-gas limit) at least as far as expressing the state energies, each of the energies \(E_j\) can be written as a sum of the energies of each individual molecule: \(E_j = \sum_{k=1}^N \varepsilon_j(k)\). In such a case, the above partition function \(Q\) reduces to a product of individual-molecule partition functions:
\[Q = \frac{q_N}{N!} \]
where the N! factor arises as a degeneracy factor having to do with the permutational indistinguishability of the \(N\) molecules (e.g., one must not count both \(\varepsilon_j(3) + \varepsilon_k(7)\) with molecule 3 in state \(j\) and molecule 7 in state \(k\) and \(\varepsilon_j(7) + \varepsilon_k(3)\) with molecule 7 in state \(j\) and molecule 3 in state \(k\); they are the same state), and \(q\) is the partition function of an individual molecule
\[q = \sum_l \omega_l \exp\bigg(-\dfrac{\varepsilon_l}{kT}\bigg).\]
Here, \(\varepsilon_l\) is the energy of the lth level of the molecule and \(\omega_l\) is its degeneracy.
The molecular partition functions \(q\), in turn, can be written as products of translational, rotational, vibrational, and electronic partition functions if the molecular energies \(\varepsilon_l\) can be approximated as sums of such energies. Of course, these approximations are most appropriate to gas-phase molecules whose vibration and rotation states are being described at the lowest level.
The following equations give explicit expressions for these individual contributions to \(q\) in the most usual case of a non-linear polyatomic molecule:
Translational
\[q_t = \left(\frac{2\pi mkT}{\hbar^2}\right)^{\frac{3}{2}} V\]
where \(\mu\) is the mass of the molecule and \(V\) is the volume to which its motion is constrained. For molecules constrained to a surface of area \(A\), the corresponding result is \(q_t = (2\pi mkT/\hbar^2)^{2/2} A\), and for molecules constrained to move along a single axis over a length \(L\), the result is \(q_t = (2\pi mkT/\hbar^2)^{1/2} L\). The magnitudes these partition functions can be computed, using \(\mu\) in amu, \(T\) in Kelvin, and \(L\), \(A\), or \(V\) in cm, cm2 or cm3, as
\[q_t = (3.28 \times10^{13} mT)^{\frac{1}{2},\frac{2}{2},\frac{3}{2}} L, A, V.\]
Clearly, the magnitude of \(q_t\) depends strongly on the number of dimensions the molecule and move around in. This is a result of the vast differences in translational state densities in 1, 2, and 3 dimensions; recall that we encountered these state-density issues in Chapter 2.
Rotational
\[q_{\rm rot} = \frac{\sqrt{\pi}}{\sigma} \sqrt{\frac{8\pi^2I_AkT}{\hbar^2} } \sqrt{\frac{8\pi^2I_BkT}{\hbar^2}} \sqrt{\frac{8\pi^2I_CkT}{\hbar^2}},\]
where \(I_A\), \(I_B\), and \(I_C\) are the three principal moments of inertia of the molecule (i.e., eigenvalues of the moment of inertia tensor). \(\sigma\) is the symmetry number of the molecule defined as the number of ways the molecule can be rotated into a configuration that is indistinguishable from its original configuration. For example, \(\sigma\) is 2 for \(H_2\) or \(D_2\), 1 for \(HD\), 3 for \(NH_3\), and 12 for \(CH_4\). The magnitudes of these partition functions can be computed using bond lengths in Å and masses in amu and \(T\) in \(K\), using
\[\sqrt{\frac{8\pi^2I_AkT}{\hbar^2} } = 9.75 \times10^6 \sqrt{I T}\]
Vibrational
\[q_{\rm vib} = \prod_{k=1}^{3N-6} \left\{\dfrac{\exp(-h\nu_j /2kT)}{1- \exp(-h\nu_j/kT)}\right\},\]
where \(n_j\) is the frequency of the \(j^{\rm th}\) harmonic vibration of the molecule, of which there are \(3N-6\). If one wants to treat the vibrations at a level higher than harmonic, this expression can be modified by replacing the harmonic energies \(h\nu_j\) by higher-level expressions.
Electronic:
\[q_e = \sum_J \omega_J\exp\bigg(-\dfrac{\varepsilon_J}{kT}\bigg),\]
where \(\varepsilon_J\) and \(\omega_J\) are the energies and degeneracies of the \(J^{\rm th}\) electronic state; the sum is carried out for those states for which the product \(\omega_J\exp\bigg(-\dfrac{\varepsilon_J}{kT}\bigg)\) is numerically significant (i.e., levels that any significant thermal population). It is conventional to define the energy of a molecule or ion with respect to that of its atoms. So, the first term in the electronic partition function is usually written as we \(\exp(-D_e/kT)\), where we is the degeneracy of the ground electronic state and \(D_e\) is the energy required to dissociate the molecule into its constituent atoms, all in their ground electronic states.
Notice that the magnitude of the translational partition function is much larger than that of the rotational partition function, which, in turn, is larger than that of the vibrational function. Moreover, note that the 3-dimensional translational partition function is larger than the 2-dimensional, which is larger than the 1-dimensional. These orderings are simply reflections of the average number of quantum states that are accessible to the respective degrees of freedom at the temperature \(T\) which, in turn, relates to the energy spacings and degeneracies of these states.
The above partition function and thermodynamic equations form the essence of how statistical mechanics provides the tools for connecting molecule-level properties such as energy levels and degeneracies, which ultimately determine the \(E_j\) and the \(\Omega_j\), to the macroscopic properties such as \(\langle E\rangle \), \(\langle S\rangle \), \(\langle p\rangle \), \(\mu\), etc.
If one has a system for which the quantum energy levels are not known, it may be possible to express all of the thermodynamic properties in terms of the classical partition function, if the system could be adequately described by classical dynamics. This partition function is computed by evaluating the following classical phase-space integral (phase space is the collection of coordinates \(q\) and conjugate momenta \(p\) as we discussed in Chapter 1)
\[Q = \frac{h^{-NM}}{N!} \int \exp \bigg(- \dfrac{H(q, p)}{kT}\bigg) dq dp.\]
In this integral, one integrates over the internal (e.g., bond lengths and angles), orientational, and translational coordinates and momenta of the \(N\) molecules. If each molecule has \(K\) internal coordinates, 3 translational coordinates, and 3 orientational coordinates, the total number of such coordinates per molecule is \(M = K+6\). One can then compute all thermodynamic properties of the system using this \(Q\) in place of the quantum \(Q\) in the equations given above for \(\langle E\rangle \), \(\langle p\rangle \), etc.
The classical partition functions discussed above are especially useful when substantial intermolecular interactions are present (and, thus, where knowing the quantum energy levels of the \(N\)-molecule system is highly unlikely). In such cases, the classical Hamiltonian is often written in terms of \(H^0\) which contains all of the kinetic energy factors as well as all of the potential energies other than the intermolecular potentials, and the intermolecular potential \(U\), which depends only on a subset of the coordinates: \(H = H^0 + U\). For example, let us assume that \(U\) depends only on the relative distances between molecules (i.e., on the \(3N\) translational degrees of freedom which we denote \(r\)). Denoting all of the remaining coordinates as \(y\), the classical partition function integral can be re-expressed as follows:
\[Q = \frac{h^{-NM}}{N!} \int \exp \bigg(- \dfrac{H^0(y, p)}{kT}\bigg) dy dp \int \exp \bigg(-\dfrac{U(r)}{kT}\bigg) dr.\]
The factor
\[Q_{\rm ideal} = \frac{h^{-NM}}{N!} \int \exp \bigg(- \dfrac{H^0(y, p)}{kT}\bigg) dy dp V^N\]
would be the partition function if the Hamiltonian \(H\) contained no intermolecular interactions \(U\). The \(V^N\) factor arises from the integration over all of the translational coordinates if \(U(r)\) is absent. The other factor
\[Q_{\rm inter} = \frac{1}{V^N} {\int \exp \bigg(-\dfrac{U(r)}{kT}\bigg) dr}\]
contains all the effects of intermolecular interactions and reduces to unity if the potential \(U\) vanishes. If, as the example considered here assumes, \(U\) only depends on the positions of the centers of mass of the molecules (i.e., not on molecular orientations or internal geometries), the \(Q_{\rm ideal}\) partition function can be written in terms of the molecular translational, rotational, and vibrational partition functions shown earlier:
\[Q_{\rm ideal} = \frac{1}{N!} \bigg[\left(\frac{2\pi mkT}{\hbar^2}\right)^{\frac{3}{2}} V \frac{\sqrt{\pi}}{\sigma} \sqrt{\frac{8\pi^2I_AkT}{\hbar^2} } \sqrt{\frac{8\pi^2I_BkT}{\hbar^2}} \sqrt{\frac{8\pi^2I_CkT}{\hbar^2}} \]
\[\prod_{k=1}^{3N-6} \left\{\frac{\exp(-h\nu_j /2kT)}{1- \exp(-h\nu_j/kT)}\right\} \sum_J \omega_J\exp\left(\frac{-\varepsilon_J}{kT}\right)\bigg]^N .\]
Because all of the equations that relate thermodynamic properties to partition functions contain \(\ln Q\), all such properties will decompose into a sum of two parts, one coming from \(\ln Q_{\rm ideal}\) and one coming from \(\ln Q_{\rm inter}\). The latter contains all the effects of the intermolecular interactions. This means that, in this classical mechanics case, all the thermodynamic equations can be written as an ideal component plus a part that arises from the intermolecular forces. Again, the Statistical Mechanics text by McQuarrie is a good source for reading more details on these topics.
Equilibrium Constants in Terms of Partition Functions
One of the most important and useful applications of statistical thermodynamics arises in the relation giving the equilibrium constant of a chemical reaction or for a physical transformation (e.g., adsorption of molecules onto a metal surface or sublimation of molecules from a crystal) in terms of molecular partition functions. Specifically, for any chemical or physical equilibrium (e.g., the former could be the \(HF \rightleftharpoons H^+ + F^-\) equilibrium; the latter could be \(H_2O(l) \rightleftharpoons H_2O(g)\)), one can relate the equilibrium constant (expressed in terms of numbers of molecules per unit volume or per unit area, depending on whether species undergo translational motion in 3 or 2 dimensions) in terms of the partition functions of these molecules. For example, in the hypothetical chemical equilibrium \(A + B \rightleftharpoons C\), the equilibrium constant \(K\) can be written, if the species can be treated as having negligibly weak intermolecular potentials, as:
\[K = \dfrac{(N_C/V)}{(N_A/V) (N_B/V)} = \frac{(q_C/V)}{(q_A/V) (q_B/V)}.\]
Here, \(q_J\) is the partition function for molecules of type \(J\) confined to volume \(V\) at temperature \(T\). As another example consider the isomerization reaction involving the normal (N) and zwitterionic (Z) forms of arginine that were discussed in Chapter 5. Here, the pertinent equilibrium constant would be:
\[K = \frac{(N_Z/V)}{(N_N/V)} = \frac{(q_Z/V)}{(q_N/V)}.\]
So, if one can evaluate the partition functions \(q\) for reactant and product molecules in terms of the translational, electronic, vibrational, and rotational energy levels of these species, one can express the equilibrium constant in terms of these molecule-level properties.
Notice that the above equilibrium constant expressions equate ratios of species concentrations (in, numbers of molecules per unit volume) to ratios of corresponding partition functions per unit volume. Because partition functions are a count of the number of quantum states available to the system (i.e., the average density of quantum states), this means that we equate species number densities to quantum state densities when we use the above expressions for the equilibrium constant. In other words, statistical mechanics produces equilibrium constants related to numbers of molecules (i.e., number densities) not molar or molal concentrations.
Contributors and Attributions
Jack Simons (Henry Eyring Scientist and Professor of Chemistry, U. Utah) Telluride Schools on Theoretical Chemistry
Integrated by Tomoyuki Hayashi (UC Davis)


