1.4: Free Particle Motions in More Dimensions
- Page ID
- 11544
The number of dimensions depends on the number of particles and the number of spatial (and other) dimensions needed to characterize the position and motion of each particle. The number of dimensions also affects the number of quantum numbers that may be used to label eigenstates of the Hamiltonian.
Schrödinger Equation
Consider an electron of mass m and charge \(e\) moving on a two-dimensional surface that defines the \(x,y\) plane (e.g., perhaps an electron is constrained to the surface of a solid by a potential that binds it tightly to a narrow region in the \(z\)-direction but allows it to roam freely over a rectangular area in the \(x,y\) plane), and assume that the electron experiences a constant and not time-varying potential \(V_0\) at all points in this plane. For example, if \(V_0\) is negative, it could reflect the binding energy of the electron relative to its energy in vacuum.
The pertinent time independent Schrödinger equation is:
\[- \dfrac{\hbar^2}{2m} \left(\dfrac{\partial^2}{\partial x^2} +\dfrac{\partial^2}{\partial y^2}\right)\psi(x,y) +V_0 \psi(x,y) = E\psi(x,y).\]
The task at hand is to solve the above eigenvalue equation to determine the allowed energy states for this electron. Because there are no terms in this equation that couple motion in the \(x\) and \(y\) directions (e.g., no terms of the form \(x^ay^b\) or \(x\dfrac{\partial}{\partial y}\) or \(\psi\dfrac{\partial}{\partial x}\)), separation of variables can be used to write \(y\) as a product \(\psi(x,y)=A(x)B(y)\). Substitution of this form into the Schrödinger equation, followed by collecting together all \(x\)-dependent and all y-dependent terms, gives;
\[- \dfrac{\hbar^2}{2m} \frac{1}{A}\frac{\partial^2 A}{\partial x^2} - \dfrac{\hbar^2}{2m} \frac{1}{B}\frac{\partial^2 B}{\partial y^2} = E-V_0.\]
Since the first term contains no \(y\)-dependence and the second contains no \(x\)-dependence, and because the right side of the equation is independent of both \(x\) and \(y\), both terms on the left must actually be constant (these two constants are denoted \(E_x\) and \(E_y\), respectively, realizing that they have units of energy). This observation allows two separate Schrödinger equations to be written:
\[- \dfrac{\hbar^2}{2m} \frac{1}{A}\frac{\partial^2 A}{\partial x^2} = E_x\]
and
\[- \dfrac{\hbar^2}{2m} \frac{1}{B}\frac{\partial^2 B}{\partial y^2} = E_y.\]
The total energy \(E\) can then be expressed in terms of these separate energies \(E_x\) and \(E_y\) from \(E_x + E_y = E-V_0\). Solutions to the \(x-\) and \(y-\) Schrödinger equations are easily seen to be:
\[A(x) = \exp\left(ix\sqrt{\frac{2mE_x}{\hbar^2}}\right) \text{and} \exp\left(-ix\sqrt{\frac{2mE_x}{\hbar^2}}\right)\]
\[B(y) = \exp\left(iy\sqrt{\frac{2mE_y}{\hbar^2}}\right) \text{and} \exp\left(-iy\sqrt{\frac{2mE_y}{\hbar^2}}\right).\]
Two independent solutions are obtained for each equation because the \(x-\) and \(y-\)space Schrödinger equations are both second order differential equations (i.e., a second order differential equation has two independent solutions).
Boundary Conditions
The boundary conditions, not the Schrödinger equation, determine whether the eigenvalues will be discrete or continuous
If the electron is entirely unconstrained within the \(x,y\) plane, the energies \(E_x\) and \(E_y\) can assume any values; this means that the experimenter can inject the electron onto the \(x,y\) plane with any total energy \(E\) and any components \(E_x\) and \(E_y\) along the two axes as long as \(E_x + E_y = E\). In such a situation, one speaks of the energies along both coordinates as being in the continuum or not quantized.
In contrast, if the electron is constrained to remain within a fixed area in the \(x,y\) plane (e.g., a rectangular or circular region), then the situation is qualitatively different. Constraining the electron to any such specified area gives rise to boundary conditions that impose additional requirements on the above \(A\) and \(B\) functions. These constraints can arise, for example, if the potential \(V(x,y)\) becomes very large for \(x,y\) values outside the region, in which case, the probability of finding the electron outside the region is very small. Such a case might represent, for example, a situation in which the molecular structure of the solid surface changes outside the enclosed region in a way that is highly repulsive to the electron (e.g., as in the case of molecular corrals on metal surfaces). This case could then represent a simple model of so-called corrals in which the particle is constrained to a finite region of space.
For example, if motion is constrained to take place within a rectangular region defined by \(0 \le x\le L_x\); \(0 \le y\le L_y\), then the continuity property that all wave functions must obey (because of their interpretation as probability densities, which must be continuous) causes \(A(x)\) to vanish at 0 and at \(L_x\). That is, because \(A\) must vanish for \(x < 0\) and must vanish for \(x > L_x\), and because \(A\) is continuous, it must vanish at \(x = 0\) and at \(x = L_x\). Likewise, \(B(y)\) must vanish at 0 and at \(L_y\). To implement these constraints for \(A(x)\), one must linearly combine the above two solutions \(\exp\left(ix\sqrt{\dfrac{2mE_x}{\hbar^2}}\right)\)and \(\exp\left(-ix\sqrt{\dfrac{2mE_x}{\hbar^2}}\right) \)to achieve a function that vanishes at \(x=0\):
\[A(x) = \exp\left(ix\sqrt{\frac{2mE_x}{\hbar^2}}\right) - \exp\left(-ix\sqrt{\frac{2mE_x}{\hbar^2}}\right).\]
One is allowed to linearly combine solutions of the Schrödinger equation that have the same energy (i.e., are degenerate) because Schrödinger equations are linear differential equations. An analogous process must be applied to \(B(y)\) to achieve a function that vanishes at \(y=0\):
\[B(y) = \exp\left(iy\sqrt{\frac{2mE_y}{\hbar^2}}\right) - \exp\left(-iy\sqrt{\frac{2mE_y}{\hbar^2}}\right).\]
Further requiring \(A(x)\) and \(B(y)\) to vanish, respectively, at \(x=L_x\) and \(y=L_y\), respectively, gives equations that can be obeyed only if \(E_x\) and \(E_y\) assume particular values:
\[ \exp\left( iL_x \sqrt{\frac{2mE_x}{\hbar^2}} \right)-\exp\left(-iL_x\sqrt{\frac{2mE_x}{\hbar^2}}\right)=0\text{, and}\]
\[ \exp \left( iL_y \sqrt{\frac{2mE_y}{\hbar^2}} \right) - \exp \left(-iL_y\sqrt{\frac{2mE_y}{\hbar^2}} \right) = 0.\]
These equations are equivalent (i.e., using \(\exp(ix) = \cos(x) + i \sin(x)\)) to
\[\sin\left(L_x\sqrt{\frac{2mE_x}{\hbar^2}}\right) = \sin\left(L_y\sqrt{\frac{2mE_y}{\hbar^2}}\right) = 0.\]
Knowing that \(\sin(\theta)\) vanishes at \(q = n\pi\), for \(n=1,2,3,\cdots,\) (although the \(\sin(n\pi)\) function vanishes for \(n=0\), this function vanishes for all \(x\) or \(y\), and is therefore unacceptable because it represents zero probability density at all points in space) one concludes that the energies \(E_x\) and \(E_y\) can assume only values that obey:
\[L_x\sqrt{\frac{2mE_x}{\hbar^2}} =n_x\pi,\]
\[L_y\sqrt{\frac{2mE_y}{\hbar^2}} =n_y\pi\]
or
\[E_x = \frac{n_x^2\pi^2 \hbar^2}{2mL_x^2}\]
and
\[E_y = \frac{n_y^2\pi^2 \hbar^2}{2mL_y^2}, \text{ with } n_x \text{ and } n_y =1,2,3, \cdots\]
and
\[E = V_0 +E_x+ E_y.\]
It is important to stress that it is the imposition of boundary conditions, expressing the fact that the electron is spatially constrained, that gives rise to quantized energies. In the absence of spatial confinement, or with confinement only at \(x = 0\) or \(L_x\) or only at \(y = 0\) or \(L_y\), quantized energies would not be realized.
In this example, confinement of the electron to a finite interval along both the \(x\) and \(y\) coordinates yields energies that are quantized along both axes. If the electron were confined along one coordinate (e.g., between \(0 \le x\le L_x\)) but not along the other (i.e., \(B(y)\) is either restricted to vanish only at \(y=0\) or at \(y=L_y\) or at neither point), then the total energy \(E\) lies in the continuum; its \(E_x\) component is quantized but \(E_y\) is not. Analogs of such cases arise, for example, for a triatomic molecule containing one strong and one weak bond. If the bond with the higher dissociation energy is excited to a level that is not enough to break it but that is in excess of the dissociation energy of the weaker bond, one has a situation that is especially interesting. In this case, one has two degenerate states
- one with the strong bond having high internal energy and the weak bond having low energy (\(\psi_1\)), and
- a second with the strong bond having little energy and the weak bond having more than enough energy to rupture it (\(\psi_2\)).
Although an experiment may prepare the molecule in a state that contains only the former component (i.e., \(\Psi(t=0)= C_1\psi_1 + C_2\psi_2\) with \(C_1 = 1\), \(C_2 = 0\)), coupling between the two degenerate functions (induced by terms in the Hamiltonian H that have been ignored in defining \(\psi_1\) and \(\psi_2\)) can cause the true wave function \(\Psi = \exp(-itH/\hbar) \Psi(t=0)\) to acquire a component of the second function as time evolves. In such a case, one speaks of internal vibrational energy relaxation (IVR) giving rise to unimolecular decomposition of the molecule.
Energies and Wave Functions for Bound States
For discrete energy levels, the energies are specified functions that depend on quantum numbers, one for each degree of freedom that is quantized
Returning to the situation in which motion is constrained along both axes, the resultant total energies and wave functions (obtained by inserting the quantum energy levels into the expressions for \(A(x)\) and \(B(y)\)) are as follows:
\[E_x = \frac{n_x^2\pi^2 \hbar^2}{2mL_x^2}\]
and
\[E_y = \frac{n_y^2\pi^2 \hbar^2}{2mL_y^2}\]
\[E = E_x + E_y +V_0\]
\[\psi(x,y) = \sqrt{\frac{1}{2L_x}}\sqrt{\frac{1}{2L_y}}\left[\exp\bigg(\frac{in_x\pi x}{L_x}\bigg) -\exp\bigg(-\frac{in_x\pi x}{L_x}\bigg)\right]\left[\exp\bigg(\frac{in_y\pi y}{L_y}\bigg) -\exp\bigg(-\frac{in_y\pi y}{L_y}\bigg)\right] \]
with \(n_x\) and \(n_y =1,2,3, \cdots\).
The two \(\sqrt{\dfrac{1}{2L}}\) factors are included to guarantee that \(y\) is normalized:
\[\int |\psi(x,y)|^2 dx,dy = 1.\]
Normalization allows \(|\psi(x,y)|^2\) to be properly identified as a probability density for finding the electron at a point \(x\), \(y\).
Shown in Figure 1. 13 are plots of four such two dimensional wave functions for \(n_x\) and \(n_y\) values of (1,1), (2,1), (1.2) and (2,2), respectively.
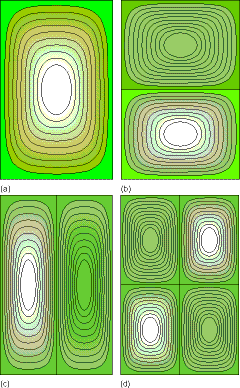
Note that the functions vanish on the boundaries of the box, and notice how the number of nodes (i.e., zeroes encountered as the wave function oscillates from positive to negative) is related to the \(n_x\) and \(n_y\) quantum numbers and to the energy. This pattern of more nodes signifying higher energy is one that we encounter again and again in quantum mechanics and is something the student should be able to use to guess the relative energies of wave functions when their plots are at hand. Finally, you should also notice that, as in the one-dimensional box case, any attempt to classically interpret the probabilities \(P(x,y)\) corresponding to the above quantum wave functions will result in failure. As in the one-dimensional case, the classical \(P(x,y)\) would be constant along slices of fixed \(x\) and varying \(y\) or slices of fixed \(y\) and varying \(x\) within the box because the speed is constant there. However, the quantum \(P(x,y)\) plots, at least for small quantum numbers, are not constant. For large \(P(x,y)\) and ny values, the quantum \(P(x,y)\) plots will again, via the quantum-classical correspondence principle, approach the (constant) classical \(P(x,y)\) form except near the classical turning points (i.e., near the edges of the two-dimensional box).
If, instead of being confined to a rectangular corral, the electron were constrained to lie within a circle of radius R, the Schrödinger equation is more favorably expressed in polar coordinates \((r, \theta)\). Transforming the partial derivatives appearing in the Schrödinger equation
\[- \dfrac{\hbar^2}{2m} (\frac{\partial^2}{\partial x^2} +\frac{\partial^2}{\partial y^2})\psi(x,y) +V(x,y) \psi(x,y) = E\psi(x,y)\]
into polar coordinates and realizing that the potential depends on \(r\) but not on \(\theta\) gives
\[ - \dfrac{\hbar^2}{2m} (\frac{1}{r}\frac{\partial}{\partial r}(r\frac{\partial}{\partial r}) +\frac{1}{r^2} \frac{\partial^2}{\partial \theta^2}) \psi(r, \theta) + V (r) \psi(r, \theta) = E\psi(r, \theta).\]
Again using separation of variables to substitute
\[\psi(r, \theta) = A(r) B(\theta)\]
into the Schrödinger equation and dividing by \(AB\), we obtain
\[- \frac{1}{A} \dfrac{\hbar^2}{2m} (\frac{1}{r}\frac{\partial}{\partial r}(r\frac{\partial}{\partial r})A(r)) +V_0 – \frac{1}{B} \dfrac{\hbar^2}{2m} (\frac{1}{r^2}\frac{\partial^2 B(\theta)}{\partial \theta^2}) = E\]
where \(V_0\) is the value of the potential inside the circular region. The first two terms on the left and the \(E\) on the right side contain no reference to \(\theta\), so the quantity \(\dfrac{1}{B} \dfrac{\partial^2 B(\theta)}{\partial \theta^2}\) must be independent of \(\theta\):
\[\frac{1}{B} \frac{\partial^2 B(\theta)}{\partial \theta^2} = c\]
Moreover, because the coordinates \((r, \theta)\) and \((r, \theta +2\pi)\) describe the same point in space, \(B(\theta)\) must obey
\[B(\theta) = B(\theta +2 \pi).\]
The solutions to the above differential equation for \(B(\theta)\) subject to the periodicity condition are
\[B(\theta) = \frac{1}{\sqrt{2\pi}} \exp(± in \theta); n = 0, 1, 2, ….\]
This means that the equation for the radial part of the wave function is
\[- \frac{1}{A} \dfrac{\hbar^2}{2m} (\frac{1}{r}\frac{\partial}{\partial r}(r\frac{\partial}{\partial r})A(r)) +V_0 – \frac{1}{B}\dfrac{\hbar^2}{2m} (\frac{1}{r^2}n^2) = E\]
or
\[r^2 \frac{d^2A}{dr^2} + r \frac{dA}{dr} –n^2 A +\frac{2mr^2}{\hbar^2} (E-V_0)A = 0 .\]
This differential equation is probably not familiar to you, but it turns out this is the equation obeyed by so-called Bessel functions. The Bessel functions labeled \(J_n(ax)\) obey
\[x^2 \frac{d^2J}{dx^2} +x \frac{dJ}{dx} – n^2 J + a^2 x^2 J = 0\]
so, our \(A\) function is
\[A(r) = J_n\left(\sqrt{\frac{2m(E-V_0)}{\hbar^2}}r\right).\]
The full wave functions are then
\[\psi(r, \theta) = A(r) B(\theta) = N J_n\left(\sqrt{\frac{2m(E-V_0)}{\hbar^2}}r\right) \frac{1}{\sqrt{2\pi}} \exp(± in \theta)\]
where \(N\) is a normalization constant. The energy eigenvalues \(E_{j,n}\) cannot be expressed analytically as in the particle-in-a box system (where we used knowledge of the zeros of the sin function to determine \(E_n\)). However, knowing that \(A(r)\) must vanish at \(R = R\), we can use tables (for example, see Kreyszig, E. Advanced Engineering Mathematics, 8th ed.; John Wiley and Sons, Inc.: New York, 1999) that give the values of \(x\) at which \(J_n(x)\) vanishes to determine the set of eigenvalues associated with each value of the angular momentum quantum number \(n\). In the table shown below, we list the first five values at which \(J_0\), \(J_1\), and \(J_2\) vanish.
Values of \(x\) at which \(J_n(x)\) vanish for \(n = 0, 1\), and \(2\)
If we call the values at which \(J_{n(x)}\) vanishes \(z_{n,j}\), then the energies are given as
\[E_{n,j} = V_0 + \dfrac{(z_{n,j})^2 \hbar^2}{2mR^2}.\]
From the ordering of the \(z_{n,j}\) values shown in the table above, we can see that the ordering of the energy levels will be \(z_{0.1}\), \(z_{1,1}\), \( z_{1,2}\), \(z_{1,0}\), \(z_{1,1}\), \(z_{1,2}\), and so forth, regardless of the size of the circle \(R\) or the mass of the particle \(m\).
The state with \(n = -1\) has the same energy as that with \(n = 1\); likewise, \(n = -2\) has the same energy as \(n=2\). So, all but the \(n = 0\) states are doubly degenerate; the only difference between such pairs of states is the sense of the angular momentum terms \(\exp(\pm ni \theta)\). These energy levels depend on both the angular momentum quantum number \(n\), as well as the radial quantum number \(j\) and they depend upon \(R\) much like the particle-in-a-box energies depend on the box length \(L\). In Figure 1.13a we show plots of the probability densities \(|\psi(r,\theta)|^2\) for \(n = 0, 1\), and \(2\) and for \(j = 1, 3\), and \(5\) to illustrate how the number of radial nodes increases as \(j\) increases.

The character of \(|\psi(r,\theta)|^2\) also changes with \(n\). For \(n = 0\), there is high amplitude for the particle being in the center of the circle, but for \(n > 0\), there is no amplitude in the center. This is analogous to what one finds for atomic orbitals; \(s\) orbitals have non-zero amplitude at the nucleus, but p, d, and higher orbitals do not.
Let’s examine a few more easy problems that can be solved analytically to some degree. This will help illustrate how boundary conditions generate quantization and how the number of quantum numbers depends on the dimensionality of the problem. When considering a particle of mass \(m\) moving in three dimensions but constrained to remain within a sphere of radius R, we replace the three Cartesian coordinates \(x, y,\) and \(z\) by the spherical coordinates \(r\), \(\theta\), and \(\phi\). Doing so, changes the Schrödinger equation’s kinetic energy terms into what we show below
\[-\frac{\hbar^2}{2mr^2}\left(\frac{\partial}{\partial r}\left(r^2\frac{\partial\psi}{\partial r}\right)\right) -\frac{\hbar^2}{2m} \frac{1}{r^2\sin\theta}\frac{\partial}{\partial \theta}\left(\sin\theta\frac{\partial \psi}{\partial\theta}\right) -\frac{\hbar^2}{2m}\frac{1}{r^2\sin\theta}\frac{\partial^2 \psi}{\partial\phi^2}+ V(r)\psi = E\psi.\]
Taking the potential to be \(V_0\) (a constant) for \(0 \le r \le R\), and infinite for \(r > R\), we can again use separation of variables to progress in solving this three dimensional differential equation. We substitute
\[\psi(r,\theta,\phi) = Y_{L,M} (\theta,\phi) F(r)\]
into the Schrödinger equation and taking into account that the so-called spherical harmonic functions \(Y_{L,M} (\theta,\phi)\) obey the following:
\[\frac{1}{\sin\theta}\frac{\partial}{\partial \theta}\left(\sin\theta\frac{\partial Y_{L,M}}{\partial\theta}\right)+ \frac{1}{\sin^2\theta}\frac{\partial^2 Y_{L,M}}{\partial\phi^2}= - L(L+1) Y_{L,M}.\]
This reduces the Schrödinger equation to an equation for the radial function \(F(r)\):
\[-\frac{\hbar^2}{2mr^2}\left(\frac{\partial}{\partial r}\left(r^2\frac{\partial F}{\partial r}\right)\right) + \frac{\hbar^2}{2mr^2}L(L+1)F + V_0 F = EF.\]
Again, this equation is probably not familiar to you, but it can be recast in a way that makes it equivalent to the equation obeyed by so-called spherical Bessel functions
\[ x^2\frac{d^2j_L(x)}{dx^2} +2x \frac{dj_L(x)}{dx} +[x^2 –L(L+1)] j_L(x) = 0\]
by taking
\[x = \sqrt{\frac{2m(E-V_0)}{\hbar^2}} r.\]
The result is that the wave functions for this problem reduce to
\[\psi(r,\theta,\phi) = N Y_{L,M} (\theta,\phi) j_L\bigg(\sqrt{\frac{2m(E-V_0)}{\hbar^2}} r\bigg)\]
where \(N\) is a normalization constant. The energies are determined by requiring \(\psi(r,\theta,\phi)\)
to vanish at \(r = R\), which is analogous to insisting that the spherical Bessel function vanish at \(r = R\) in the earlier problem we studied. The values of \(x (z_{L,n})\) at which \(j_L(x)\) vanish again can be found in various tabulations, including that cited earlier. Several of these values are tabulated below for illustration.
Values of \(x\) at which \(j_L(x)\) vanish for \(L = 0, 1, 2, 3\), and \(4\)
|
n=1 |
n=2 |
n=3 |
n=4 |
|
|---|---|---|---|---|
|
L=0 |
3.142 |
6.283 |
9.425 |
12.566 |
|
L=1 |
4.493 |
7.725 |
10.904 |
14.066 |
|
L=2 |
5.763 |
9.095 |
12.323 |
15.515 |
|
L=3 |
6.988 |
10.417 |
13.698 |
16.924 |
|
L=4 |
8.183 |
11.705 |
15.040 |
18.301 |
From the values of \(z_{L,n}\), one finds the energies from
\[E_{L,n} = V_0 + \frac{(z_{L,n})^2\hbar^2}{2mR^2}.\]
Again, we see how the energy depends on the size of the constraining region (characterized by \(R\)) very much in the same way as in the earlier systems. We also see that \(E\) depends on the angular momentum quantum number \(L\) (much as it did in the preceding example) and on the mass of the particle. However, the energy ordering of these levels is different from what we have seen earlier as reflected in the ordering of the \(z_{L,n}\) values shown in the above table. The energies appear in the order (\(L=0\) \(n=1\); \(L=-2\) \(n=1\); \(L=2\) \(n=1\); \(L=0\) \(n=2\); \(L=3\) \(n=1\); \(L=1\) \(n=2\), and so on, and this is true for any size sphere \(R\) and any particle mass m.
If, instead of being constrained to move within a spherical volume, the particle is constrained to move on the surface of a sphere or radius \(R\), the variable \(R\) is fixed (at \(R = R\)) and the Schrödinger equation becomes
\[-\frac{\hbar^2}{2m} \frac{1}{R^2\sin\theta}\frac{\partial}{\partial \theta}\left(\sin\theta\frac{\partial \psi}{\partial\theta}\right) -\frac{\hbar^2}{2m}\frac{1}{R^2\sin^2\theta}\frac{\partial^2 \psi}{\partial\phi^2}+ V_0\psi = E\psi.\]
Using
\[\frac{1}{\sin\theta}\frac{\partial}{\partial \theta}\left(\sin\theta\frac{\partial Y_{L,M}}{\partial\theta}\right)+ \frac{1}{\sin^2\theta}\frac{\partial^2 Y_{L,M}}{\partial\phi^2}= - L(L+1) Y_{L,M}.\]
we can see that the wave functions are the spherical harmonics and the energies are given by
\[E_{L,M} = V_0 +\frac{L(L+1)\hbar^2}{2mR^2}\]
Note that the energies depend on \(L\) but not on the \(M\) quantum number. So, each state belonging to level \(L\) is \(2L+1\) fold degenerate because \(M\) ranges from \(-L\) to \(L\).
Finally, if instead of being constrained to move within a circle of radius R, the particle were constrained to move on the surface of the circle, the two-dimensional Schrödinger equation treated earlier would reduce to
\[- \frac{\hbar^2}{2mR^2} \frac{\partial^2\psi(\theta)}{\partial q^2} + V_0 \psi(\theta) = E\psi(\theta).\]
The solutions are the familiar functions
\[\psi(\theta) = \sqrt{(1/2 \pi)} \exp(in\theta)\]
with \(n = 0, ±1, ±2, …\)
and the energies are
\[E_n = \frac{n^2 \hbar^2}{2mR^2} + V_0.\]
Note that the quantization of energy arises because the angular momentum is quantized to be \(nh\); this condition arose, in turn, by the condition that
\[\psi(\theta) = \psi(q +2\pi).\]
As with the case of a particle moving within the circular region, the states with \(n > 0\) are doubly degenerate; the difference between pairs of such states reflecting the sense of their angular momentum.
These model problems will be seen in Chapter 2 to be very useful representations of situations that arise when an electron is constrained within or on the surface of various nanoscopic particles. For now, they were discussed to illustrate how separations of variables can sometimes be used to decompose the Schrödinger equation into one-dimensional ordinary differential equations and to show how it is the boundary conditions (either constraining \(y\) to vanish at certain distances or insisting that \(y\) be periodic when appropriate) that produce the quantization. It is important to note that it is when a particle is spatially constrained (e.g., when its wave function was forced to vanish at two locations \(x = 0\) and \(x = L_x\)) that quantized energy levels result. When the particle is not so spatially trapped, its energy will not be quantized. You will see this behavior over and over as we explore other models for electronic, vibrational, and rotational motions in molecules.
Quantized Action Can Also be Used to Derive Energy Levels
There is another approach that can be used to find energy levels and is especially straightforward to use for systems whose Schrödinger equations are separable. The so-called classical action (denoted \(S\)) of a particle moving with momentum p along a path leading from initial coordinate \(q_i\) at initial time \(t_i\) to a final coordinate \(q_f\) at time \(t_f\) is defined by:
\[S = \int_{\textbf{q}_i;t_i}^{\textbf{q}_f;t_f}\textbf{p}\cdot\textbf{dq} .\]
Here, the momentum vector p contains the momenta along all coordinates of the system, and the coordinate vector \(q\) likewise contains the coordinates along all such degrees of freedom. For example, in the two-dimensional particle-in-a-box problem considered above, \(\textbf{q} = (x, y)\) has two components as does \(\textbf{p} = (p_x, p_y)\), and the action integral is:
\[ S =\int_{x_i;y_i;t_i}^{x_f;y_f;t_f}(p_xdx+p_ydy).\]
In computing such actions, it is essential to keep in mind the sign of the momentum as the particle moves from its initial to its final positions. The examples given below will help clarify these matters and will show how to apply the idea.
For systems for which the Hamiltonian is separable, the action integral decomposes into a sum of such integrals, one for each degree of freedom. In the two-dimensional example, the additivity of H:
\[ H = H_x + H_y = \frac{p_x^2}{2m} + \frac{p_y^2}{2m} + V(x) + V(y)\]
\[ = - \frac{\hbar^2}{2m} \frac{\partial^2}{\partial x^2} + V(x) - \frac{\hbar^2}{2m} \frac{\partial^2}{\partial y^2} + V(y)\]
means that \(p_x\) and \(p_y\) can be independently solved for in terms of the potentials \(V(x)\) and \(V(y)\) as well as the energies \(E_x\) and \(E_y\) associated with each separate degree of freedom:
\[p_x = \pm\sqrt{2m(E_x-V(x))}\]
\[p_y = \pm\sqrt{2m(E_y-V(y))} ;\]
the signs on \(p_x\) and \(p_y\) must be chosen to properly reflect the motion that the particle is actually undergoing at any instant of time. Substituting these expressions into the action integral yields:
\[ S = S_x + S_y\]
\[= \int_{x_i;t_i}^{x_f;t_f} \pm\sqrt{2m(E_x-V(x))} dx + \int_{y_i;t_i}^{y_f;t_f} \pm\sqrt{2m(E_y-V(y))} dy.\]
The relationship between these classical action integrals and the existence of quantized energy levels has been shown to involve equating the classical action for motion that is periodic between a left and right turning point, as for a classical particle undergoing periodic vibrational motion, to the following multiple of Planck's constant:
\[S_{\text{closed}} = \int_{q_i;t_i}^{q_f;t_f} qdq= (n +\frac{1}{2}) h,\]
where the quantization index \(n\) ranges from 0 to \(\infty\) in steps of unity. Alternatively, for motion in a closed angular path, as for a particle moving on a circular or elliptical path, the action quantization condition reads:
\[S_{\text{closed}} =\int_{q_i;t_i}^{q_f;t_f} pdq = nh,\]
where again \(n\) ranges from 0 to \(\infty\) in steps of unity.
When action-quantization as described above is applied to the so-called harmonic oscillator problem (this serves as the simplest reasonable model for vibration of a diatomic molecule AB) that we will study in quantum form later, one expresses the total energy as the sum of kinetic and potential energies
\[E = \frac{p^2}{2m} + \frac{k}{2} x^2\]
where \[m = \dfrac{m_Am_B}{m_A + m_B}\] is the reduced mass of the AB diatomic molecule, \(k\) is the force constant describing the bond between A and B, \(x\) is the bond-length displacement, and p is the momentum associated with the bond length. The quantized action requirement then reads
\[(n +\frac{1}{2}) h = \int p dx = \int \sqrt{2\mu(E-k/2 x^2)} dx.\]
This integral is carried out between \(x = - \sqrt{2E/k}\) and \(\sqrt{2E/k}\) the left and right turning points of the oscillatory motion and back again to form a closed path. Carrying out this integral and equating it to \((n +\frac{1}{2}) h\) gives the following expression for the energy \(E\):
\[E = (n +\frac{1}{2}) (\hbar^2\pi) \sqrt{\dfrac{k}{\mu}} .\]
If the quantum number \(n\) is allowed to assume integer values ranging from \(n = 0\), 1, 2, to infinity, these energy levels agree with the full quantum treatment’s results that we will obtain later.
For an example of applying this approach to a problem involving motion along a closed loop, let’s consider the free (i.e., with no potential affecting its angular motion) rotation of a diatomic molecule AB having fixed bond length R. The rotational energy can be written as
\[E=\frac{p_\phi^2}{2\mu R^2}\]
where is the momentum associated with rotation and \(m\) is the reduced mass of the AB molecule. Solving for and inserting this into the action-quantization equation appropriate for motion along a closed loop gives
\[\int_{\phi=0}^{\phi=2\pi} p_\phi d\phi=\int_{\phi=0}^{\phi=2\pi} \sqrt{2\mu R^2E} d\phi = \sqrt{2\mu R^2 E}(2\pi) = nh.\]
Solving for the energy \(E\) then gives
\[E=\frac{(nh)^2}{(2\pi)^22\mu R^2}=\frac{n^2h^2}{2\mu R^2},\]
which is exactly the same result as we obtained earlier when solving the Schrödinger equation for the motion of a particle moving on a circle.
Now, let’s apply action quantization to each of the independent coordinates of the two-dimensional particle in a box problem. The two separate action quantization conditions read:
\[\big(n_x +\dfrac{1}{2}\big) h =\int_{x=0}^{x=L_x} \sqrt{2m(E_x-V(x))} dx +\int_{x=L_x}^{x=0} -\sqrt{2m(E_x-V(x))} dx \]
\[ (n_y +\dfrac{1}{2}) h = \int_{y=0}^{y=L_y} \sqrt{2m(E_y-V(y))} dy +\int_{y=L_y}^{y=0} -\sqrt{2m(E_y-V(y))} dy .\]
Notice that the sign of the momenta are positive in each of the first integrals appearing above (because the particle is moving from \(x = 0\) to \(x = L_x\), and analogously for \(y\)-motion, and thus has positive momentum) and negative in each of the second integrals (because the motion is from \(x = L_x\) to \(x = 0\) (and analogously for \(y\)-motion) and thus the particle has negative momentum). Within the region bounded by \(0 \le x\le L_x; 0 \le y\le L_y\), the potential is constant and can be taken as zero (this just gives our reference point for total energy). Using this fact, and reversing the upper and lower limits, and thus the sign, in the second integrals above, one obtains:
\[\big(n_x +\dfrac{1}{2}\big) h = 2\int_{x=0}^{x=L_x} \sqrt{2mE_x} dx= 2\sqrt{2mE_x} L_x\]
\[\big(n_y +\dfrac{1}{2}\big) h = 2\int_{y=0}^{y=L_y} \sqrt{2mE_y} dy= 2\sqrt{2mE_y} L_y.\]
Solving for \(E_x\) and \(E_y\), one finds:
\[E_x =\frac{[\big(n_x +\dfrac{1}{2}\big)h]^2}{8mL_x^2}\]
\[E_y =\frac{[\big(n_y +\dfrac{1}{2}\big)h]^2}{8mL_y^2} .\]
These are not the same quantized energy levels that arose when the wave function boundary conditions were matched at \(x = 0\), \(x = L_x\) and \(y = 0\), \(y = L_y\). In the Schrödinger equation approach, the energy expressions did not have the + \(\dfrac{1}{2}\) factor that appears in the above action-based result. It turns out that, for potentials that are defined in a piecewise manner, as the particle-in-a-box potential is (i.e., the potential undergoes an infinite jump at \(x = 0\) and \(x = L\)), the action quantization condition has to be modified. An example of how and why one has to make this modification is given in a paper from Prof. Bill Miller’s group (J. E. Adams and W. H. Miller, J. Chem. Phys. 67, 5775-5778 (1977)), but I will not discuss it further here because its details are beyond the level of this text. Suffice it to say that for periodic motion between two turning points on a smooth (i.e., non-piecewise) potential, \((n+\dfrac{1}{2})h\) is the correct action quantization value. For angular motion on a closed loop, nh is the proper value. But, for periodic motion between turning points on a piecewise potential, the modifications discussed in the above reference must be applied to cause action quantization to reproduce the correct quantum result.
The use of action quantization as illustrated above has become a very important tool. It has allowed scientists to make great progress toward bridging the gap between classical and quantum descriptions of molecular dynamics. In particular, by using classical concepts such as trajectories and then imposing quantized-action conditions, people have been able to develop so-called semi-classical models of molecular dynamics. In such models, one is able to retain a great deal of classical understanding while building in quantum effects such as energy quantization, zero-point energies, and interferences. Both at my Theory Page web site and from papers accessed on the web site of Professor William H. Miller, one of the pioneers of semi-classical theory as applied to chemistry, you can learn more about this subject.
Before leaving this section, it is worth discussing a bit more the energy and angular momentum quantization that occurs when treating free one-dimensional rotational motion of a particle on a circle or a linear rigid molecule constrained to lie on a plane. When we used action quantization to address this kind of problem, we obtained quantized energies
\[E=\frac{n^2h^2}{2\mu R^2}\]
which, through the energy expression given in terms of angular momentum
\[E=\frac{p_\phi^2}{2\mu R^2},\]
implies that the angular momentum itself is quantized
\[p_\phi=\pm nh.\]
This is the same result we obtain when we seek eigenfunctions and eigenvalues the quantum mechanics \(\textbf{L}_z\) angular momentum operator. As we showed earlier, this operator, when computed as the \(z\)-component of \(\textbf{R} \times \textbf{p}\), can be written in polar \((r, \theta, \phi)\) coordinates as
\[L_z = - i \hbar \dfrac{d}{d\phi}.\]
The eigenfunctions of this operator have the form \(\exp(ia\phi)\), and the eigenvalues are a h. Because geometries with azimuthal angles equal to \(\phi\) or equal to \(\phi + 2\pi\) are exactly the same geometries, the function \(\exp(ia\phi)\) should be exactly the same as \(\exp(ia(\phi+2\pi))\). This can only be the case if a is an integer. Thus, one concludes that only integral multiples of h can be allowed values of the \(z\)-component of angular momentum.
Experimentally, one measures the \(z\)-component of an angular momentum by placing the system possessing the angular momentum in a magnetic field of strength B and observing how many \(z\)-component energy states arise. This splitting in energy levels is termed the Zeeman effect. For example, a boron atom with one unpaired electron its \(2\pi\) orbital has one unit of orbital angular momentum, so one finds three separate \(z\)-component values which are usually denoted \(m = -1, m=0,\) and \(m=1\). Another example is offered by the scandium atom with one unpaired electron in a d orbital; this atom’s states split into five (\(m = -2, -1, 0, 1, 2\)) \(z\)-component states. In each case, one finds \(2L + 1\) values of the \(m\) quantum number, and, because L is an integer, \(2L + 1\) is an odd integer. Both of these observations are consistent with the expectation that only integer values can occur for \(L_z\) eigenvalues as obtained from action quantization and from the boundary condition \(\exp(ia\phi) = \exp(ia(\phi+2\pi))\).
However, it has been observed that some species do not possess 3 or 5 or 7 or 9 \(z\)-component states but an even number of such states. In particular, electrons, protons, or neutrons are observed to have only two \(z\)-component eigenvalues. This also is observed in, for example, the Boron atom mentioned above, if one examines the further splittings of the \(2\pi\) (m = -1, 0, and 1) levels caused by the magnetic field’s action on the unpaired electron’s spin. Because, as we discuss later in this text, all angular momenta have \(z\)-component eigenvalues that are separated from one another by unit multiples of h, one is forced to conclude that these three fundamental building-block particles (electrons, protons, and neutrons) have \(z\)-component eigenvalues of \(\dfrac{1}{2} \hbar\) and \(-\dfrac{1}{2} \hbar\). The appearance of half-integral angular momenta is not consistent with the action-quantization result or the observation made earlier that \(\phi\) and \(\phi + 2\pi\) correspond to exactly the same physical point in coordinate space, which, in turn, implies that only full-integer angular momenta are possible.
The resolution of the above paradox (i.e., how can half-integer angular momenta exist?) involves realizing that some angular momenta correspond not to the \(\textbf{R} \times \textbf{p}\) angular momenta of a physical mass rotating, but, instead, are intrinsic properties of certain particles. That is, the intrinsic angular momenta of electrons, protons, and neutrons can not be viewed as arising from rotation of some mass that comprises these particles. Instead, such intrinsic angular momenta are fundamental built in characteristics of these particles. For example, the two \(\dfrac{1}{2} \hbar\) and \(-\dfrac{1}{2} \hbar\) angular momentum states of an electron, usually denoted a and b, respectively, are two internal states of the electron that are degenerate in the absence of a magnetic field but which represent two distinct states of the electron. Analogously, a proton has \(\dfrac{1}{2} \hbar\) and \(-\dfrac{1}{2} \hbar\) states, as do neutrons. All such half-integral angular momentum states cannot be accounted for using classical mechanics but are known to arise in quantum mechanics. This means that, when we teach introductory chemistry to young students, it is not correct to say that the up and down (a and b) spin states of an electron can be viewed in terms of the electron’s mass spinning clockwise or counterclockwise around some axis. Such spinning-mass angular momenta can only possess integer values; half-integer angular momenta cannot and should not be described in terms of spinning masses.
Action Can Also be Used to Generate Wave Functions
Action integrals computed from classical descriptions of motion on potential energy surfaces can also be used to generate approximate quantum wave functions. So doing offers yet another avenue for making connection between the classical and quantum worlds. To see how such a connection can arise directly from the Schrödinger equation, we begin with the time-independent Schrödinger equation for a single particle of mass \(m\) moving on a potential \(V(r)\) that depends on the particle’s position coordinates \(r\):
\[E\Psi(r)=-\frac{\hbar^2}{2m}\nabla^2\Psi(r)+V(r)\Psi(r).\]
Then, we express the complex wave function as a constant real amplitude A multiplied by a complex phase which we write as:
\[\Psi(r)=A\exp(iW(r)/\hbar).\]
Substituting this expression for into the Schrödinger equation gives an equation for \(W\):
\[E=V+\frac{(\nabla W)^2}{2m}-i\hbar\frac{\nabla^2W}{2m}.\]
This equation contains both real and imaginary components (n.b., \(W\) itself is complex). It is usually solved by assuming \(W(r)\) can be expanded in a power series in the variable \(\hbar\). This expansion is motivated by noting that if the \(\dfrac{\nabla^2 W}{2m}i\hbar\) factor in the above equation is neglected, the resulting equation
\[0=V-E+\frac{(\nabla W)^2}{2m}\]
would make sense if \(\nabla W(r)\) were equal to the classical momentum of the particle. So, taking the \(\hbar\rightarrow 0\) limit of the equation for \(W(r)\) appears to reduce this quantum mechanics equation to a classical result in which \(\nabla W(r) = p(r)\).
So, substituting
\[W(r)=W_0(r)+hW_1(r)+\hbar^2W_2(r)+\cdots\]
into the above equation for \(W(r)\) and gathering together all terms of a given power in produces equations for the various \(W_n(r)\), the first two of which read:
\[0=2m(V-E)+(\nabla W_0)^2\]
and
\[0=2\nabla W_0\cdot \nabla W_1-i\nabla^2 W_0.\]
To simplify further discussion of this so-called semi-classical wave function theory, let us restrict attention to the case in which there is only one spatial coordinate. For the two- or three-dimensional cases, \(\nabla W_0\) and \(\nabla W_1\) are vector quantities, and the solution of these equations is considerably more complicated, especially if the potential \(V(\textbf{r})\) can not be separated into additive contributions from each of the variables. When there is only one spatial coordinate, and are scalar quantities.
The first equation can be solved for \(W_0(r)\) and gives two independent solutions (i.e., those corresponding to the ± sign):
\[W_0(r)=\pm\int\sqrt{2m(E-V(r^\prime))dr^\prime},\]
each of which will be real when \(E > V(r)\) (i.e., in classically allowed regions of space) and imaginary when \(E < V(r)\) (i.e., in classically forbidden regions). Notice that \(W_0(r)\) contains an integrand equal to the classical momentum \(p(r)=\sqrt{2m(E-V(r)) }\).
The equation for \(W_1(r)\) can also be solved:
\[W_1(r)=\frac{i}{2}\ln[\sqrt{2m(E-V(r))}].\]
So, through first-order in \(\hbar\), the semi-classical wave functions are
\[\Psi(r)=A\exp\left(\pm\frac{i}{\hbar}\int^r\sqrt{2m(E-V(r^\prime))}dr^\prime\right)\exp\left(\frac{i\hbar}{2h}i\ln[\sqrt{2m(E-V(r))}]\right).\]
\[=\frac{1}{\sqrt{\sqrt{2m(E-V(r))}}}A\exp\left(\pm\frac{i}{\hbar}\int^r\sqrt{2m(E-V(r^\prime))}dr^\prime\right)\]
These pairs of wave functions are often expressed as
\[\Psi=\frac{1}{\sqrt{\sqrt{2m(E-V(r))}}}A\exp\left(\pm\frac{i}{\hbar}\int^r\sqrt{2m(E-V(r^\prime))}dr^\prime\right)\]
in regions of space where \(E > V\), and
\[\Psi=\frac{1}{\sqrt{\sqrt{2m(-E+V(r))}}}A\exp\left(\pm\frac{i}{\hbar}\int^r\sqrt{2m(-E+V(r^\prime))}dr^\prime\right)\]
in the classically forbidden regions where \(V > E\). Notice that the wave functions in the classically allowed regions have probability densities given by
\[\Psi^*\Psi=\frac{A^2}{\sqrt{2m(E-V(r))}}\]
which is exactly the classical probability density we discussed earlier in this Chapter. The probability is inversely proportional to the speed of the particle at location r, and has the same singularity as the classical probability at turning points (where \(V = E\)). In contrast, the probability densities in regions where \(V > E\) either grow or decay exponentially within these classically forbidden regions.
Let’s see how these semi-classical wave functions can be applied to some of the model problems we discussed earlier. For the one dimensional particle-in-a-box problem, the two exponentially growing and decaying functions are not needed because in the regions \(R < 0\) and \(R > L\), the wave function can be taken to vanish. Within the region \(0 \le r \le L\), there are two independent wave functions
\[\Psi=\frac{1}{\sqrt{\sqrt{2m(E-V(r))}}}A\exp\left(\pm\frac{i}{\hbar}\int^r\sqrt{2m(E-V(r^\prime))}dr^\prime\right),\]
and the potential \(V(r’)\) is constant (let’s call the potential in this region \(V_0\)). So, the integration appearing in these two wave functions can be carried out to give
\[\Psi=\frac{1}{\sqrt{\sqrt{2m(E-V(r))}}}A\exp\left(\pm\frac{ir}{\hbar}\sqrt{2m(E-V_0)}\right).\]
We can combine these two functions to generate a function that will vanish at \(R = 0\) (as it must for this particle-in-a-box problem):
\[\Psi=\frac{1}{\sqrt{\sqrt{2m(E-V(r))}}}A\left[\exp\left(\frac{ir}{\hbar}\sqrt{2m(E-V_0)}\right)-\exp\left(-\frac{ir}{\hbar}\sqrt{2m(E-V_0)}\right)\right].\]
We can then use the condition that \(\Psi\) must also vanish at \(R = L\) to obtain an equation that specifies the energies \(E\) that are allowed:
\[0=\left[\exp\left(\frac{iL}{\hbar}\sqrt{2m(E-V_0)}\right)-\exp\left(-\frac{iL}{\hbar}\sqrt{2m(E-V_0)}\right)\right]=2i\sin\left(\frac{L}{\hbar}\sqrt{2m(E-V_0)}\right),\]
which means that
\[E=V_0+\frac{n^2\pi^2\hbar^2}{2mL^2}.\]
These energies are exactly the same as we found when we solved the Schrödinger equation for this model problem.
It is informative to note that these semi-classical wave functions, which are not exact because they were obtained by retaining only terms up to the first power of \(\hbar\), were able to generate quantum nodal patterns (i.e., interferences) and quantized energy levels even though they contained classical concepts such as the momentum at various positions in space. It was by superimposing two functions having the same energy that nodal patterns were obtained.
Let’s now consider what happens when we apply the semi-classical wave function to the harmonic oscillator problem also discussed earlier. In this case, there are two classical turning points \(r_1\) and \(r_2\) at which \(E = V(r)\). The semi-classical wave functions appropriate to the three regions (two classically forbidden and one classically allowed) are:
\[\Psi_1=\frac{1}{\sqrt{\sqrt{2m(-E+V(r))}}}A_1\exp\left(-\frac{1}{\hbar}\int_{r_2}^r\sqrt{2m(-E+V(r^\prime))}dr^\prime\right),r\ge r_2.\]
\[\Psi_2=\frac{1}{\sqrt{\sqrt{2m(-E+V(r))}}}A_2\exp\left(\frac{1}{\hbar}\int_{r_1}^r\sqrt{2m(-E+V(r^\prime))}dr^\prime\right),r\le r_1.\]
\[\Psi_3=\frac{1}{\sqrt{\sqrt{2m(E-V(r))}}}\left[A_3\exp\left(\frac{i}{\hbar}\int_{r_1}^r\sqrt{2m(E-V(r^\prime))}dr^\prime\right)-A_{3^\prime}\exp\left(-\frac{i}{\hbar}\int_{r}^{r_2}\sqrt{2m(E-V(r^\prime))}dr^\prime\right)\right],r_1\le r\le r_2.\]
The first two decay exponentially within the two classically forbidden regions. The third is a combination of the two independent solutions within the classically allowed region, with the amplitudes of the two solutions defined by the coefficients \(A_3\) and \(A_{3’}\). The amplitudes \(A_1\) and \(A_2\) multiply the wave functions in the two classically forbidden regions, and all four amplitudes as well as the energy \(E\) must be determined by (i) normalizing the total wave function to obey
\[\int_{-\infty}^{\infty}\Psi^*\Psi dr=1\]
and (2) by matching the wave functions \(\Psi_1\) and \(\Psi_3\) and their first derivatives at \(R = r_1\), and the wave functions \(\Psi_2\) and \(\Psi_3\) and their first derivatives at \(R = r_2\).
Before addressing how this wave function matching might be accomplished, let me point out an interesting property of the factor entering into the exponential of the semi-classical wave function. We first use the two expressions
\[\frac{dW_0}{dr}=\pm\sqrt{2m(E-V(r))} \]
and
\[\frac{dW_1}{dr}=\dfrac{i\dfrac{d\sqrt{2m(E-V)}}{dr}}{2\sqrt{2m(E-V)}}\]
given above for the first two components of \(W(r)\) and then make use of the harmonic form of \(V(r)\)
\[V(r)=\frac{1}{2}kr^2.\]
Next, we evaluate the integral of \(\dfrac{dW}{dr}\) for a closed classical path in which the system moves from the left turning point
\[r_1=-\sqrt{\frac{2E}{k}}\]
to the right turning point
\[r_2=\sqrt{\frac{2E}{k}}\]
and back again to the left turning point. The contribution from integrating \(\dfrac{dW_0}{dr}\) along this closed path is (n.b., the + sign is used for the first part of the path because the particle has positive momentum, and the – sign applies to the return part of the path when the particle has negative momentum):
\[W_0=\int_{r_1}^{r_2}\sqrt{2m\Big(E-\frac{1}{2}kr^2\Big)}dr-\int_{r_2}^{r_1}\sqrt{2m\Big(E-\frac{1}{2}kr^2\Big)}dr\]
which is exactly the action integral we treated earlier in this Chapter when we computed for the classical harmonic oscillator. The contribution from integrating \(\dfrac{dW_1}{dr}\) along this closed path can be evaluated by first writing
\[\frac{dW_1}{dr}=\dfrac{i\dfrac{d\sqrt{2m(E-1/2 kr^2)}}{dr}}{2\sqrt{2m(E-1/2 kr^2)}}=\frac{-ikr}{4(E-1/2 kr^2)}.\]
The integral from \(r_1\) to \(r_2\) of this quantity can be carried out (using the substitution \(r = \sqrt{2E/k} y\)) as
\[\dfrac{-ik}{4}\int_{-\sqrt{2E/k}}^{\sqrt{2E/k}}\dfrac{rdr}{(E-1/2kr^2)}=\dfrac{-ik}{4}\int_{-1}^{1}\dfrac{\dfrac{2E}{k}ydy}{E(1-y^2)}=\dfrac{-i}{4}\int_{-1}^{1}\dfrac{ydy}{(1-y)(1+y)}.\]
The evaluation of the integral remaining on the right-hand side can be done using contour integration (undergraduate students may not have encountered this subject within complex variable theory; I refer them to pp. 367-377 Methods of Theoretical Physics, P. M. Morse and H. Feshabach, McGraw-Hill, New York (1953) or p. 113 Applied Complex Variables, J. W. Dettman, Macmillan Co. New York (1965)). The basic equation from contour integration says that an integral of the form \(\int \dfrac{f(z)}{(z-a)}dz\), where \(z = a\) is a singularity, is equal to \(2\pi if(a)\). Our integral has singularities at \(y = 1\) and at \(y = -1\), so there are two such contributions. The net result is that our integral reduces to
\[\frac{-i}{4}\int_{-1}^{1}\frac{ydy}{(1-y)(1+y)}=\frac{i}{4}2\pi i\left[\frac{1}{2}+\frac{-1}{-2}\right]=-\frac{\pi}{2}.\]
So, the contribution to the integral of \(\dfrac{dW_1}{dr}\) arising from \(r_1\) to \(r_2\) is equal to \(–\pi/2\). The integral from \(r_2\) back to \(r_1\) gives another factor or \(–\dfrac{\pi}{2}\). Combining the integral of \(\dfrac{dW_0}{dr}\) and the integral of \(\dfrac{dW_1}{dr}\) (multiplied by because \(W = W_0 + \hbar W_1 + …\)) gives the following final result
\[W=\int_{r_1}^{r_2}\sqrt{2m\Big(E-\frac{1}{2}kr^2\Big)}dr-\int_{r_2}^{r_1}\sqrt{2m\Big(E-\frac{1}{2}kr^2\Big)}dr-\pi \hbar\]
If the original Bohr quantization is applied to the integral of \(\dfrac{dW}{dr}\) along a closed classical path:
\[W=nh,n=1,2,3,\cdots\]
our result above then says that
\[nh=\int_{r_1}^{r_2}\sqrt{2m\Big(E-\frac{1}{2}kr^2\Big)}dr-\int_{r_2}^{r_1}\sqrt{2m\Big(E-\frac{1}{2}kr^2\Big)}dr-\frac{1}{2}h\]
which is the same as
\[\int p(r)dr=\big(n+\dfrac{1}{2}\big)h.\]
This means that the \(\dfrac{1}{2}\) factor that arises in the action quantization condition for periodic motions between two turning points can be viewed as arising from the first quantum correction (i.e., the term first order in \(\hbar\)) to the semi-classical wave function. Recall that equating this classical action integral to \(\big(n+\dfrac{1}{2}\big) h\) gave the correct (i.e., quantum) energies for this harmonic oscillator problem.
We have seen how a semi-classical wave function can be defined, what its spatial probability density is, how it can build in interference (to achieve proper nodal patterns), and how quantizing its action can give the correct allowed energy levels. However, there is one issue we have not fully addressed. To solve for the coefficients \((A_1, … A_{3’})\) multiplying the semi-classical wave functions in the classically allowed and forbidden regions, the wave functions \(\Psi_1\) and \(\Psi_3\) and their first derivatives must be matched at \(r = r_1\), and the wave functions \(\Psi_2\) and \(\Psi_3\) and their first derivatives must be matched at \(R\) = \(r_2\). Unfortunately, the details of this matching process are rather complicated and require examining in more detail the nature of the wave functions near the classical turning points where each of \(\Psi_1\), \(\Psi_2\), and \(\Psi_3\) contain factors of the form \(\sqrt{\sqrt{2m(-E+V(r)}}\) in their denominators. It should be clear that matching functions and their derivatives that contain such singularities pose special challenges. I will not go further into this matter here; rather, I refer the interested reader to pp. 268-279 of Quantum Mechanics, 3rd Ed., L. I. Schiff, McGraw-Hill, New York (1968) for a good treatment of this so-called WKB approach to the matching issue.
Contributors and Attributions
Jack Simons (Henry Eyring Scientist and Professor of Chemistry, U. Utah) Telluride Schools on Theoretical Chemistry
Integrated by Tomoyuki Hayashi (UC Davis)


