14.5: The Chemical Shift Tells How Far the Signal Is from the Reference Signal
- Page ID
- 13937
5.3A: The basics of an NMR experiment
Given that chemically nonequivalent protons have different resonance frequencies in the same applied magnetic field, we can see how NMR spectroscopy can provide us with useful information about the structure of an organic molecule. A full explanation of how a modern NMR instrument functions is beyond the scope of this text, but in very simple terms, here is what happens. First, a sample compound (we'll use methyl acetate) is placed inside a very strong applied magnetic field (B0).

All of the protons begin to precess: the Ha protons at precessional frequency ωa, the Hb protons at ωb.At first, the magnetic moments of (slightly more than) half of the protons are aligned with B0, and half are aligned against B0. Then, the sample is hit with electromagnetic radiation in the radio frequency range. The two specific frequencies which match ωaandωb(i.e. the resonance frequencies) cause those Ha and Hb protons which are aligned with B0 to 'flip' so that they are now aligned against B0. In doing so, the protons absorb radiation at the two resonance frequencies. The NMR instrument records which frequencies were absorbed, as well as the intensity of each absorbance.
In most cases, a sample being analyzed by NMR is in solution. If we use a common laboratory solvent (diethyl ether, acetone, dichloromethane, ethanol, water, etc.) to dissolve our NMR sample, however, we run into a problem – there many more solvent protons in solution than there are sample protons, so the signals from the sample protons will be overwhelmed. To get around this problem, we use special NMR solvents in which all protons have been replaced by deuterium. Recall that deuterium is NMR-active, but its resonance frequency is very different from that of protons, and thus it is `invisible` in 1H-NMR. Some common NMR solvents are shown below.

5.3B: The chemical shift
Let's look at an actual 1H-NMR plot for methyl acetate. Just as in IR and UV-vis spectroscopy, the vertical axis corresponds to intensity of absorbance, the horizontal axis to frequency (typically the vertical axis is not shown in an NMR spectrum).
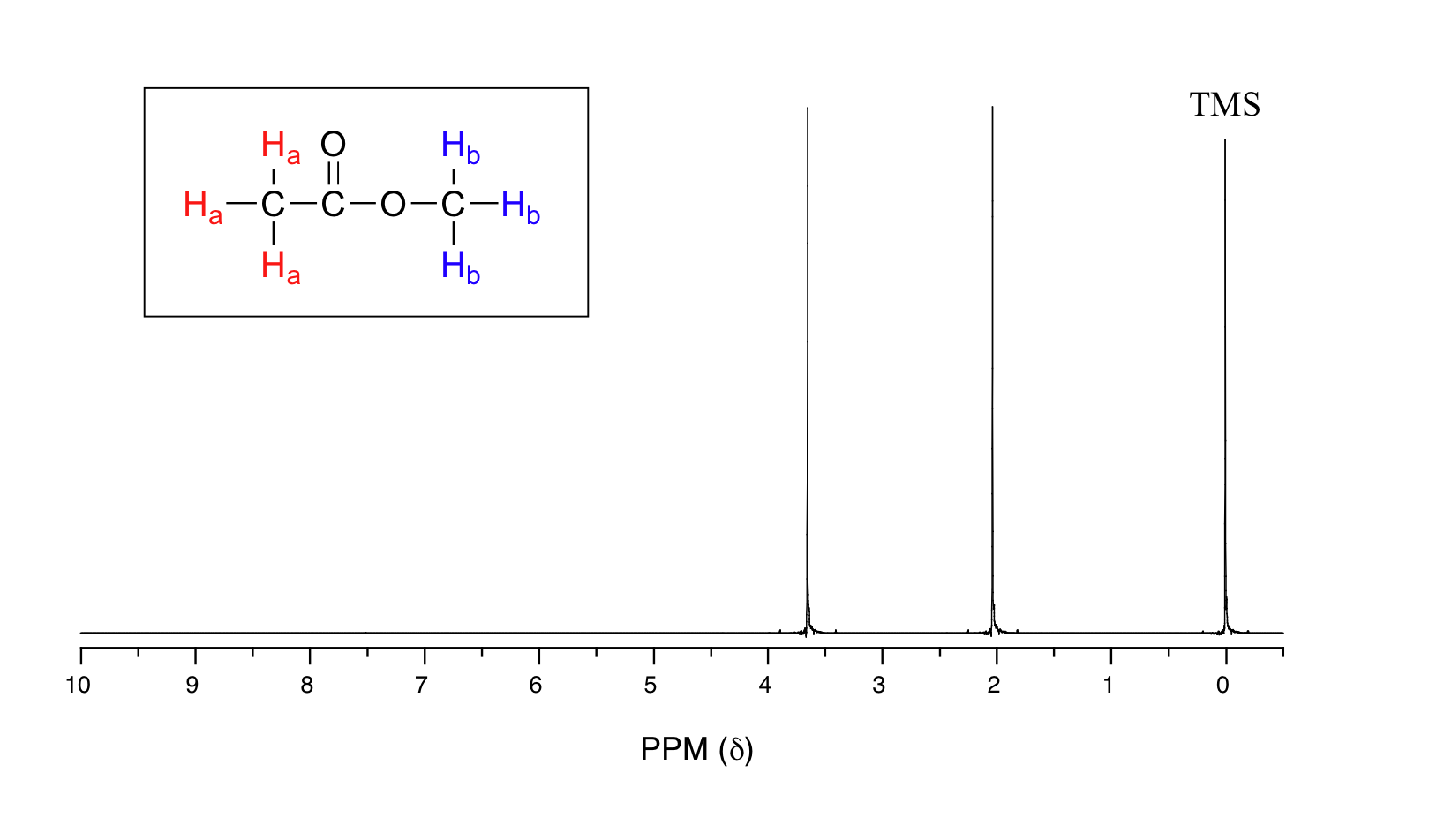
We see three absorbance signals: two of these correspond to Ha and Hb, while the peak at the far right of the spectrum corresponds to the 12 chemically equivalent protons in tetramethylsilane (TMS), a standard reference compound that was added to our sample.
You may be wondering about a few things at this point - why is TMS necessary, and what is the meaning of the `ppm (δ)` label on the horizontal axis? Shouldn't the frequency units be in Hz? Keep in mind that NMR instruments of many different applied field strengths are used in organic chemistry laboratories, and that the proton's resonance frequency range depends on the strength of the applied field. The spectrum above was generated on an instrument with an applied field of approximately 7.1 Tesla, at which strength protons resonate in the neighborhood of 300 million Hz (chemists refer to this as a 300 MHz instrument). If our colleague in another lab takes the NMR spectrum of the same molecule using an instrument with a 2.4 Tesla magnet, the protons will resonate at around 100 million Hz (so we’d call this a 100 MHz instrument). It would be inconvenient and confusing to always have to convert NMR data according to the field strength of the instrument used. Therefore, chemists report resonance frequencies not as absolute values in Hz, but rather as values relative to a common standard, generally the signal generated by the protons in TMS. This is where the ppm – parts per million – term comes in. Regardless of the magnetic field strength of the instrument being used, the resonance frequency of the 12 equivalent protons in TMS is defined as a zero point. The resonance frequencies of protons in the sample molecule are then reported in terms of how much higher they are, in ppm, relative to the TMS signal (almost all protons in organic molecules have a higher resonance frequency than those in TMS, for reasons we shall explore quite soon).
The two proton groups in our methyl acetate sample are recorded as resonating at frequencies 2.05 and 3.67 ppm higher than TMS. One-millionth (1.0 ppm) of 300 MHz is 300 Hz. Thus 2.05 ppm, on this instrument, corresponds to 615 Hz, and 3.67 ppm corresponds to 1101 Hz. If the TMS protons observed by our 7.1 Tesla instrument resonate at exactly 300,000,000 Hz, this means that the protons in our ethyl acetate samples are resonating at 300,000,615 and 300,001,101 Hz, respectively. Likewise, if the TMS protons in our colleague's 2.4 Tesla instrument resonate at exactly 100 MHz, the methyl acetate protons in her sample resonate at 100,000,205 and 100,000,367 Hz (on the 100 MHz instrument, 1.0 ppm corresponds to 100 Hz). The absolute frequency values in each case are not very useful – they will vary according to the instrument used – but the difference in resonance frequency from the TMS standard, expressed in parts per million, should be the same regardless of the instrument.
Expressed this way, the resonance frequency for a given proton in a molecule is called its chemical shift. A frequently used symbolic designation for chemical shift in ppm is the lower-case Greek letter delta (δ). Most protons in organic compounds have chemical shift values between 0 and 12 ppm from TMS, although values below zero and above 12 are occasionally observed. By convention, the left-hand side of an NMR spectrum (higher chemical shift) is called downfield, and the right-hand direction is called upfield.
In our methyl acetate example we included for illustrative purposes a small amount of TMS standard directly in the sample, as was the common procedure for determining the zero point with older NMR instruments.That practice is generally no longer necessary, as modern NMR instruments are designed to use the deuterium signal from the solvent as a standard reference point, then to extrapolate the 0 ppm baseline that corresponds to the TMS proton signal (in an applied field of 7.1 Tesla, the deuterium atom in CDCl3 resonates at 32 MHz, compared to 300 MHz for the protons in TMS). In the remaining NMR spectra that we will see in this text we will not see an actual TMS signal, but we can always assume that the 0 ppm point corresponds to where the TMS protons would resonate if they were present.
Example 5.2
A proton has a chemical shift (relative to TMS) of 4.56 ppm.
- What is its chemical shift, expressed in Hz, in a 300 MHz instrument? On a 200 MHz instrument?
- What is its resonance frequency, expressed in Hz, in a 300 MHz instrument? On a 200 MHz instrument?
(Assume that in these instruments, the TMS protons resonate at exactly 300 or 200 MHz, respectively)
5.3C: Signal integration
The computer in an NMR instrument can be instructed to automatically integrate the area under a signal or group of signals. This is very useful, because in 1H-NMR spectroscopy the area under a signal is proportional to the number of hydrogens to which the peak corresponds. The two signals in the methyl acetate spectrum, for example, integrate to approximately the same area, because they both correspond to a set of three equivalent protons.
Take a look next at the spectrum of para-xylene (IUPAC name 1,4-dimethylbenzene):
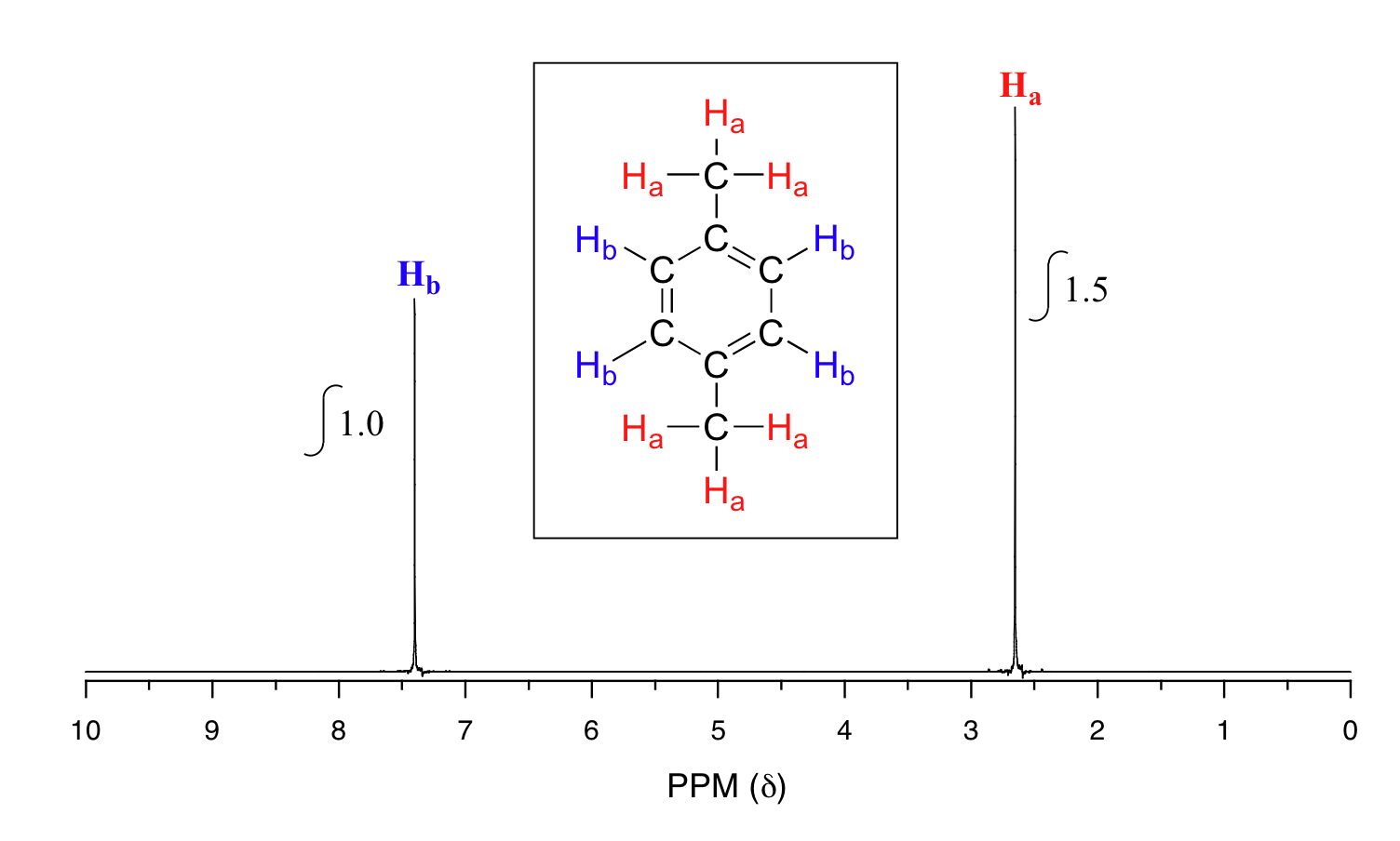
This molecule has two sets of protons: the six methyl (Ha) protons and the four aromatic (Hb) protons. When we instruct the instrument to integrate the areas under the two signals, we find that the area under the peak at 2.6 ppm is 1.5 times greater than the area under the peak at 7.4 ppm. This (along with the actual chemical shift values, which we'll discuss soon) tells us which set of protons corresponds to which NMR signal.
The integration function can also be used to determine the relative amounts of two or more compounds in a mixed sample. If we have a sample that is a 50:50 (mole/mole) mixture of benzene and acetone, for example, the acetone signal should integrate to the same value as the benzene sample, because both signals represent six equivalent protons. If we have a 50:50 mixture of acetone and cyclopentane, on the other hand, the ratio of the acetone peak area to the cylopentane peak area will be 3:5 (or 6:10), because the cyclopentane signal represents ten protons.
Example 5.3
You take a 1H-NMR spectrum of a mixed sample of acetone (CH3(CO)CH3) and dichloromethane (CH2Cl2). The integral ratio of the two signals (acetone : dichloromethane) is 2.3 to 1. What is the molar ratio of the two compounds in the sample?
Example 5.4
You take the 1H-NMR spectrum of a mixed sample of 36% para-xylene and 64% acetone in CDCl3 solvent (structures are shown earlier in this chapter). How many peaks do you expect to see? What is the expected ratio of integration values for these peaks? (set the acetone peak integration equal to 1.0)

