21.11: The pOH Concept
- Page ID
- 53940
Soap Lake has a long history as a healing place. Indian tribes would put aside their rivalries when they came to the lake to enjoy the high mineral content of the water. In the days before good antibiotics, thousands of visitors would come and enjoy the soothing waters of the lake. Soap Lake is alkaline, with water quality though to be similar to that of the moons of the planet Jupiter.
The pOH Concept
As with the hydrogen-ion concentration, the concentration of the hydroxide ion can be expressed logarithmically by the pOH. The pOH of a solution is the negative logarithm of the hydroxide-ion concentration:
\[\text{pOH} = -\text{log} \left[ \ce{OH^-} \right]\nonumber \]
The pH of a solution can be related to the pOH. Consider a solution with a pH \(= 4.0\). The \(\left[ \ce{H^+} \right]\) of the solution would be \(1.0 \times 10^{-4} \: \text{M}\). Dividing \(K_\text{w}\) by this yields a \(\left[ \ce{OH^-} \right]\) of \(1.0 \times 10^{-10} \: \text{M}\). Finally the pOH of the solution equals \(-\text{log} \left( 1.0 \times 10^{-10} \right) = 10\). This example illustrates the following relationship.
\[\text{pH} + \text{pOH} = 14\nonumber \]
The pOH scale is similar to the pH scale in that a pOH of 7 is indicative of a neutral solution. A basic solution has a pOH less than 7, while an acidic solution has a pOH of greater than 7. The pOH is convenient to use when finding the hydroxide ion concentration from a solution with a known pH.
Example \(\PageIndex{1}\)
Find the hydroxide concentration of a solution with a pH of 4.42.
Solution
Step 1: List the known values and plan the problem.
Known
- pH \(= 4.42\)
- pH \(+\) pOH \(= 14\)
Unknown
First, the pOH is calculated, followed by the \(\left[ \ce{OH^-} \right]\).
Step 2: Solve.
\[\begin{align*} \text{pOH} &= 14 - \text{pH} = 14 - 4.42 = 9.58 \\ \left[ \ce{OH^-} \right] &= 10^{-\text{pOH}} = 10^{-9.58} = 2.6 \times 10^{-10} \: \text{M} \end{align*}\nonumber \]
Step 3: Think about your result.
The pH is that of an acidic solution, and the resulting hydroxide-ion concentration is less than \(1 \times 10^{-7} \: \text{M}\). The answer has two significant figures because the given pH has two decimal places.
The diagram below shows all of the interrelationships between \(\left[ \ce{H^+} \right]\), \(\left[ \ce{OH^-} \right]\), pH, and pOH.
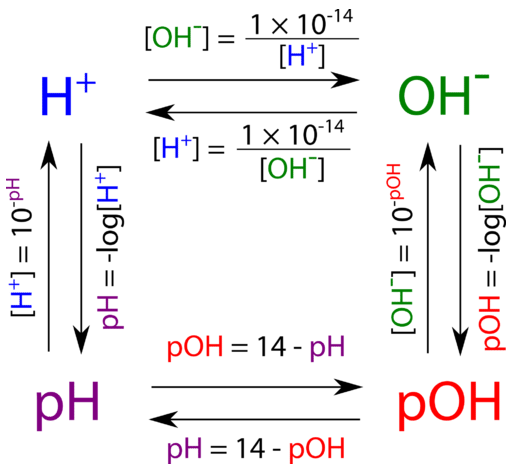
Summary
- The pOH of a solution is the negative logarithm of the hydroxide-ion concentration.
- Calculations involving pOH are described.

