18.9: Order of Reaction
- Page ID
- 53894
Forest fires cause extensive damage; both plant and animal life are harmed. The severity of a forest fire depends on how much plant life is available to burn—the more available dry plant material, the more serious the fire, and the more rapidly it will spread.
Order of Reaction
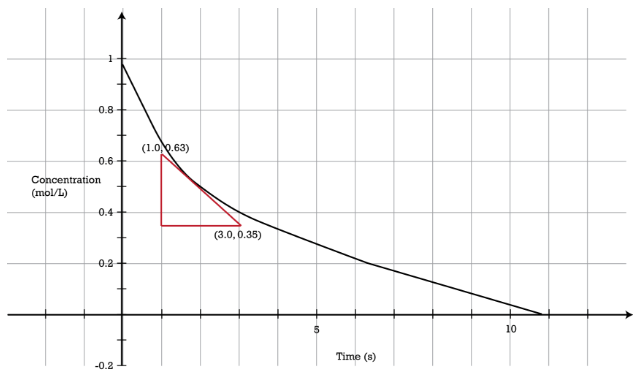
In the reaction \(\ce{A} \rightarrow \ce{B}\), the rate of the reaction is directly proportional to the concentration of \(\ce{A}\) raised to the first power. That is to say, \(\left[ \ce{A} \right] = \left[ \ce{A} \right]^1\). A first-order reaction is a reaction in which the rate is proportional to the concentration of only one reactant. As a first-order reaction proceeds, the rate of reaction decreases because the concentration of the reactant decreases (see figure below). The graph of concentration versus time is curved. The reaction rate \(\left( \frac{\Delta \left[ \ce{A} \right]}{\Delta t} \right)\) can be determined graphically by the slope of a tangent to the curve at any point. The rate of the reaction at the time shown with the red triangle is given by:
\[\text{rate} = -\frac{\left[ \ce{A} \right]_\text{final} - \left[ \ce{A} \right]_\text{initial}}{\Delta t} = -\frac{0.35 \: \text{M} - 0.63 \: \text{M}}{3.0 \: \text{s} - 1.0 \: \text{s}} = 0.14 \: \text{M/s}\nonumber \]
The rates of some reactions depend on the concentrations of more than one reactant. Consider a reaction in which a molecule of \(\ce{A}\) collides with a molecule of \(\ce{B}\) to form product \(\ce{C}\).
\[\ce{A} + \ce{B} \rightarrow \ce{C}\nonumber \]
Doubling the concentration of \(\ce{A}\) alone would double the reaction rate. Likewise, doubling the concentration of \(\ce{B}\) alone would also double the rate. The rate law must reflect the rate dependence on both reactants.
\[\text{rate} = k \left[ \ce{A} \right] \left[ \ce{B} \right]\nonumber \]
This reaction is said to be first order with respect to \(\ce{A}\) and first order with respect to \(\ce{B}\). Overall, it is a second-order reaction. The rate law and the order of a reaction must be determined experimentally.
Summary
- A first-order reaction is a reaction in which the rate is proportional to the concentration of only one reactant.
- As a first-order reaction proceeds, the rate of reaction decreases because the concentration of the reactant decreases (see figure below).

