2.6: Other Units - Temperature and Density
- Page ID
- 64014
- Learn about the various temperature scales that are commonly used in chemistry.
- Define density and use it as a conversion factor.
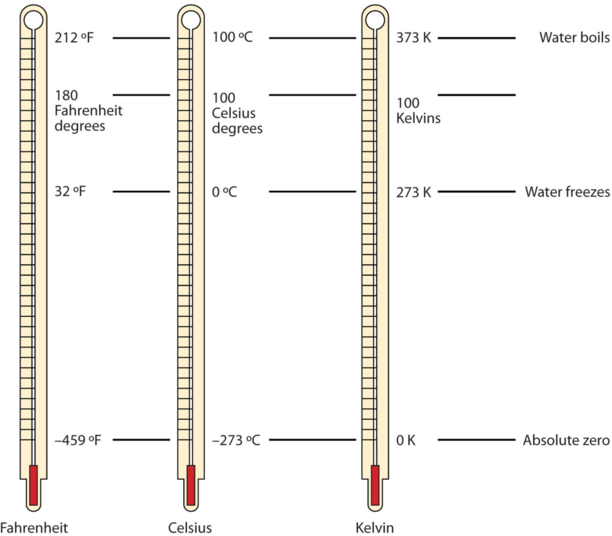
There are other units in chemistry that are important, and we will cover others over the course of the entire book. One of the fundamental quantities in science is temperature. Temperature is a measure of the average amount of energy of motion, or kinetic energy, a system contains. Temperatures are expressed using scales that use units called degrees, and there are several temperature scales in use. In the United States, the commonly used temperature scale is the Fahrenheit scale (symbolized by °F and spoken as "degrees Fahrenheit"). On this scale, the freezing point of liquid water (the temperature at which liquid water turns to solid ice) is 32°F, and the boiling point of water (the temperature at which liquid water turns to steam) is 212°F.
Science also uses other scales to express temperature. The Celsius scale (symbolized by °C and spoken as "degrees Celsius") is a temperature scale where 0°C is the freezing point of water and 100°C is the boiling point of water; the scale is divided into 100 divisions between these two landmarks and extended higher and lower. By comparing the Fahrenheit and Celsius scales, a conversion between the two scales can be determined:
\[\begin{align} \ce{^{\circ}C} &= \ce{(^{\circ}F-32)\times 5/9} \label{eq1} \\[4pt] \ce{ ^{\circ}F} &= \left(\ce{^{\circ}C \times 9/5 } \right)+32 \label{eq2} \end{align} \]
- What is 98.6 °F in degrees Celsius?
- What is 25.0 °C in degrees Fahrenheit?
Solution
- Using Equation \ref{eq1}, we have
\[\begin{align*} ^{\circ}C &=(98.6-32)\times \dfrac{5}{9} \\[4pt] &= 66.6\times \dfrac{5}{9} \\[4pt] &= 37.0^{\circ}C \end{align*}\nonumber \]
- Using Equation \ref{eq2}, we have
\[\begin{align*} ^{\circ}F &= \left(25.0\times \dfrac{9}{5}\right)+32 \\[4pt] &= 45.0+32 \\[4pt] &= 77.0^{\circ}F \end{align*}\nonumber \]
- Convert 0 °F to degrees Celsius.
- Convert 212 °C to degrees Fahrenheit.
- Answer a
-
−17.8 °C
- Answer b
-
414 °F
The fundamental unit of temperature (another fundamental unit of science, bringing us to four) in SI is the kelvin (K). The Kelvin temperature scale (note that the name of the scale capitalizes the word Kelvin, but the unit itself is lowercase) uses degrees that are the same size as the Celsius degree, but the numerical scale is shifted up by 273.15 units. That is, the conversion between the Kelvin and Celsius scales is as follows:
\[K = {^{\circ}C + 273.15}\nonumber \]
For most purposes, it is acceptable to use 273 instead of 273.15. Note that the Kelvin scale does not use the word degrees; a temperature of 295 K is spoken of as "two hundred ninety-five kelvins" and not "two hundred ninety-five degrees Kelvin."
The reason that the Kelvin scale is defined this way is because there exists a minimum possible temperature called absolute zero (zero kelvins). The Kelvin temperature scale is set so that 0 K is absolute zero, and temperature is counted upward from there. Normal room temperature is about 295 K, as seen in the following example.
If normal room temperature is 72.0°F, what is room temperature in degrees Celsius and kelvin?
Solution
First, we use the formula to determine the temperature in degrees Celsius:
\[\begin{align*} ^{\circ}C &= (72.0-32)\times \dfrac{5}{9} \nonumber \\[4pt] &= 40.0\times \dfrac{5}{9} \nonumber \\[4pt] &= 22.2^{\circ}C \end{align*}\nonumber \]
Then we use the appropriate formula above to determine the temperature in the Kelvin scale:
\[\begin{align*} K &= 22.2^{\circ}C+273.15 \nonumber \\[4pt] &= 295.4K \end{align*}\nonumber \]
So, room temperature is about 295 K.
What is 98.6°F on the Kelvin scale?
- Answer
-
310.2 K
Figure \(\PageIndex{1}\) compares the three temperature scales. Note that science uses the Celsius and Kelvin scales almost exclusively; virtually no practicing chemist expresses laboratory-measured temperatures with the Fahrenheit scale. In fact, the United States is one of the few countries in the world that still uses the Fahrenheit scale on a daily basis. The other two countries are Liberia and Myanmar (formerly Burma). People driving near the borders of Canada or Mexico may pick up local radio stations on the other side of the border that express the daily weather in degrees Celsius, so do not get confused by their weather reports.
Density
Density is a physical property that is defined as a substance's mass divided by its volume:
\[density= \dfrac{mass}{volume}\Rightarrow d= \dfrac{m}{v}\nonumber \]
Density is usually a measured property of a substance, so its numerical value affects the significant figures in a calculation. Notice that density is defined in terms of two dissimilar units, mass and volume. That means that density overall has derived units, just like velocity. Common units for density include g/mL, g/cm3, g/L, kg/L, and even kg/m3. Densities for some common substances are listed in Table \(\PageIndex{1}\).
| Substance | Density (g/mL or g/cm3) |
|---|---|
| water | 1.0 |
| gold | 19.3 |
| mercury | 13.6 |
| air | 0.0012 |
| cork | 0.22–0.26 |
| aluminum | 2.7 |
| iron | 7.87 |
Because of how it is defined, density can act as a conversion factor for switching between units of mass and volume. For example, suppose you have a sample of aluminum that has a volume of 7.88 cm3. How can you determine what mass of aluminum you have without measuring it? You can use the volume to calculate it. If you multiply the given volume by the known density (from Table \(\PageIndex{1}\)), the volume units will cancel and leave you with mass units, telling you the mass of the sample:
\[7.88\,\cancel{cm^{3}}\times \dfrac{2.7\,g}{\cancel{cm^{3}}}= 21\, g \text{ of aluminium} \nonumber \nonumber \]
where we have limited our answer to two significant figures.
What is the mass of 44.6 mL of mercury?
Solution
Use the density from Table \(\PageIndex{1}\) "Densities of Some Common Substances" as a conversion factor to go from volume to mass:
\[44.6\,\cancel{mL}\times \dfrac{13.6\,g}{\cancel{mL}}= 607\,g \nonumber \nonumber \]
The mass of the mercury is 607 g.
What is the mass of 25.0 cm3 of iron?
- Answer
-
197 g
Density can also be used as a conversion factor to convert mass to volume—but care must be taken. We have already demonstrated that the number that goes with density normally goes in the numerator when density is written as a fraction. Take the density of gold, for example:
\[d=19.3\,g/mL =\dfrac{19.3\,g}{mL} \nonumber \nonumber \]
Although this was not previously pointed out, it can be assumed that there is a 1 in the denominator:
\[d=19.3\,g/mL =\dfrac{19.3\,g}{mL} \nonumber \nonumber \]
That is, the density value tells us that we have 19.3 grams for every 1 milliliter of volume, and the 1 is an exact number. When we want to use density to convert from mass to volume, the numerator and denominator of density need to be switched—that is, we must take the reciprocal of the density. In so doing, we move not only the units, but also the numbers:
\[\dfrac{1}{d}= \dfrac{1\,mL}{19.3\,g} \nonumber \nonumber \]
This reciprocal density is still a useful conversion factor, but now the mass unit will cancel and the volume unit will be introduced. Thus, if we want to know the volume of 45.9 g of gold, we would set up the conversion as follows:
\[45.9\,\cancel{g}\times \dfrac{1\,mL}{19.3\cancel{g}}= 2.38\,mL \nonumber \nonumber \]
Note how the mass units cancel, leaving the volume unit, which is what we are looking for.
A cork stopper from a bottle of wine has a mass of 3.78 g. If the density of cork is 0.22 g/cm3, what is the volume of the cork?
Solution
To use density as a conversion factor, we need to take the reciprocal so that the mass unit of density is in the denominator. Taking the reciprocal, we find:
\[\dfrac{1}{d}= \dfrac{1\,cm^{3}}{0.22\,g} \nonumber \nonumber \]
We can use this expression as the conversion factor. So
\[3.78\,\cancel{g}\times \dfrac{1\,cm^{3}}{0.22\,\cancel{g}}= 17.2\,cm^{3} \nonumber \nonumber \]
What is the volume of 3.78 g of gold?
- Answer
-
0.196 cm3
Care must be used with density as a conversion factor. Make sure the mass units are the same, or the volume units are the same, before using density to convert to a different unit. Often, the unit of the given quantity must be first converted to the appropriate unit before applying density as a conversion factor.
Because degrees Fahrenheit is the common temperature scale in the United States, kitchen appliances, such as ovens, are calibrated in that scale. A cool oven may be only 150°F, while a cake may be baked at 350°F and a chicken roasted at 400°F. The broil setting on many ovens is 500°F, which is typically the highest temperature setting on a household oven.
People who live at high altitudes, typically 2,000 ft above sea level or higher, are sometimes urged to use slightly different cooking instructions on some products, such as cakes and bread, because water boils at a lower temperature the higher in altitude you go, meaning that foods cook slower. For example, in Cleveland water typically boils at 212°F (100°C), but in Denver, the Mile-High City, water boils at about 200°F (93.3°C), which can significantly lengthen cooking times. Good cooks need to be aware of this.

A meat thermometer with a dial. Notice the markings for Fahrenheit (outer scale) and Celsius (inner scale) temperatures. Recipes for cooking food in an oven can use very different numbers, depending on the country you're in. (CC BY2.0 Bev Sykes)
At the other end is pressure cooking. A pressure cooker is a closed vessel that allows steam to build up additional pressure, which increases the temperature at which water boils. A good pressure cooker can get to temperatures as high as 252°F (122°C); at these temperatures, food cooks much faster than it normally would. Great care must be used with pressure cookers because of the high pressure and high temperature. (When a pressure cooker is used to sterilize medical instruments, it is called an autoclave.)
Other countries use the Celsius scale for everyday purposes. Therefore, oven dials in their kitchens are marked in degrees Celsius. It can be confusing for US cooks to use ovens abroad—a 425°F oven in the United States is equivalent to a 220°C oven in other countries. These days, many oven thermometers are marked with both temperature scales.
Key Takeaways
- Chemistry uses the Celsius and Kelvin scales to express temperatures.
- A temperature on the Kelvin scale is the Celsius temperature plus 273.15.
- The minimum possible temperature is absolute zero and is assigned 0 K on the Kelvin scale.
- Density relates the mass and volume of a substance.
- Density can be used to calculate volume from a given mass or mass from a given volume.


