7.5: The First Law of Thermodynamics
- Page ID
- 24204
- To calculate changes in internal energy
To study the flow of energy during a chemical reaction, we need to distinguish between a system, the small, well-defined part of the universe in which we are interested (such as a chemical reaction), and its surroundings, the rest of the universe, including the container in which the reaction is carried out (Figure \(\PageIndex{1}\)). In the discussion that follows, the mixture of chemical substances that undergoes a reaction is always the system, and the flow of heat can be from the system to the surroundings or vice versa.
Three kinds of systems are important in chemistry. An open system can exchange both matter and energy with its surroundings. A pot of boiling water is an open system because a burner supplies energy in the form of heat, and matter in the form of water vapor is lost as the water boils. A closed system can exchange energy but not matter with its surroundings. The sealed pouch of a ready-made dinner that is dropped into a pot of boiling water is a closed system because thermal energy is transferred to the system from the boiling water but no matter is exchanged (unless the pouch leaks, in which case it is no longer a closed system). An isolated system exchanges neither energy nor matter with the surroundings. Energy is always exchanged between a system and its surroundings, although this process may take place very slowly. A truly isolated system does not actually exist. An insulated thermos containing hot coffee approximates an isolated system, but eventually the coffee cools as heat is transferred to the surroundings. In all cases, the amount of heat lost by a system is equal to the amount of heat gained by its surroundings and vice versa. That is, the total energy of a system plus its surroundings is constant, which must be true if energy is conserved.
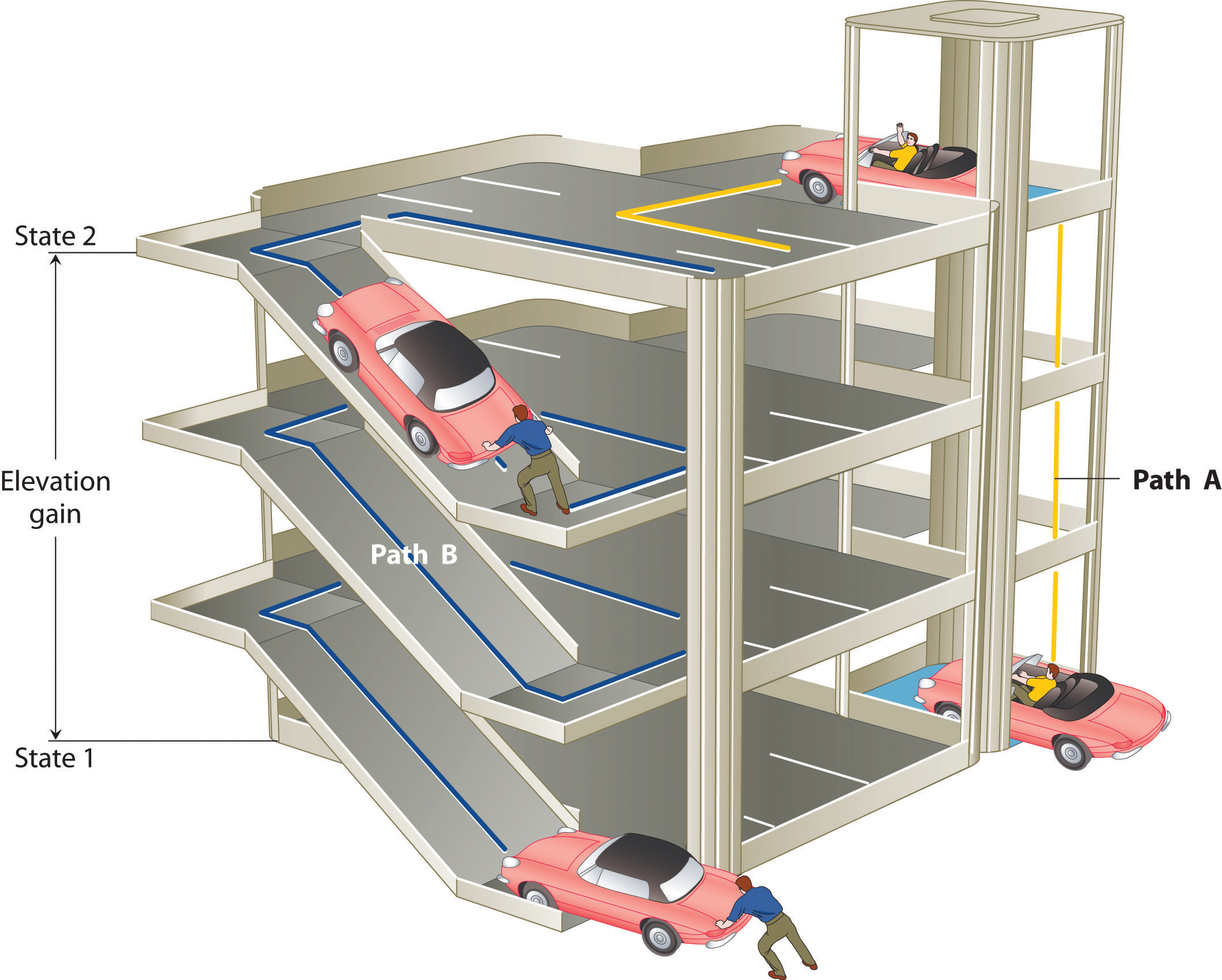
The state of a system is a complete description of a system at a given time, including its temperature and pressure, the amount of matter it contains, its chemical composition, and the physical state of the matter. A state function is a property of a system whose magnitude depends on only the present state of the system, not its previous history. Temperature, pressure, volume, and potential energy are all state functions. The temperature of an oven, for example, is independent of however many steps it may have taken for it to reach that temperature. Similarly, the pressure in a tire is independent of how often air is pumped into the tire for it to reach that pressure, as is the final volume of air in the tire. Heat and work, on the other hand, are not state functions because they are path dependent. For example, a car sitting on the top level of a parking garage has the same potential energy whether it was lifted by a crane, set there by a helicopter, driven up, or pushed up by a group of students (Figure \(\PageIndex{2}\)). The amount of work expended to get it there, however, can differ greatly depending on the path chosen. If the students decided to carry the car to the top of the ramp, they would perform a great deal more work than if they simply pushed the car up the ramp (unless, of course, they neglected to release the parking brake, in which case the work expended would increase substantially!). The potential energy of the car is the same, however, no matter which path they choose.
Direction of Heat Flow
The reaction of powdered aluminum with iron(III) oxide, known as the thermite reaction, generates an enormous amount of heat—enough, in fact, to melt steel (see chapter opening image).
The balanced chemical equation for the reaction is as follows:
\[ 2Al(s) + Fe_2O_3(s) \rightarrow 2Fe(s) + Al_2O_3(s) \tag{7.5.1}\]
We can also write this chemical equation as
\[2Al(s) + Fe_2O_3(s) \rightarrow 2Fe(s) + Al_2O_3(s) + \text{heat} \tag{7.5.2}\]
to indicate that heat is one of the products. Chemical equations in which heat is shown as either a reactant or a product are called thermochemical equations. In this reaction, the system consists of aluminum, iron, and oxygen atoms; everything else, including the container, makes up the surroundings. During the reaction, so much heat is produced that the iron liquefies. Eventually, the system cools; the iron solidifies as heat is transferred to the surroundings.A process in which heat (q) is transferred from a system to its surroundings is described as exothermic. By convention, \(q < 0\) for an exothermic reaction.
When you hold an ice cube in your hand, heat from the surroundings (including your hand) is transferred to the system (the ice), causing the ice to melt and your hand to become cold. We can describe this process by the following thermochemical equation:
\[ heat + H_2O_{(s)} \rightarrow H_2O_{(l)} \tag{7.5.3}\]
When heat is transferred to a system from its surroundings, the process is endothermic. By convention, \(q > 0\) for an endothermic reaction.
Technically, it is poor form to have a \(heat\) term in the chemical reaction like in Equations 7.5.2 and 7.5.3 since is it not a true species in the reaction. However, this is a convenient approach to represent exothermic and endothermic behavior and is commonly used by chemists.
The First Law
The relationship between the energy change of a system and that of its surroundings is given by the first law of thermodynamics, which states that the energy of the universe is constant. We can express this law mathematically as follows:
\[U_{univ}=ΔU_{sys}+ΔU_{surr}=0 \tag{7.5.4a}\]
where the subscripts univ, sys, and surr refer to the universe, the system, and the surroundings, respectively. Thus the change in energy of a system is identical in magnitude but opposite in sign to the change in energy of its surroundings.
The tendency of all systems, chemical or otherwise, is to move toward the state with the lowest possible energy.
An important factor that determines the outcome of a chemical reaction is the tendency of all systems, chemical or otherwise, to move toward the lowest possible overall energy state. As a brick dropped from a rooftop falls, its potential energy is converted to kinetic energy; when it reaches ground level, it has achieved a state of lower potential energy. Anyone nearby will notice that energy is transferred to the surroundings as the noise of the impact reverberates and the dust rises when the brick hits the ground. Similarly, if a spark ignites a mixture of isooctane and oxygen in an internal combustion engine, carbon dioxide and water form spontaneously, while potential energy (in the form of the relative positions of atoms in the molecules) is released to the surroundings as heat and work. The internal energy content of the \(CO_2/H_2O\) product mixture is less than that of the isooctane \(O_2\) reactant mixture. The two cases differ, however, in the form in which the energy is released to the surroundings. In the case of the falling brick, the energy is transferred as work done on whatever happens to be in the path of the brick; in the case of burning isooctane, the energy can be released as solely heat (if the reaction is carried out in an open container) or as a mixture of heat and work (if the reaction is carried out in the cylinder of an internal combustion engine). Because heat and work are the only two ways in which energy can be transferred between a system and its surroundings, any change in the internal energy of the system is the sum of the heat transferred (q) and the work done (w):
\[ΔU_{sys} = q + w \tag{7.5.5}\]
Although \(q\) and \(w\) are not state functions on their own, their sum (\(ΔU_{sys}\)) is independent of the path taken and is therefore a state function. A major task for the designers of any machine that converts energy to work is to maximize the amount of work obtained and minimize the amount of energy released to the environment as heat. An example is the combustion of coal to produce electricity. Although the maximum amount of energy available from the process is fixed by the energy content of the reactants and the products, the fraction of that energy that can be used to perform useful work is not fixed. Because we focus almost exclusively on the changes in the energy of a system, we will not use “sys” as a subscript unless we need to distinguish explicitly between a system and its surroundings.
Although \(q\) and \(w\) are not state functions, their sum (\(ΔU_{sys}\)) is independent of the path taken and therefore is a state function.
A sample of an ideal gas in the cylinder of an engine is compressed from 400 mL to 50.0 mL during the compression stroke against a constant pressure of 8.00 atm. At the same time, 140 J of energy is transferred from the gas to the surroundings as heat. What is the total change in the internal energy (ΔU) of the gas in joules?
Given: initial volume, final volume, external pressure, and quantity of energy transferred as heat
Asked for: total change in internal energy
Strategy:
- Determine the sign of \(q\) to use in Equation 7.5.5.
- From Equation 7.5.5 calculate \(w\) from the values given. Substitute this value into Equation 7.5.5 to calculate \(ΔU\).
Solution
A From Equation 7.5.5, we know that ΔU = q + w. We are given the magnitude of q (140 J) and need only determine its sign. Because energy is transferred from the system (the gas) to the surroundings, q is negative by convention.
B Because the gas is being compressed, we know that work is being done on the system, so \(w\) must be positive. From Equation 7.5.5,
Thus
ΔU = q + w = −140 J + 284 J = 144 J
In this case, although work is done on the gas, increasing its internal energy, heat flows from the system to the surroundings, decreasing its internal energy by 144 J. The work done and the heat transferred can have opposite signs.
A sample of an ideal gas is allowed to expand from an initial volume of 0.200 L to a final volume of 3.50 L against a constant external pressure of 0.995 atm. At the same time, 117 J of heat is transferred from the surroundings to the gas. What is the total change in the internal energy (ΔU) of the gas in joules?
Answer: −216 J
By convention, both heat flow and work have a negative sign when energy is transferred from a system to its surroundings and vice versa.
Summary
- Enthalpy is a state function, and the change in enthalpy of a system is equal to the sum of the change in the internal energy of the system and the PV work done.
The first law of thermodynamics states that the energy of the universe is constant. The change in the internal energy of a system is the sum of the heat transferred and the work done. At constant pressure, heat flow (q) and internal energy (U) are related to the system’s enthalpy (H). The heat flow is equal to the change in the internal energy of the system plus the PV work done. When the volume of a system is constant, changes in its internal energy can be calculated by substituting the ideal gas law into the equation for ΔU.

