15.5: Thermodynamics of Mixing and Dilution
- Page ID
- 3599
The free energy of a pure liquid or solid at 1 atm pressure is just its molar free energy of formation ΔG multiplied by the number of moles present. For gases and substances in solution, we have to take into account the concentration (which, in the case of gases, is normally expressed in terms of the pressure). We know that the lower the concentration, the greater the entropy, and thus the smaller the free energy. The following excerpt from this lesson serves as the starting point for the rest of the present lesson.
Entropy Depends on Concentration
As a substance becomes more dispersed in space, the thermal energy it carries is also spread over a larger volume, leading to an increase in its entropy. Because entropy, like energy, is an extensive property, a dilute solution of a given substance may well possess a smaller entropy than the same volume of a more concentrated solution, but the entropy per mole of solute (the molar entropy) will of course always increase as the solution becomes more dilute.
For gaseous substances, the volume and pressure are respectively direct and inverse measures of concentration. For an ideal gas that expands at a constant temperature (meaning that it absorbs heat from the surroundings to compensate for the work it does during the expansion), the increase in entropy is given by
\[\Delta S = R\ln \left( \dfrac{V_2}{V_1} \right) \label{2-4}\]
(If the gas is allowed to cool during the expansion, the relation becomes more complicated and will best be discussed in a more advanced course.)
Because the pressure of a gas is inversely proportional to its volume, we can easily alter the above relation to express the entropy change associated with a change in the pressure of a perfect gas:
\[\Delta S = R\ln \left( \dfrac{P_1}{P_2} \right) \label{2-5}\]
Expressing the entropy change directly in concentrations \(c\), we have the similar relation
\[\Delta S = R\ln \left( \dfrac{C_1}{C_2} \right) \label{2-6}\]
Although these equations strictly apply only to perfect gases and cannot be used at all for liquids and solids, it turns out that in a dilute solution, the solute can often be treated as a gas dispersed in the volume of the solution, so the last equation can actually give a fairly accurate value for the entropy of dilution of a solution. We will see later that this has important consequences in determining the equilibrium concentrations in a homogeneous reaction mixture.
The Gibbs energy of a Gas: standard states
The pressure of a perfect gas does not affect its enthalpy, but it does affect the entropy (box at left), and thus, through the –TΔS term, the free energy. When the pressure of such a gas changes from \(P_1\) to \(P_2\), the Gibbs energy change is
\[ \Delta G = \Delta H - T \Delta S = 0 - RT \ln \left( \dfrac{P_1}{P_2} \right) \label{4.8}\]
How can we evaluate the free energy of a specific sample of a gas at some arbitrary pressure? First, recall that the standard molar free energy G° that you would look up in a table refers to a pressure of 1 atm. The free energy per mole of our sample is just the sum of this value and any change in free energy that would occur if the pressure were changed from 1 atm to the pressure of interest
\[ G = G^o + RT \ln \left( \dfrac{P_1}{1\; atm} \right) \label{4.9}\]
which we normally write in abbreviated form
\[G = G^o + RT \ln P \label{4-10}\]
The term escaping tendency is not commonly used in traditional thermodynamics because it is essentially synonymous with the free energy, but it is worth knowing because it helps us appreciate the physical significance of free energy in certain contexts. The higher the pressure of a gas, the greater will be the tendency of its molecules to leave the confines of the container; we will call this the escaping tendency. The above equation tells us that the pressure of a gas is a directly observable measure of its free energy (G, not G°!). Combining these two ideas, we can say that the free energy of a gas is also a measure of its escaping tendency.
From Gases to Solutions: Mixing and Dilution
All substances, given the opportunity to form a homogeneous mixture with other substances, will tend to become more dilute. This can be rationalized simply from elementary statistics; there are more equally probable ways of arranging one hundred black marbles and one hundred white marbles, than two hundred marbles of a single color. For massive objects like marbles this has nothing to do with entropy, of course. However, when we are dealing with huge numbers of molecules capable of storing, exchanging and spreading thermal energy, mixing and expansion are definitely entropy-driven processes.
It can be argued, in fact, that mixing and expansion are really very similar; after all, when we mix two gases, each is expanding into the space formerly occupied exclusively by the other.
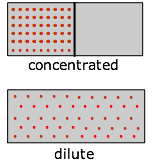
Suppose, for example, that we have a gas initially confined to one half of a box, and we then remove the barrier so that it can expand into the full volume of the container. We know that the entropy of the gas will increase as the thermal energy of its molecules spreads into the enlarged space; the actual increase, according to Equations \(\ref{2-4}\) and \(\ref{2-5}\) above, is \(R \ln 2\). And from Equation \(\ref{4-10}\), the change in \(G\) will be \(–RT \ln 2\).
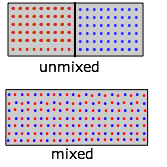
Now let us repeat the experiment, but starting this time with "red" molecules in one half of the container and "blue" ones in the right half. Because we now have two gases expanding into twice their initial volumes, the changes in S and G will be twice as great:
\[ΔS = 2 R \ln 2\]
\[ΔG = –2 RT \ln 2\]
However, notice that although each gas underwent an expansion, the overall process in this case is equivalent to mixing.
What is true for gaseous molecules can, in principle, apply also to solute molecules dissolved in a solvent. An important qualification here is that the solution must be an ideal one, meaning that the strength of interactions between all type of molecules (solutes A and B, and the solvent) must be the same. Remember that the enthalpy associated with the expansion of a perfect gas is by definition zero. In contrast, the \(ΔH_{mixing}\) of two liquids or of dissolving a solute in a solvent have finite values which may limit the miscibility of liquids or the solubility of a solute.
Given this proviso, we can define the Gibbs energy of dilution or mixing by substituting this equation into the definition of ΔG:
\[ \Delta G_{dilution} = \Delta H_{dilution} - RT\ln \left( \dfrac{C_1}{C_2} \right) \label{4-11}\]
If the substance in question forms an ideal solution with the other components, then \(ΔH_{diution}\) is zero, and we can write
\[ \Delta G_{dilution} = RT\ln \left( \dfrac{C_2}{C_1} \right) \label{4-12}\]
These relations tell us that the dilution of a substance from an initial concentration \(C_1\) to a more dilute concentration \(C_2\) is accompanied by a decrease in the free energy, and thus will occur spontaneously. By the same token, the spontaneous “un-dilution” of a solution will not occur (we do not expect the tea to diffuse back into the tea bag!) However, un-dilution can be forced to occur if some means can be found to supply to the system an amount of energy (in the form of work) equal to \(\Delta G_{dilution} \).
An important practical example of this is the metabolic work performed by the kidneys in concentrating substances from the blood for excretion in the urine.
To find the Gibbs energy of a solute at some arbitrary concentration, we proceed in very much the same way as we did for a gas: we take the sum of the standard free energy plus any change in the free energy that would accompany a change in concentration from the standard state to the actual state of the solution. From Equation \(\ref{4-12}\) it is easy to derive an expression analogous to Equation \(\ref{4-10}\):
\[G = G^o + RT \ln C \label{4-13}\]
which gives the free energy of a solute at some arbitrary concentration \(C\) in terms of its value \(G^o\) in its standard state.
Although Equation \(\ref{4-13}\) has the same simple form as Equation \(\ref{4-10}\), its practical application is fraught with difficulties, the major one being that it does not usually give values of \(G\) that are consistent with experiment, especially for solutes that are ionic or are slightly soluble. This is because most solutions (especially those containing dissolved ions) are far from ideal; intermolecular interactions between solute molecules and between solute and solvent bring back the enthalpy term that we left out in deriving Equation \(\ref{4-12}\). In addition, the structural organization of the solution becomes concentration dependent, so that the entropy depends on concentration in a more complicated way than is implied by the concentration analog of Equation \(\ref{4-12}\).
Chemical Reactions and Mixing
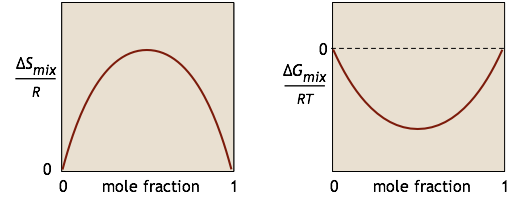
We characterize the tendency for a chemical reaction A → B to occur at constant temperature and pressure by the value of its standard Gibbs energy change ΔG°. If this quantity is negative, we know that the reaction will take place spontaneously. However, have you ever wondered why it is that substance A is not completely transformed into B if the latter is thermodynamically more stable? The answer is that if the reaction takes place in a single phase (gas or liquid), something else is going on: A and B are mixing together, and this process creates its own Gibbs energy change \(ΔG_{mixing}\). For a simple binary mixture of A and B (without any reaction), the changes in \(S\) and \(G\) can be represented by these simple plots:
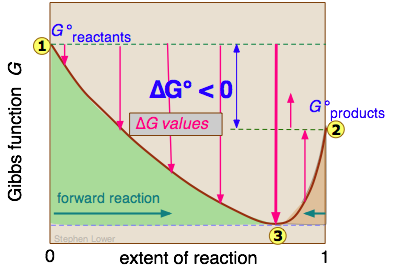
We will not try to prove it here, but it turns out that no matter how much lower the Gibbs energy of the products compared to that of the reactants, the free energy of the system can always be reduced even more if some of the reactants remain in the solution to contribute a ΔGmixing term. This is the reason that a plot of G as a function of the composition of such a system has a minimum at some point short of complete conversion.
Diffusion refers to the transport of a substance across a concentration gradient. The direction is always toward the region of lower concentration. You should now see that from a thermodynamic standpoint, these processes are identical in that they both represent the spontaneous "escape" of molecules from a region of higher concentration (lower entropy, higher Gibbs energy) to a region of lower concentration.
Instead of complicating G° by trying to correct for all of these effects, chemists have chosen to retain its simple form by making a single small change in the form of \(\ref{4-13}\):
\[G = G^o + RT \ln a \label{4-14}\]
This equation is guaranteed to work, because a, the activity of the solute, is its thermodynamically effective concentration. The relation between the activity and the concentration is given by
\[a = \gamma c \label{4-15}\]
where \(\gamma\) is the activity coefficient. As the solution becomes more dilute, the activity coefficient approaches unity:
\[ \lim _{c \rightarrow 0} \gamma =1 \label{4.16}\]
The price we pay for this simplicity is that the relation between the concentration and the activity at higher concentrations can be quite complicated, and must be determined experimentally for every different solution.
The question of what standard state we choose for the solute (that is, at what concentration is G° defined, and in what units is it expressed?) is one that you will wish you had never asked. We might be tempted to use a concentration of 1 molar, but a solution this concentrated would be subject to all kinds of intermolecular interaction effects, and would not make a very practical standard state. These effects could be eliminated by going to the opposite extreme of an “infinitely dilute” solution, but by Equation \(\ref{4-12}\) this would imply a free energy of minus infinity for the solute, which would be awkward. Chemists have therefore agreed to define the standard state of a solute as one in which the concentration is 1 molar, but all solute-solute interactions are magically switched off, so that \(\gamma\) is effectively unity. Since this is impossible, no solution corresponding to this standard state can actually exist, but this turns out to be only a small drawback, and seems to be the best compromise between convenience, utility, and reality.


