9.1: Three Views of Chemical Bonding
- Page ID
- 3520
Chemical bonds form when electrons can be simultaneously close to two or more nuclei, but beyond this, there is no simple, easily understood theory that would not only explain why atoms bind together to form molecules, but would also predict the three-dimensional structures of the resulting compounds as well as the energies and other properties of the bonds themselves. Unfortunately, no one theory exists that accomplishes these goals in a satisfactory way for all of the many categories of compounds that are known. Moreover, it seems likely that if such a theory does ever come into being, it will be far from simple.
When we are faced with a scientific problem of this complexity, experience has shown that it is often more useful to concentrate instead on developing models. A scientific model is something like a theory in that it should be able to explain observed phenomena and to make useful predictions. But whereas a theory can be discredited by a single contradictory case, a model can be useful even if it does not encompass all instances of the phenomena it attempts to explain. We do not even require that a model be a credible representation of reality; all we ask is that be able to explain the behavior of those cases to which it is applicable in terms that are consistent with the model itself. An example of a model that you may already know about is the kinetic molecular theory of gases. Despite its name, this is really a model (at least at the level that beginning students use it) because it does not even try to explain the observed behavior of real gases. Nevertheless, it serves as a tool for developing our understanding of gases, and as a starting point for more elaborate treatments.
Given the extraordinary variety of ways in which atoms combine into aggregates, it should come as no surprise that a number of useful bonding models have been developed. Most of them apply only to certain classes of compounds, or attempt to explain only a restricted range of phenomena. In this section we will provide brief descriptions of some of the bonding models; the more important of these will be treated in much more detail in later parts of this chapter.
Classical models
By classical, we mean models that do not take into account the quantum behavior of small particles, notably the electron. These models generally assume that electrons and ions behave as point charges which attract and repel according to the laws of electrostatics. Although this completely ignores what has been learned about the nature of the electron since the development of quantum theory in the 1920's, these classical models have not only proven extremely useful, but the major ones also serve as the basis for the chemist's general classification of compounds into "covalent" and "ionic" categories.
Electrostatic (Ionic Bonding)
Ever since the discovery early in the 19th century that solutions of salts and other electrolytes conduct electric current, there has been general agreement that the forces that hold atoms together must be electrical in nature. Electrolytic solutions contain ions having opposite electrical charges, opposite charges attract, so perhaps the substances from which these ions come consist of positive and negatively charged atoms held together by electrostatic attraction.
It turns out that this is not true generally, but a model built on this assumption does a fairly good job of explaining a rather small but important class of compounds that are called ionic solids. The most well known example of such a compound is sodium chloride, which consists of two interpenetrating lattices of Na+ and Cl– ions arranged in such as way that every ion of one type is surrounded (in three dimensional space) by six ions of opposite charge.
The main limitation of this model is that it applies really well only to the small class of solids composed of Group 1 and 2 elements with highly electronegative elements such as the halogens. Although compounds such as CuCl2 dissociate into ions when they dissolve in water, the fundamental units making up the solid are more like polymeric chains of covalently-bound CuCl2 molecules that have little ionic character.
Shared-Electrons (Covalent Bonding)
This model originated with the theory developed by G.N. Lewis in 1916, and it remains the most widely-used model of chemical bonding. The essential element s of this model can best be understood by examining the simplest possible molecule. This is the hydrogen molecule ion H2+, which consists of two nuclei and one electron. First, however, think what would happen if we tried to make the even simpler molecule H22+. Since this would consist only of two protons whose electrostatic charges would repel each other at all distances, it is clear that such a molecule cannot exist; something more than two nuclei are required for bonding to occur.
In the hydrogen molecule ion H2+ we have a third particle, an electron. The effect of this electron will depend on its location with respect to the two nuclei. If the electron is in the space between the two nuclei, it will attract both protons toward itself, and thus toward each other. If the total attraction energy exceeds the internuclear repulsion, there will be a net bonding effect and the molecule will be stable. If, on the other hand, the electron is off to one side, it will attract both nuclei, but it will attract the closer one much more strongly, owing to the inverse-square nature of Coulomb's law. As a consequence, the electron will now help the electrostatic repulsion to push the two nuclei apart.
We see, then, that the electron is an essential component of a chemical bond, but that it must be in the right place: between the two nuclei. Coulomb's law can be used to calculate the forces experienced by the two nuclei for various positions of the electron. This allows us to define two regions of space about the nuclei, as shown in the figure. One region, the binding region, depicts locations at which the electron exerts a net binding effect on the new nuclei. Outside of this, in the antibinding region, the electron will actually work against binding.
This simple picture illustrates the number one rule of chemical bonding: chemical bonds form when electrons can be simultaneously close to two or more nuclei. It should be pointed out that this principle applies also to the ionic model; as will be explained later in this chapter, the electron that is "lost" by a positive ion ends up being closer to more nuclei (including the one from whose electron cloud it came) in the compound.
- The polar covalent model: A purely covalent bond can only be guaranteed when the electronegativities (electron-attracting powers) of the two atoms are identical. When atoms having different electronegativities are joined, the electrons shared between them will be displaced toward the more electronegative atom, conferring a polarity on the bond which can be described in terms of percent ionic character. The polar covalent model is thus an generalization of covalent bonding to include a very wide range of behavior.
- The Coulombic model: This is an extension of the ionic model to compounds that are ordinarily considered to be non-ionic. Combined hydrogen is always considered to exist as the hydride ion H–, so that methane can be treated as if it were C4+ H–4. This is not as bizarre as it might seem at first if you recall that the proton has almost no significant size, so that it is essentially embedded in an electron pair when it is joined to another atom in a covalent bond. This model, which is not as well known as it deserves to be, has considerable predictive power, both as to bond energies and structures.
- The VSEPR model: The "valence shell electron repulsion" model is not so much a model of chemical bonding as a scheme for explaining the shapes of molecules. It is based on the quantum mechanical view that bonds represent electron clouds- physical regions of negative electric charge that repel each other and thus try to stay as far apart as possible.
Quantum Models
Quantum models of bonding take into account the fact that a particle as light a the electron cannot really be said to be in any single location. The best we can do is define a region of space in which the probability of finding the electron has some arbitrary value which will always be less than unity. The shape of this volume of space is called an orbital and is defined by a mathematical function that relates the probability to the (x,y,z) coordinates of the molecule. Like other models of bonding, the quantum models attempt to show how more electrons can be simultaneously close to more nuclei. Instead of doing so through purely geometrical arguments, they attempt this by predicting the nature of the orbitals which the valence electrons occupy in joined atoms.
- The hybrid orbital model: This was developed by Linus Pauling in 1931 and was the first quantum-based model of bonding. It is based on the premise that if the atomic s, p, and d orbitals occupied by the valence electrons of adjacent atoms are combined in a suitable way, the hybrid orbitals that result will have the character and directional properties that are consistent with the bonding pattern in the molecule. The rules for bringing about these combinations turn out to be remarkably simple, so once they were worked out it became possible to use this model to predict the bonding behavior in a wide variety of molecules. The hybrid orbital model is most usefully applied to the p-block elements the first two rows of the periodic table, and is especially important in organic chemistry.
- The molecular orbital model: This model takes a more fundamental approach by regarding a molecule as a collection of valence electrons and positive cores. Just as the nature of atomic orbitals derives from the spherical symmetry of the atom, so will the properties of these new molecular orbitals be controlled by the interaction of the valence electrons with the multiple positive centers of these atomic cores. These new orbitals, unlike those of the hybrid model, are delocalized; that is, they do not "belong" to any one atom but extend over the entire region of space that encompasses the bonded atoms. The available (valence) electrons then fill these orbitals from the lowest to the highest, very much as in the Aufbau principle that you learned for working out atomic electron configurations. For small molecules (which are the only ones we will consider here), there are simple rules that govern the way that atomic orbitals transform themselves into molecular orbitals as the separate atoms are brought together. The real power of molecular orbital theory, however, comes from its mathematical formation which lends itself to detailed predictions of bond energies and other properties.
- The electron-tunneling model: A common theme uniting all of the models we have discussed is that bonding depends on the fall in potential energy that occurs when opposite charges are brought together. In the case of covalent bonds, the shared electron pair acts as a kind of "electron glue" between the joined nuclei. In 1962, however, it was shown that this assumption is not strictly correct, and that instead of being concentrated in the space between the nuclei, the electron orbitals become even more concentrated around the bonded nuclei. At the same time however, they are free to "move" between the two nuclei by a process known as tunneling. This refers to a well-known quantum mechanical effect that allows electrons (or other particles small enough to exhibit wavelike properties) to pass ("tunnel") through a barrier separating two closely adjacent regions of low potential energy. One result of this is that the effective volume of space available to the electron is increased, and according to the uncertainty principle this will reduce the kinetic energy of the electron.
The electron-tunneling model
According to this model, the bonding electrons act as a kind of fluid that concentrates in the region of each nucleus (lowering the potential energy) and at the same time is able to freely flow between them (reducing the kinetic energy). A summary of the concept, showing its application to a simple molecule, is shown on the next page. Despite its conceptual simplicity and full acknowledgment of the laws of quantum mechanics, this model is not widely known and is rarely taught.
Chemical bonding occurs when one or more electrons can be simultaneously close to two nuclei. But how can this be arranged? The conventional picture of the shared electron bond places the bonding electrons in the region between the two nuclei. This makes a nice picture, but it is not consistent with the principle that opposite charges attract. This would imply that the electrons would be "happiest" (at the lowest potential energy) when they are very close to a nucleus, not half a bond-length away from two of them!
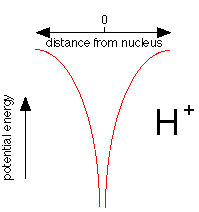
This plot shows how the potential energy of an electron in the hydrogen atom varies with its distance from the nucleus. Notice how the energy falls without limit as the electron approaches the nucleus, represented here as a proton, \(H^+\). If potential energy were the only consideration, the electron would fall right into the nucleus where its potential energy would be minus infinity.
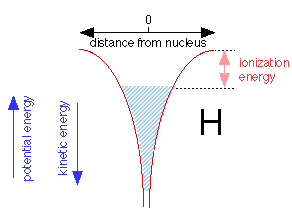
When an electron is added to the proton to make a neutral hydrogen atom, it tries to get as close to the nucleus as possible. The Heisenberg uncertainty principle requires the total energy of the electron energy to increase as the volume of space it occupies diminishes. As the electron gets closer to the nucleus, the nuclear charge confines the electron to such a tiny volume of space that its energy rises, allowing it to "float" slightly away from the nucleus without ever falling into it.
The shaded region above shows the range of energies and distances from the nucleus the electron is able to assume within the 1s orbital. The electron can thus be regarded as a fluid that occupies a vessel whose walls conform to the red potential energy curves shown above. Note that as the potential energy falls, the kinetic energy increases, but only half as fast (this is called the virial theorem). Thus close to the nucleus, the kinetic energy is large and so is the electron's effective velocity. The top of the shaded area defines the work required to raise its potential energy to zero, thus removing it from the atom; this corresponds, of course, to the ionization energy.
The Tunneling Effect
A quantum particle can be described by a waveform which is the plot of a mathematical function related to the probability of finding the particle at a given location at any time. If the particle is confined to a box, it turns out that the wave does not fall to zero at the walls of the box, but has a finite probability of being found outside it. This means that a quantum particle is able to penetrate, or "tunnel through" its confining boundaries. This remarkable property is called the tunnel effect.
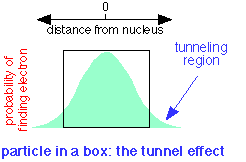
In terms of the electron fluid model introduced above, the fluid is able to "leak out" of the atom if another low-energy location can be found nearby.
Electron tunneling in the simplest molecule
Suppose we now bring a bare proton up close to a hydrogen atom. Each nucleus has its own potential well, but only that of the hydrogen atom is filled, as indicated by the shading in the leftmost potential well.
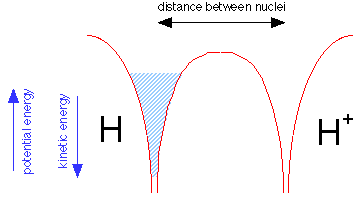
But the electron fluid is able to tunnel through the potential energy barrier separating the two wells; like any liquid, it will seek a common level in the two sides of the container as shown below. The electron is now "simultaneously close to two nuclei" while never being in between them. Bear in mind that this would be physically impossible for a real liquid composed of real molecules; this is purely a quantum effect that is restricted to a low-mass particle such as the electron.
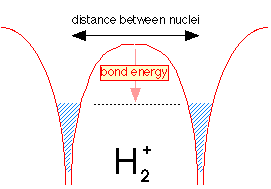
Because the same amount of electron fluid is now shared between the two wells, its level in both is lower. The difference between what it is now and what is was before corresponds to the bond energy of the hydrogen molecule ion.
The dihydrogen molecule
Now let's make a molecule of dihydrogen. We start with two hydrogen atoms, each with one electron. But there is a problem here: both potential energy wells are already filled with electron fluid; there is no room for any more without pushing the energy way up.
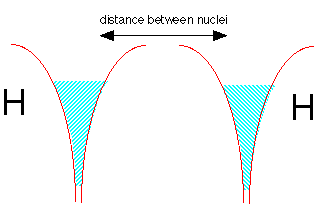
But quantum theory again comes to the rescue! If the two electrons have opposite spins, the two fluids are able to interpenetrate each other, very much as two gases are able to occupy the same container. This is depicted by the double shading in the diagram below.
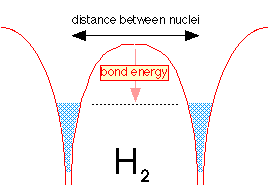
When the two hydrogen atoms are within tunneling distance, half of the electron fluid (really the probability of finding the electron) from each well flows into the other well. Because the two fluids are able to interpenetrate, the level is not much different from what it was in the H2+ ion, but the greater density of the electron-fluid between the two nuclei makes H2 a strongly bound molecule.
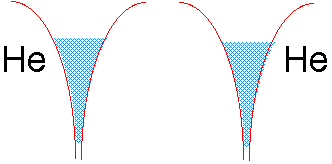
So why does dihelium not exist?
If we tried to join two helium atoms in this way, we would be in trouble. The electron well of He already contains two electrons of opposite spin. There is no room for more electron fluid (without raising the energy), and thus no way the electrons in either He atom can be simultaneously close to two nuclei.
Ionic Bonding
Even before G.N.Lewis developed his theory of the shared electron pair bond, it was believed that bonding in many solid salts could be satisfactorily explained on the basis of simple electrostatic forces between the positive and negative ions which are assumed to be the basic molecular units of these compounds. Lewis himself continued to recognize this distinction, which has continued to be a part of the tradition of chemistry; the shared electron pair bond is known as the covalent bond, while the other type is the ionic or electrovalent bond.
The covalent bond is formed when two atoms are able to share electrons:
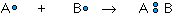
whereas the ionic bond is formed when the "sharing" is so unequal that an electron from atom A is completely lost to atom B, resulting in a pair of ions:
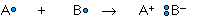
The two extremes of electron sharing represented by the covalent and ionic models appear to be generally consistent with the observed properties of molecular and ionic solids and liquids. But does this mean that there are really two kinds of chemical bonds, ionic and covalent?
Bonding in ionic solids
According to the ionic electrostatic model, solids such as NaCl consist of positive and negative ions arranged in a crystal lattice. Each ion is attracted to neighboring ions of opposite charge, and is repelled by ions of like charge; this combination of attractions and repulsions, acting in all directions, causes the ion to be tightly fixed in its own location in the crystal lattice.
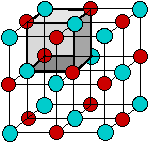
Since electrostatic forces are nondirectional, the structure of an ionic solid is determined purely by geometry: two kinds of ions, each with its own radius, will fall into whatever repeating pattern will achieve the lowest possible potential energy. Surprisingly, there are only a small number of possible structures.
Is there such as thing as a "purely" ionic bond?
When two elements form an ionic compound, is an electron really lost by one atom and transferred to the other one? In order to deal with this question, consider the data on the ionic solid LiF. The average radius of the neutral Li atom is about 2.52Å.
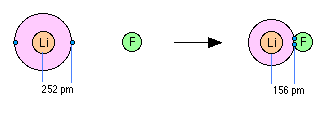
Now if this Li atom reacts with an atom of F to form LiF, what is the average distance between the Li nucleus and the electron it has "lost" to the fluorine atom? The answer is 1.56Å; the electron is now closer to the lithium nucleus than it was in neutral lithium! So the answer to the above question is both yes and no: yes, the electron that was now in the 2s orbital of Li is now within the grasp of a fluorine 2p orbital, but no, the electron is now even closer to the Li nucleus than before, so how can it be "lost"? The one thing that is inarguably true about LiF is that there are more electrons closer to positive nuclei than there are in the separated Li and F atoms. But this is just the condition that gives rise to all forms of chemical bonding:
Chemical bonds form when electrons can be simultaneously near two or more nuclei
It is obvious that the electron-pair bond brings about this situation, and this is the reason for the stability of the covalent bond. What is not so obvious (until you look at the numbers such as were quoted for LiF above) is that the "ionic" bond results in the same condition; even in the most highly ionic compounds, both electrons are close to both nuclei, and the resulting mutual attractions bind the nuclei together. This being the case, is there really any fundamental difference between the ionic and covalent bond?
The answer, according to modern chemical thinking is probably "no"; in fact, there is some question as to whether it is realistic to consider that these solids consist of "ions" in the usual sense. The preferred picture that seems to be emerging is one in which the electron orbitals of adjacent atom pairs are simply skewed so as to place more electron density around the "negative" element than around the "positive" one.
This being said, it must be reiterated that the ionic model of bonding is a useful one for many purposes, and there is nothing wrong with using the term "ionic bond" to describe the interactions between the atoms in "ionic solids" such as LiF and NaCl.
Polar covalence
If there is no such thing as a "completely ionic" bond, can we have one that is completely covalent? The answer is yes, if the two nuclei have equal electron attracting powers. This situation is guaranteed to be the case with homonuclear diatomic molecules— molecules consisting of two identical atoms. Thus in Cl2, O2, and H2, electron sharing between the two identical atoms must be exactly even; in such molecules, the center of positive charge corresponds exactly to the center of negative charge: halfway between the two nuclei.
Electronegativity
This term was introduced earlier in the course to denote the relative electron-attracting power of an atom. The electronegativity is not the same as the electron affinity; the latter measures the amount of energy released when an electron from an external source "falls into" a vacancy within the outermost orbital of the atom to yield an isolated negative ion.
The products of bond formation, in contrast, are not ions and they are not isolated; the two nuclei are now drawn closely together by attraction to the region of high electron density between them. Any shift of electron density toward one atom takes place at the energetic expense of stealing it from the other atom.
It is important to understand that electronegativity is not a measurable property of an atom in the sense that ionization energies and electron affinity are; electronegativity is a property that an atom displays when it is bonded to another. Any measurement one does make must necessarily depend on the properties of both of the atoms.
By convention, electronegativities are measured on a scale on which the highest value, 4.0, is arbitrarily assigned to fluorine. A number of electronegativity scales have been proposed, each based on slightly different criteria. The most well known of these is due to Linus Pauling, and is based on a study of bond energies in a variety of compounds.
The periodic trends in electronegativity are about what one would expect; the higher the nuclear charge and the smaller the atom, the more strongly attractive will it be to an outer-shell electron of an atom within binding distance. The division between the metallic and nonmetallic elements is largely that between those that have Pauling electronegativies greater than about 1.7, and those that have smaller electronegativities.
The greater the electronegativity difference between two elements A and B, the more polar will be their molecule AB. It is important to point out, however, that the pairs having the greatest electronegativity differences, the alkali halides, are solids order ordinary conditions and exist as molecules only in the rarefied conditions of the gas phase. Even these ionic solids possess a certain amount of covalent character, so, as discussed above, there is no such thing as a "purely ionic" bond. It has become more common to place binary compounds on a scale something like that shown here, in which the degree of shading is a rough indication of the number of compounds at any point on the covalent-ionic scale.

Covalent or ionic: a false dichotomy
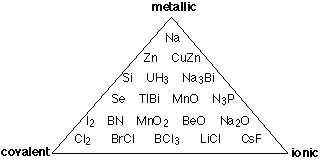
The covalent-ionic continuum described above is certainly an improvement over the old covalent -versus - ionic dichotomy that existed only in the textbook and classroom, but it is still only a one-dimensional view of a multidimensional world, and thus a view that hides more than it reveals. The main thing missing is any allowance for the type of bonding that occurs between more pairs of elements than any other: metallic bonding. Intermetallic compounds are rarely even mentioned in introductory courses, but since most of the elements are metals, there are a lot of them, and many play an important role in metallurgy. In metallic bonding, the valence electrons lose their association with individual atoms; they form what amounts to a mobile "electron fluid" that fills the space between the crystal lattice positions occupied by the atoms, (now essentially positive ions.) The more readily this electron delocalization occurs, the more "metallic" the element.
Thus instead of the one-dimension chart shown above, we can construct a triangular diagram whose corners represent the three extremes of "pure" covalent, ionic, and metallic bonding.
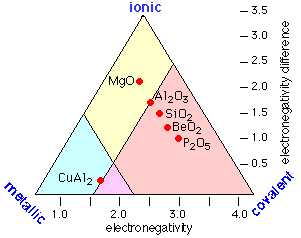
We can take this a step farther by taking into account collection of weaker binding effects known generally as van der Waals forces. Contrary to what is often implied in introductory textbooks, these are the major binding forces in most of the common salts that are not alkali halides; these include NaOH, CaCl2, MgSO4. They are also significant in solids such as CuCl2 and solid SO3 in which infinite covalently-bound chains are held together by ion-induced dipole and similar forces.
The only way to represent this four-dimensional bonding-type space in two dimensions is to draw a projection of a tetrahedron, each of its four corners representing the "pure" case of one type of bonding.
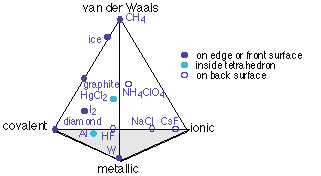
Note that some of the entries on this diagram (ice, CH4, and the two parts of NH4ClO4) are covalently bound units, and their placement refers to the binding between these units. Thus the H2O molecules in ice are held together mainly by hydrogen bonding, which is a van der Waals force, with only a small covalent contribution.
Note: the triangular and tetrahedral diagrams above were adapted from those in the excellent article by William B. Jensen, "Logic, history and the chemistry textbook", Part II, J. Chemical Education 1998: 817-828.


