15.10: Bond Enthalpies
- Page ID
- 49542
The heat changes which accompany a chemical reaction are caused largely by changes in the electronic energy of the molecules. If we restrict our attention to gases, and hence to fairly simple molecules, we can go quite a long way toward predicting whether a reaction will be exothermic by considering the bonds which are broken and made in the course of the reaction. In order to do this we must first become familiar with the idea of a bond enthalpy.
In other sections we point out that when a chemical bond forms, negative charges move closer to positive charges than before, and so there is a lowering of the energy of the molecule relative to the atoms from which it was made. This means that energy is required to break a molecule into its constituent atoms. The bond enthalpy DX–Y of a diatomic molecule X—Y is the enthalpy change for the (usually hypothetical) process:
\[\ce{XY(g) \rightarrow X(g) + Y(g)} \nonumber \] \[\Delta H^{o} (298 K) = D_{x-y} \nonumber \]
We have already used the term bond energy to describe this quantity, though strictly speaking the bond energy is a measure of ΔU rather than ΔH. As we have already seen, ΔU and ΔH are nearly equal, and so either term may be used.
As an example, let us consider the bond enthalpy for carbon monoxide. It is possible to establish the thermochemical equation
\[\ce{CO(g) \rightarrow C(g) + O(g)} \nonumber \]
\[\Delta H^{o}(298 K) = 1073 kJ mol^{-1}\label{3} \]
Accordingly we can write
\[\ce{C_{C\equiv O}= 1073 kJ mol^{-1}} \nonumber \]
even though the process to which Eq. \(\ref{3}\) corresponds is hypothetical: Neither carbon nor oxygen exists as a monatomic gas at 298 K. For triatomic and polyatomic molecules, the bond enthalpy is usually defined as a mean. In the case of water, for instance, we have
\[\ce{H_{2}O(g) \rightarrow 2H(g) + O(g)} \nonumber \]
\[\Delta H^{o} (298 K) = 927.2 \text{kJ mol}^{-1} \nonumber \]
Since it requires 927.2 kJ to break open two O—H bonds, we take half this value as the mean bond enthalpy and write
\[D_{O-H} = 463.6 \text{kJ mol}^{-1} \nonumber \]
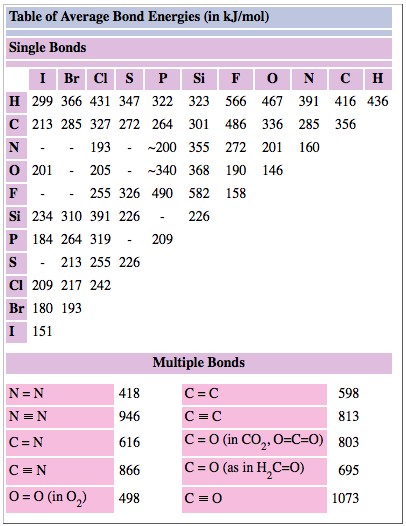
In methanol, CH3OH,however, a value of 427 kJ mol–1 for the O—H bond enthalpy fits the experimental data better. In other words the strength of the O—H varies somewhat from compound to compound. Because of this fact, we must expect to obtain only approximate results, accurate only to about ± 50 kJ mol–1, from the use of bond enthalpies. Bond enthalpies for both single and multiple bonds are given in Table \(\PageIndex{1}\).
TABLE \(\PageIndex{1}\) Average Bond Energies/kJ mol–1.
As an example of how a table of bond enthalpies can he used to predict the ΔH value for a reaction, let us take the simple case
\[\ce{H_{2}(g) + F_{2}(g) \rightarrow 2HF(g)}\label{9} \]
298 K, 1 atm
We can regard this reaction as occurring in two stages (Figure \(\PageIndex{1}\) ). In the first stage all the reactant molecules are broken up into atoms:
\[\ce{H_{2}(g) + F_{2}(g) \rightarrow 2H(g) + F(g)}\label{10} \] 298 K, 1 atm
For this stage
\[\Delta H_I = H_{H-H}+ D_{F-F}\label{11} \]
since 1 mol H2 and 1 mol F2 have been dissociated.
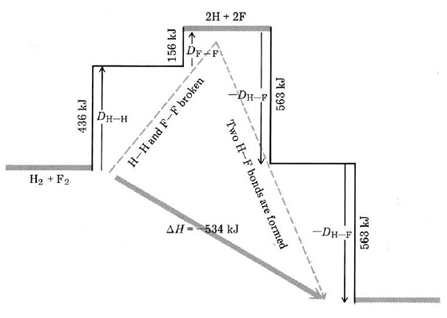
In the second stage the H and F atoms are reconstituted to form HF molecules:
\[\ce{2H(g) + 2F(g) \rightarrow 2HF(g)} \nonumber \] 298 K, 1 atm
For which
\[\Delta H_{II} = – 2D_{H-F} \nonumber \]
where a negative sign is necessary since this stage corresponds to the reverse of dissociation.
Since Eq. \(\ref{9}\) corresponds to the sum of Equations \(\ref{10}\) and \(\ref{11}\), Hess's law allows us to add ΔH values:
-
- \[\Delta H^{o}_{reaction} = \Delta H_{I} + \Delta H_{II} \nonumber \]
-
- \(= D_{H-H} + D_{F-F} – 2D{H-F}\)
- \(= (436 + 159 – 2 * 566) \text{kJ mol}^{-1}\)
- \(= –539 \text{kJ mol}^{-1}\)
We can work this same trick of subdividing a reaction into a bond-breaking stage followed by a bond-making stage for the general case of any gaseous reaction. In the first stage all the bonds joining the atoms in the reactant molecules are broken and a set of gaseous atoms results. For this stage
\[\Delta H_{I} = \sum_{\text{bonds broken}} D \nonumber \]
The enthalpy change is the sum of the bond enthalpies for all bonds broken. In the second stage these gaseous atoms are reconstituted into the product molecules. For this second stage therefore
\[\Delta H_{II} = – \sum_{\text{bonds formed}} D \nonumber \]
where the negative sign is necessary because the reverse of bond breaking is occurring in this stage. The total enthalpy change for the reaction at standard pressure is thus
\[\Delta H^{o} = \Delta H_{I} + \Delta H_{II} \nonumber \]
or
\[\Delta H^{o} = \sum D \text{(bond broken)} – \sum D \text{(bond formed)} \nonumber \]
The use of this equation is illustrated in the next example.
Using Table \(\PageIndex{1}\) calculate the value of ΔH°(298 K) for the reaction
\[\ce{CH_{4}(g) + 2O_{2}(g) \rightarrow CO_{2}(g) + 2H_{2}O(g)} \nonumber \]
Solution
It is best to sketch the molecules and their bonds in order to make sure that none are missed.
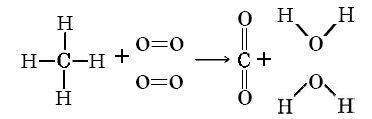
Thus \(\Delta H^{o} = \sum D \text{(bond broken)} – \sum D \text{(bond formed)}\)
\(= 4 D_{C\bond{-}H} + 2 D_{D\bond{=}D} - 2 D_{C\bond{=}O} - 4 D_{O\bond{-}H}\)
\(= (4 * 416 + 2 * 498 – 2 * 803 – 4 * 467) \text{kJ mol}^{-1}\)
\(= – 814 \text{kJ mol}^{-1}\)
The experimental value for this enthalpy change can be calculated from standard enthalpies of formation. It is –802.4 kJ mol–1. The discrepancy is due to the unavoidable use of mean bond enthalpies in the calculation.

