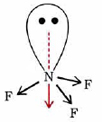
7.12: Polarity in Polyatomic Molecules
- Page ID
- 49391

When more than one polar bond is present in the same molecule, the polarity of one bond may cancel that of another. Thus the presence of polar bonds in a polyatomic molecule does not guarantee that the molecule as a whole will have a dipole moment. In such a case it is necessary to treat each polar bond mathematically as a vector and represent it with an arrow. The length of such an arrow shows how large the bond dipole moment is, while the direction of the arrow is a line drawn from the positive to the negative end of the bond. Adding the individual bond dipole moments as vectors will give the overall molecular dipole moment.
As an example of this vector addition, consider the BF3 molecule in Figure \(\PageIndex{1}\). The dipole moments of the three B―F bonds are represented by the arrows BF′ (pointing straight left), BF′′ (pointing down to the right), and BF′′′ (pointing up to the right). The sum of vectors BF′′ and BF′′′ may be obtained by the parallelogram law—a line from F′′′ drawn parallel to BF′′ intersects a line from F′′ drawn parallel to BF′′′ at point E. Thus the resultant vector BE (the diagonal of the parallelogram BF′′′EF′′) is the sum of BF′′ and BF′′′. The resultant BE is exactly equal in length and exactly opposite in direction to bond dipole BF′′. Therefore the net result is zero dipole moment.
Those arrangements of equivalent bonds that give zero dipole moment in this way are shown in Figure \(\PageIndex{2}\). In addition to the trigonal arrangement just discussed, there is the obvious case of two equal bonds 180° apart. The other is much less obvious, namely, a tetrahedral arrangement of equal bonds. Any combination of these arrangements will also be nonpolar. The molecule PF5 for example, is nonpolar since the bonds are arranged in a trigonal bipyramid, as discussed in "The Shapes of Molecules." Since three of the five bonds constitute a trigonal arrangement, they will have no resultant dipole moment. The remaining two bonds have equal but opposite dipoles which will likewise cancel.
If we replace any of the bonds shown in Figure \(\PageIndex{2}\) with a different bond, or with a lone pair, the vectors will no longer cancel and the molecule will have a resultant dipole moment.
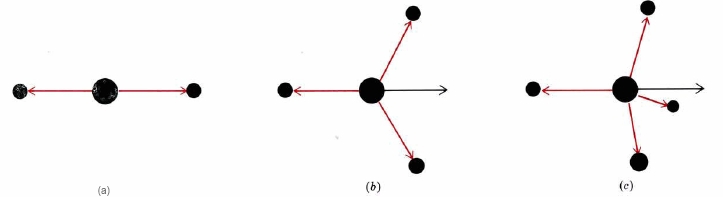
Figure \(\PageIndex{2}\) The simplest arrangements of equivalent bonds around a central atom which produce a resultant dipole moment of zero: (a) linear; (b) trigonal. The two right-hand bonds (black resultant) cancel the left-hand bond. (c) Tetrahedral. The three right-hand bonds (black resultant) cancel the left-hand bond.
The following jmols further illustrate the dipole moment concept. Click the Magnetic Dipole check box to see the dipole in place on the jmol. The first jmol of methane shows a molecule with no dipole. Each bond's dipole moment cancels, leading to a molecule without any net dipole.
This second jmol demonstrates the dipole when one hydrogen atom in methane is replaced by a highly electronegative fluorine. Fluorine pulls the electron strongly away from the carbon atom, creating a dipole moment pointing from carbon to fluorine.
The third jmol depicts the dipole moment when two hydrogen atoms in methane have been replaced by fluorine atoms. Each fluorine pulls the electrons in the carbon-fluorine bonds away from the carbon, creating a net dipole pointing between the two fluorine atoms.
Using this rule together with VSEPR theory, you can predict whether a molecule is polar or not. You can also make a rough estimate of how polar it will be.
Which of the following molecules are polar? About how large a dipole moment would you expect for each? (a) CF4; (b) CHF3; (c) H2O; (d)NF3.
Solution:
a) VSEPR theory predicts a tetrahedral geometry for CF4. Since all four bonds are the same, this molecule corresponds to Figure 2c. It has zero dipole moment.
b) For CHF3, VSEPR theory again predicts a tetrahedral geometry. However, all the bonds are not the same, and so there must be a resultant dipole moment. The C―H bond is essentially nonpolar, but the three C―F bonds are very polar and negative on the F side. Thus the molecule should have quite a large dipole moment:
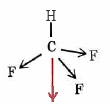
The resultant dipole is shown in color.
c) The O atom in H2O is surrounded by four electron pairs, two bonded to H atoms and two lone pairs. All four pairs are not equivalent, and so there is a resultant dipole. Since O is much more electronegative than H, the two O―H bonds will produce a partial negative charge on the O. The two lone pairs will only add to this effect.
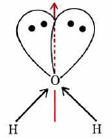
d) In NF3 the N atom is surrounded by four electron pairs in an approximately tetrahedral arrangement. Since all four pairs are not equivalent, the molecule is polar. The dipole moment, though, is surprisingly small because the lone pair cancels much of the polarity of the N―F bonds: