The second law of thermodynamics can be formulated in many ways, but in one way or another they are all related to the fact that the state function entropy, \(S\), tends to increase over time in isolated systems. For a long time, people have looked at the entire universe as an example of an isolated system and concluded that its entropy must be steadily increasing until \(\delta S_{universe}\) becomes zero. As we will see below, the second law has important consequences for the question of how we can use heat to do useful work.
Vacuum Expansion
Let's compare two expansions from \(V_1\) to \(V_2\) for an ideal gas, both are isothermal. The first is an irreversible one, where we pull a peg an let the piston move against vacuum:
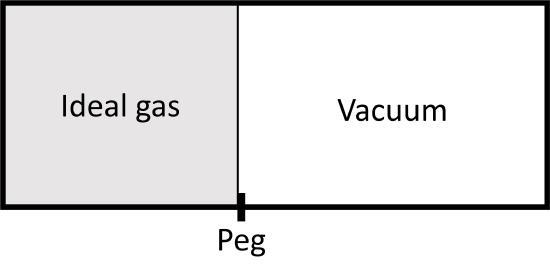
The second one is a reversible isothermal expansion from \(V_1\) to \(V_2\) (and \(P_1\) to \(P_2\)) that we have examined before. In both cases, the is no change in internal energy since \(T\) does not change. During the irreversible expansion, however, there is also no volume work because the piston is expanding against a vacuum and the following integral:
\[\int -P_{ext}dV = 0 \nonumber \]
integrates to zero. The piston has nothing to perform work against until it slams into the right hand wall. At this point \(V=V_2\) and then \(dV\) becomes zero. This is not true for the reversible isothermal expansion as the external pressure must always equal the internal pressure.
No energy and no work means no heat!
Clearly the zero heat is irreversible heat (\(q_{irr} = 0\)) and this makes it hard to calculate the entropy of this spontaneous process. But then this process ends in the same final state as the reversible expansion from \(V_1\) to \(V_2\). We know that \(dU\) is still zero, but now \(δw_{rev} = -δq_{rev}\) is nonzero. We calculated its value before:
\[q_{rev} = nRT \ln \left(\dfrac{V_2}{V_1} \right) \label{Vacuum} \]
The Claussius definition of entropy change can be used to find \(\Delta S\) (under constant temperature).
\[\Delta S = \dfrac{q_{rev}}{T} \label{Claussius}\]
Substituting Equation \(\ref{Vacuum}\) into Equation \ref{Claussius} results in
\[\Delta S = nR \ln \left(\dfrac{V_2}{V_1} \right) \nonumber \]
As \(S\) is a state function this equation also holds for the irreversible expansion against vacuum.
Always calculate the entropy difference between two points along a reversible path.
For the irreversible expansion into vacuum we see that
\[\begin{align*}\Delta S_\text{total} &= \Delta S_\text{sys} + \Delta S_\text{surr} \\[4pt] &= nR\ln \left( \dfrac{V_2}{V_1}\right) + 0 \\[4pt] &= nR\ln \left( \dfrac{V_2}{V_1}\right) \end{align*} \]
For the reversible expansion, heat is transferred to the system while the system does work on the surroundings in order to keep the process isothermal:
\[\begin{align*}\Delta S_\text{sys} &= nR\ln \left( \dfrac{V_2}{V_1}\right) \end{align*}\]
The entropy change for the surrounding is the opposite of the system:
\[\begin{align*}\Delta S_\text{surr} &= -nR\ln \left( \dfrac{V_2}{V_1}\right) \end{align*}\]
This is because the amount of heat transferred to the system is the same as the heat transferred from the surroundings and this process is reversible so the system and surroundings are at the same temperature (equilibrium). Heat is related to entropy by the following equation:
\[ dS = \frac{\delta q}{T} \]
Therefore, the total entropy change for the reversible process is zero:
\[\begin{align*}\Delta S_\text{total} &= \Delta S_\text{sys} + \Delta S_\text{surr} \\[4pt] &= nR\ln \left( \dfrac{V_2}{V_1}\right)- nR\ln \left( \dfrac{V_2}{V_1}\right) \\[4pt] &=0 \end{align*}\]
The Mixing of Two Gases
Consider two ideal gases at same pressure separated by a thin wall that is punctured. Both gases behave as if the other one is not there and again we get a spontaneous process, mixing in this case.
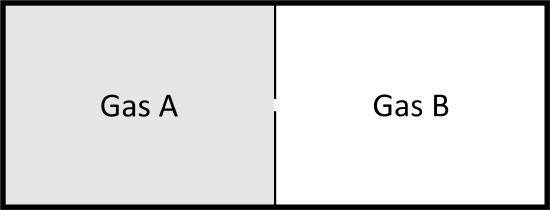
If the pressure is the same the number of moles of each gas should be proportional to the original volumes, \(V_A\) and \(V_B\), and the total number of moles to the total volume \(V_{tot}\).
For gas A we can write:
\[\Delta S_A = n_A R \ln \dfrac{V_{tot}}{V_A} = n_A R \ln \dfrac{n_{tot}}{n_A} \nonumber \]
and similarly for gas B we can write:
\[\Delta S_B = n_B R \ln \dfrac{V_{tot}}{V_B} = n_B R \ln \dfrac{n_{tot}}{n_B} \nonumber \]
The total entropy change is therefore the sum of constituent entropy changes:
\[ \Delta S = \Delta S_A + \Delta S_B \nonumber \]
and the entropy change total per mole of gas is:
\[ \dfrac{\Delta S}{n_{tot}} =R \dfrac{\left[n_B \ln \dfrac{n_{tot}}{n_B}+ n_A \ln \dfrac{n_{tot}}{n_A} \right ]}{n_{tot}} \label{EqTot} \]
Equation \(\ref{EqTot}\) can be simplified using mole fractions:
\[\chi_A = \dfrac{n_A}{n_{tot}} \nonumber \]
and the mathematical relationship of logarithms that:
\[\ln \left( \dfrac{x}{y} \right)= - \ln \left( \dfrac{y}{x} \right) \nonumber \]
to:
\[\Delta \bar{S} = -R \left [\chi_A\ln \chi_A +\chi_B \ln \chi_B \right] \label{Molar Entropy} \]
In the case of mixing of more than two gases, Equation \(\ref{Molar Entropy}\) can be expressed as:
\[\Delta \bar{S} = -R \sum \chi_i\ln \chi_i \label{Sum Entropy} \]
This entropy expressed in Equations \(\ref{Molar Entropy}\) and \(\ref{Sum Entropy}\) is known as the entropy of mixing; its existence is the major reason why there is such a thing as diffusion and mixing when gases, and also solutions (even solid ones), are brought into contact with each other.



