Lab 3: Fourier Transform Infrared Spectroscopy (FTIR)
- Page ID
- 136266
- Students should develop an understanding of molecular symmetry and vibrational modes.
- Students should be able to use symmetry elements to predict which vibrational modes are IR active.
- Student's should be able to use a solve the pollution mystery by determining the air pollutant and the source of the air pollutant.
Introduction
The procedure of this lab does not follow the normal format. In this lab, you have been hired by an environmental testing company to monitor air pollutants. By working through a series of exercises, you will gain important information to determine the air pollutant in an air sample and therefore determine the source of the pollution. The air sample was taken in a location 20 m away from an open farm field where strawberries were growing. In the field on one side, there were cows grazing; on the other side, there was a natural gas pumping station. Across the street, there was a gas station with an auto repair shop specializing in air conditioner repair and a dry cleaner. This information narrows the list of suspected chemicals to six. Test your air sample using an infrared spectrometer and determine the culprit.
The FTIR / Vibrational spectroscopy experiment is an adaptation of "Pollution Police" by Profs. Jodye Selco and Janet Beery at the University of Redlands, which was presented at the Division of Chemical Education Regional ACS meeting in Ontario, CA 1999. Many students currently in CHE 115 have already taken CHE 124A which focuses on symmetry, molecular vibrations, and point groups. For students that have taken CHE 124A, use this lab as an opportunity to use your knowledge and assist your lab partners that have not taken the class yet.
There are resources available to further an understanding of FTIR. The theory of FTIR spectrometer operation is discussed in SHN Chapters 16 and 17. The group theory and vibrational quantum mechanics are discussed in McQuarrie and Simon (Chem 110B text) Chapters 12 and 13. Principles of Infrared Spectrometry and its application can be found in Skoog, Holler, and Crouch (the textbook for CHE 115) in chapters 16 and 17.
The FTIR exercise follows the format of a detective story involving solving a series of problems rather than the normal lab format. The experimental portion of the exercises are problems #9 and #10. The computer in room 3475 will be used to complete problems #2, 7, and 8. The computers are set up to run HyperChem, Gaussian, and Spartan.
Setting the Scene
You have been hired by an environmental testing company to monitor air pollutants. Air pollutants can be released from many types of sources. A few examples of sources are: factories, cars, or cattle. Sometimes, volatile chemicals can evaporate from agricultural fields. Since most air pollutant chemicals can absorb infrared light, we are able to detect them with an infrared spectrometer. Some of the molecules commonly found in the atmosphere include those in Table 3.1. Water and small amounts of carbon dioxide, methane, and sulfur trioxide are found in “clean” air samples. Large amounts of any of the chemicals other than water usually indicate atmospheric pollution.
| Chemical Name | Chemical Formula | Description |
|---|---|---|
| Water | H2O | Ubiquitous in the atmosphere, even on dry days. |
| Carbon Dioxide | CO2 | Produced by the combustion of fuels (including the food we eat) and is a major source of greenhouse warming in the atmosphere. |
| Methyl halides | CH3X | Used as pesticides that are sprayed on agricultural fields. They currently are under strict EPA controls and are partially responsible for the ozone hole. |
| Dichlorodifluoromethane | CCl2F2 | refrigerant that is partially responsible for the ozone hole. |
| Ethylene | C2H4 | A component of natural gas. Is used to ripen bananas. |
| Acetylene | C2H2 | Fuel for high-temperature torches. |
| Sulfur trioxide | SO3 | Originates from the burning of sulfur-containing fuels such as coal. Reacts with water to form acid rain. |
| Benzene | C6H6 | A component of gasoline; is carcinogenic. |
| Dichloroethylenes (DCE) | C2H2Cl2 | Used in the dry-cleaning and polymer industries. |
| Percholoethylene (PCE) | C2Cl4 | Used in the dry-cleaning and polymer industries. |
| Hydrogen Peroxide | HOOH | A component of smog. |
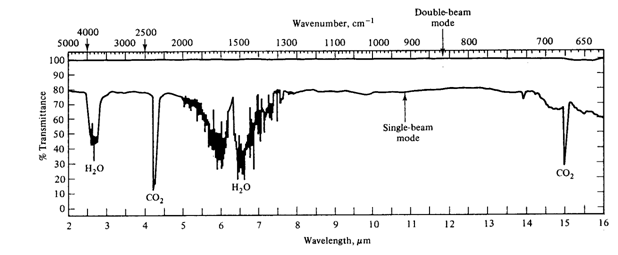
When testing, a test sample is first obtained by taking an evacuated cell to the target location, opening a valve, and allowing the ambient air to fill the cell. An FTIR – Fourier Transform Infrared Spectrometer will be used to perform Infrared Spectrometry. The final output from the spectrometer called an infrared spectrum (Figure 3.1), is a plot of the intensity of light reaching the detector divided by the initial intensity of light, as a function of frequency (%Transmittance= I/Io vs. frequency). The goal of this project is to gain a better understanding of group theory and to identify atmospheric pollutants from their infrared spectra.
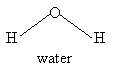
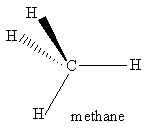
For the molecules listen in Table 4.1, examine the three-dimensional ball-and-stick models for these molecules and compare them with the two-dimensional representations of the molecules in Figure 3.2. In the drawings in Figure 3.2, straight lines represent bonds that lie in the plane of the paper; two lines between a pair of atoms represent a double bond; a filled arrowhead indicates a single bond that is angled out of the plane of the paper toward you; and the dashed arrowhead indicates a bond angled into the plane of the paper away from you. Carbon dioxide is an example of a linear molecule; water, ethylene, sulfur trioxide, and benzene are planar molecules.
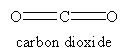
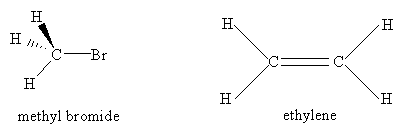

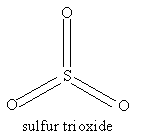


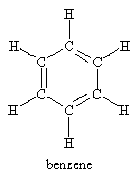
Problem #1: Center-of-mass and Coordinate Axes
In order to accomplish our goal of identifying the chemical pollutant you are investigating from its infrared spectrum, we must know which infrared frequencies, if any, the molecule absorbs. To decide which molecules absorb infrared radiation and at which frequencies, we will need to examine various properties of the molecules themselves, including their centers of mass, their Cartesian coordinate axes, their vibrations, and their symmetries. Specifically, we will compare the actions of the symmetry operations of a molecule on its Cartesian coordinate axes with the actions of the symmetry operations on its vibrations.
When a molecule absorbs infrared radiation of a given frequency, this energy causes the molecule to vibrate in a specific way; the atoms bounce against each other much like balls connected by a spring. The vibrational motions of a molecule that absorb infrared radiation are the ones that exhibit the same behavior as do the Cartesian coordinate axes of the molecule when the atoms of the molecule are permuted in certain ways. This is a result of the orthogonal interaction between the electromagnetic field of the light and the electric field of the molecule itself. Therefore, you will begin by drawing in a three-dimensional coordinate system for each of the molecules in the set assigned (see Table 3.2). The convention for molecules is that the origin of the axis system is placed at the center of mass of the molecule. (This is the weighted average of the positions of the atoms.) First, determine approximately where this should be. (You might want to reexamine the ball-and-stick models.) Remember, the masses of the different atoms are different. To find out how much each atom weighs; consult a periodic table of the elements. The mass number for each type of atom appears at the bottom of the square in which the atomic symbol appears.
By convention, the z-axis is the unique axis, if there is one. This axis is also called the molecular axis, or axis of highest symmetry. In a linear molecule, it corresponds to the line formed by the molecule; this is true for carbon dioxide. For benzene, the z-axis is the out-of-plane axis since it is the unique axis. If there doesn’t seem to be a unique axis, then place the heaviest atoms in the molecule along the z-axis (often, there is more than one way to do this). Once the z-axis is assigned, the in-plane axis usually is the y-axis and the out-of-plane axis is the x-axis. In addition, axes should be placed along the molecular bonds whenever possible.
The y- and z-axes for water and carbon dioxide are shown in Figure 3.3. The x-axis is out-of-plane from the origin (just below the O atom and pointing straight out at you for water, but centered in the C atom and pointing directly away from you for carbon dioxide).
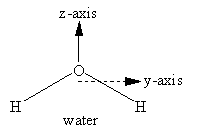

Assignment
Draw in the three Cartesian coordinate axes in a picture of each molecule assigned to you in Table 3.2 as outlined in the steps below. (If you do not assign them correctly now, you will have a chance later to re-label them.)
- Estimate, by eye, the center of mass for each molecule, keeping in mind the atomic masses for each type of atom.
- Draw in the z-axis using the rules above.
- Draw in the two remaining axes using the rules above.
| Group Letter | Assigned Molecules |
|---|---|
| A and E | dichlorodifluoromethane, hydrogen peroxide, nitrous oxide, sulfur trioxide |
| B and F | trans-1,2-dichloroethylene, ethylene, nitrous oxide, methyl bromide |
| C and G | gem-1,1-dichlorethylene, dinitrogen tetroxide, nitrous oxide, ammonia |
| D and H | cis-1,2-dichloroethylene, perchloroethylene, nitrous oxide, methyl iodide |
Problem #2: Molecular Vibrations
The types of molecular vibrations a molecule has determine whether or not it absorbs infrared light. Hence, you need to determine the types of vibrations your molecules make. To ensure that all of them have been identified, we need to know how many are possible. Consider a molecule that is a collection of N atoms connected together in a specific way by chemical bonds. In order to describe the motions of the molecule, we need to consider the motions of each individual atom. This means that we need 3 degrees of freedom for every atom within the molecule for a total of 3N degrees of freedom. However, the atoms within the molecule have a specific geometric relationship to the other atoms in the molecule; this results in a redistribution of the number of independent degrees of freedom. The motion through space of the molecule uses three degrees of freedom, reducing the 3N degrees of freedom to 3N - 3. Since the molecule also can rotate (like a spinning baton or Frisbee), we require two degrees of freedom to describe the coordinates about which a linear molecule can spin and three degrees of freedom for a non-linear molecule (for a linear molecule there is no concerted rotation about the molecular axis (z-axis). This leaves 3N - 5 degrees of freedom for the linear molecule and 3N - 6 for the non-linear molecule still unaccounted for; each of the remaining degrees of freedom describes a distinct coordinated internal motion, or vibration, of the atoms within the molecule.
For example, when there are only two atoms in the molecule (e.g. O2, N2, or CO), there is only one vibrational motion: 3(2) - 5 = 1. In the case of benzene (C6H6) there are 12 atoms and 3(12) - 6 = 30 vibrational motions possible! As it turns out, not all of these vibrations are capable of absorbing infrared radiation. For the simplest molecules, such as water, it is easy to draw pictures representing the vibrational motions.
Water has 3(3)-6=3 vibrations and carbon dioxide has 3(3)-5=4 vibrations as shown in Figures 3.4 and 3.5.
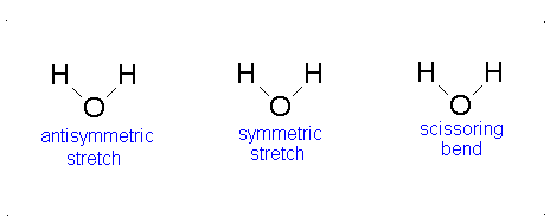
Consider the water molecule as it undergoes the asymmetric stretch; as it reaches its most extreme position, it has one “arm” extended and the other “arm” contracted. The bend is a change largely in angle and not inter-atom distances.
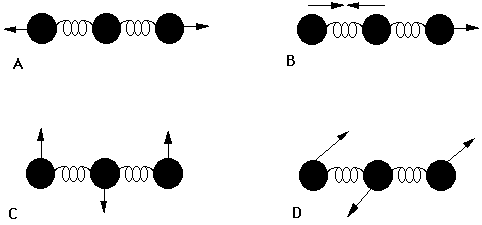
The four vibrations for CO2 consist of two stretches (one symmetric and one asymmetric) and two bends, that are degenerate (with the same energy) but involve perpendicular motions.
Assignment
For each molecule, calculate the number of vibrational motions using the formula given above. Then, use a computer program to view the vibrational motions for water, carbon dioxide and the other molecules assigned. Record the motions of the atoms in the molecule using the symbols from the examples above, and record the frequency calculated for each vibration. Note that some of these motions are out-of-plane motions. Be sure to rotate the molecules on the computer screen so that you examine the motions from many different angles. (Many of the programs calculate the frequencies in cm-1; this is actually the frequency, in s-1, divided by the speed of light (3.00 x 1010 cm/s). In this exercise, make note of the frequencies in cm-1 given by the HyperChem program.) Again, you are to complete the following steps for the molecules assigned to you in Table 3.2. This assignment will require a lot of space in your lab notebook due to all of the vibrations you will be drawing.
- Determine the number of vibrational motions, 3N – 6 or 3N – 5, to make sure that you know how many vibrational motions to record.
- Record the vibrational motions for your molecules, following the notation used in the examples above.
- Record the frequency for each of these vibrations.
- Double-click “PC Spartan '16” on desktop. The Spartan computer is located in the TA area of 3475 and has a bright orange name tag.
- Click the new page icon in the top left corner. Atoms with various bond choices will appear. If you prefer a more advanced setting, click the Expert tab.
- Draw your molecule by clicking on the atom with the correct number of bonds needed. To join two atoms, repeat this process by touching the mouse arrow to the open bond.
- Once you are done drawing your molecule, click the Glasses ("View") icon located just below the Geometry scroll-down. This will finalize your drawing.
- Next, go to the Setup scroll-down and select Calculations. The following will be your entries:
- Calculate: Equilibrium Geometry with Hartree-Fock 3-21G(*)
- Compute: IR
- Print: Vibrational Modes
- Go to Setup and scroll down to Submit. Make a new folder with your group's letter in the Chem 115 folder. Label within your folder as you see fit.
- After you save the file you will be prompted twice that Spartan has started and completed. Press OK both times.
- Go to Display and scroll to Spectra. Here you will find the frequencies associated with the different vibrations of your molecule. Click on any of the checkboxes to view the animation for the vibration associated with that particular frequency.
Problem #3: Symmetry Elements and Symmetry Operations
Because the molecules we are examining are very small, the rules of quantum mechanics govern the processes in which we are interested in. According to quantum mechanics, not all light absorption processes are allowed; many are “forbidden” by symmetry. If we want to determine which molecular vibrations absorb infrared light, we need to examine the actions of the symmetries of the molecules on the coordinate axes and on the molecular vibrations. We begin by determining the symmetry elements that each molecule possesses.
A symmetry operation on a molecule is an action that moves the molecule into a position that is indistinguishable from the starting position. A symmetry element of a molecule is a geometric feature of the molecule about which a symmetry operation is performed. Symmetry elements include planes and axes; symmetry operations include reflections across planes and rotations about axes. In the case of water, 180° rotation about the z-axis is a symmetry operation, denoted C2; while the z-axis itself is a symmetry element, a C2 axis. The symbol C3 indicates a three-fold axis of symmetry, a symmetry element; while C3 indicates a 120°rotation about a C3 axis, a symmetry operation. Rotation by 240° about a C3 axis is denoted C32. Rotation by 360° about a C3 axis is equivalent to doing nothing; that is, C33=Ê, where Ê is the identity operation.
| Symmetry Element | Symmetry Operation | ||
|---|---|---|---|
| Symbol | Description | Symbol | Description |
| \(E\) | Identity | \(\hat{E}\) | No change |
| \(C_{n}\) | n-fold axis of symmetry | \(\hat{C}_{n}\) | Rotation about the axis by 360°/n |
| \(\sigma\) | Plane of symmetry | \(\hat{\sigma}\) | Reflection through the plane |
| \(i\) | Center of Inversion | \(\hat{i}\) | Reflection through the center |
| \(S_{n}\) | n-fold rotation-reflection axis of symmetry, also called improper rotation axis | \(\hat{S}_{n}\) | Rotation about the axis by 360°/n followed by a reflection through a plane perpendicular to that axis |
The plane of symmetry, σ, is also referred to as a reflection plane or mirror plane. The symbol σv is used to denote a “vertical” plane of symmetry that is parallel to an axis of highest symmetry (z-axis, or Cn with largest n), while the symbol σh is used to denote a “horizontal” plane of symmetry that is perpendicular to the axis of highest symmetry (taken as z-axis). The symbol σd denotes a “dihedral” plane of symmetry that bisects an angle between atoms.
Figures 3.6 and 3.7 illustrate several of the symmetry elements listed in Table 3.3.
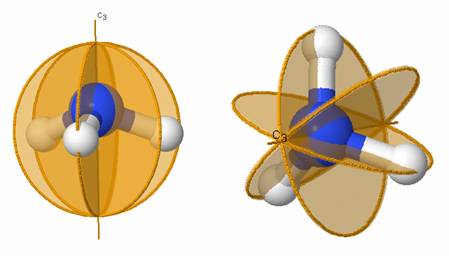
Figure 3.6: Symmetry elements for two views of ammonia (NH3). The C3 axis is labeled and the three mirror planes, σv, σv', σv'' are labeled as gold circles.
Figures 3.8 and 3.9 show the symmetry elements and operations of water and carbon dioxide, respectively.
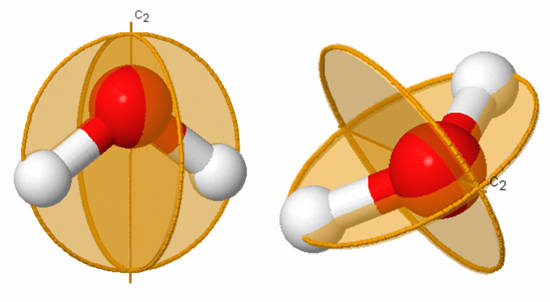
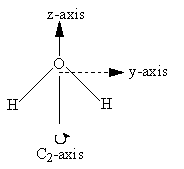
Figure 3.8: Symmetry elements of water viewed from differing perspectives
In the case of water the symmetry elements are E, C2 (shown), σv (xz-plane, perpendicular to the plane of the molecule), and σv’ (yz-plane, the plane of the molecule). Note that it does not matter whether σv represents the xz- or yz-plane. The corresponding symmetry operations for water are Ê, C2, σv, and σv’.
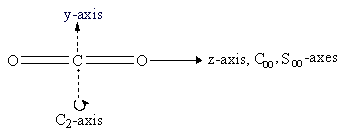
Figure 3.9: Symmetry elements of carbon dioxide
The symmetry elements not shown above are E, σv (yz-plane, the plane of the paper), σh (xy-plane, perpendicular to the C2 axis), and i (center of inversion at the coordinate origin). The symmetry operations for carbon dioxide are Ê, infinitely many C2, C∞, infinitely many σv, S∞, σh, and i. A subscript of ∞ means that rotation through any angle about that axis results in a valid symmetry operation. Note that σh is identical to S0 and is often omitted.
Assignment
Reexamine the ball-and-stick models for molecules assigned to you in Table 3.2. Determine all of the symmetry elements and corresponding symmetry operations for each molecule. (Hint: At least one molecule on the list contains the symmetry element σh and one contains an S3 symmetry element.)
There are a few things to keep in mind while trying to determine the symmetry elements for chemical compounds. The first is that molecules are three-dimensional objects. This means that we can tell the difference between the “front” and “back” or the “top” and “bottom” of planar molecules. For instance, the σv’ reflection of the water molecule across the yz-plane is not the same as the identity operation Ê. Second, since atoms of the same kind (or color) are indistinguishable, you may want to number the atoms in the models in order to keep track of the results of the symmetry operations. Finally, when molecules have hexagonal rings with alternating double bonds, all of these bonds---both single and double---are equivalent (e.g. benzene and toluene). It is only the orientation of the atoms themselves that can be “seen” spectroscopically and hence needs to be considered here.
After you have determined the symmetries of the molecules, you can double-check your axis assignments. The z-axis should be the axis of highest Cn symmetry. In H2O, there is only one Cn axis, C2, so it is the z-axis. In CO2, there is a C2 axis and a C∞ axis, so the C∞ axis is the z-axis. Check the other molecules to make sure that the z-axis you assigned is the one of highest symmetry. Remember that the axis of highest symmetry may not be unique.
Problem #4: Orders of Symmetry Operations
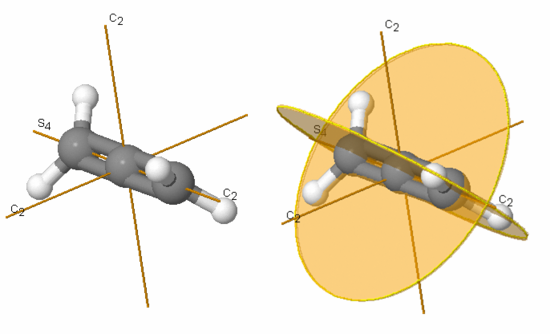
The order of a symmetry operation is the number of times the operation must be applied to obtain the identity operation, Ê. More specifically, the order of a symmetry operation  is n, if n is the smallest positive integer such that Ân = Ê. For instance, for H2O, the non-identity symmetry operations each have order 2. Note that an inversion always has order 2. The symmetry operation S4 has order 4 because it must be applied four times in succession to return the molecule to its original orientation when the outside atoms are labeled. (Try it for methane!) Therefore, S4 generates 4 symmetry operations: S4, S42 = C2, S43, and S44 = Ê of orders 4, 2, 4, and 1, respectively.
Assignment
For each of the molecules assigned to you in Table 3.2, find the order of each symmetry operation. Use the description of order to aid you.
Problem #5: Symmetry Groups
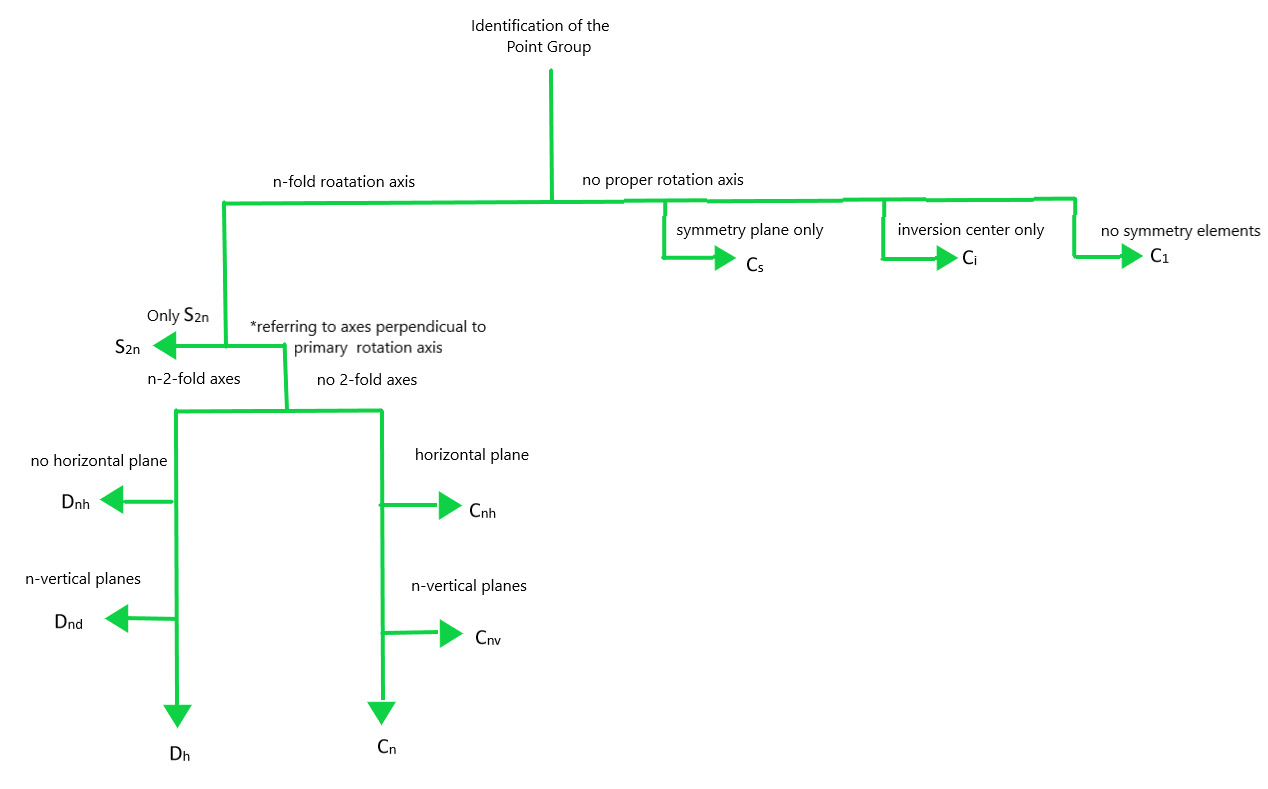
You may have noticed that the set of symmetry operations forms a group under composition of operations, called the symmetry group of the molecule. The symmetry elements of a molecule can be used to determine the group to which the molecule belongs. Using Figure 3.10 and the molecule's symmetry elements, the group can be identified.
Assignment
Identify the symmetry group for each of the molecules assigned to you in Table 3.2. The order of a symmetry group is the number of operations which comprise the group. What is the order of each group? Verify by determining the group for your molecules from HyperChem and by examining the character tables in Chapter 12 of McQuarrie and Simon (Chem 110B text) or Chemical Applications of Group Theory, by F. A. Cotton. There are also tutorials available on to help identify the group and practice finding groups of other molecules.
Problem #6: Action of Symmetries on Coordinate Axes
Your overall goal is to identify the molecular origins of the infrared peaks observed in a spectrum of contaminated air. Since a molecule’s infrared light absorption depends on how the Cartesian axes transform under the symmetry operations, the next step is to determine what happens to each of the Cartesian axes as the different symmetry operations are performed upon the molecule.
In Figure 3.11 and Table 3.4, we illustrate this process for water. Note that under the identity operation, Ê, none of the axes are inverted or reversed. When the molecule is rotated about the C2 axis, the orientation of the z-axis remains the same but the x- and y-axes are oriented in the opposite direction; each point (x,y,z) is moved to the point (-x,-y,z). In this case, the rotation is equivalent to multiplying the x and y values by -1. For any operation, -1 indicates that there is a reversal in the orientation of the axis relative to the original orientation, whereas +1 indicates that the orientation remains the same.
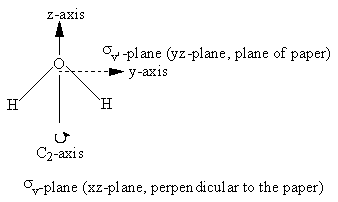
Figure 3.11: The coordinate axes and symmetry elements for water
| H2O | Ê | C2 | σv (xz) | σv’ (yz) |
|---|---|---|---|---|
| X | 1 | -1 | 1 | -1 |
| Y | 1 | -1 | -1 | 1 |
| Z | 1 | 1 | 1 | 1 |
Assignment
Construct similar tables for the FIRST THREE molecules assigned to you in Table 3.2. First, check with your TA to make sure you have drawn the Cartesian coordinate axes in the standard way for each of these molecules.
Problem #7: Action of Symmetries on Vibrational Motions
The vibrational motions of the molecule that absorb infrared radiation are the ones that transform under the symmetry operations of the molecule in the same way as do the Cartesian coordinate axes of the molecule. Therefore, we need to determine how the molecular vibrations behave under each of the symmetry operations, so that we can compare them to the transformations of the Cartesian coordinate axes.
Let us examine the vibrations of water again (Figure 3.12).
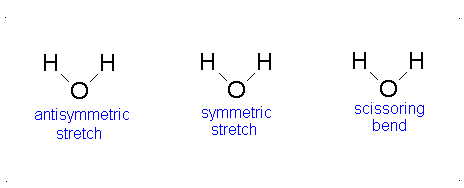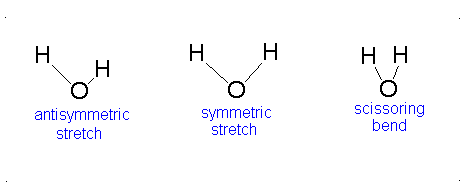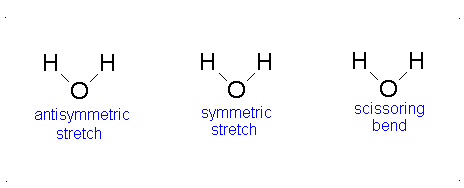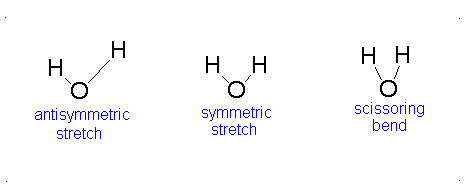
Figure 3.12: Vibrations of water
If we ask how each of the vibrations of water behaves under each of the symmetry operations, we can add more entries to Table 3.5. When we examine what happens to the vibrating molecules as the symmetry operations are performed, we are interested only in whether or not the geometrical orientation of the molecule has changed. For instance, consider the water molecule as it undergoes the asymmetric stretch. Imagine the molecule (or stop the computer program) when it reaches its most extreme position, with one “arm” extended and the other “arm” contracted. Now perform the C2 operation (rotation by 180°) on this “distorted” molecule. Its orientation after the C2 operation is different from its orientation before. Note that the configuration has been reversed. The fact that its new position is distinguishable from its original position is represented in Table 3 by -1.
Now let’s examine the water molecule as it undergoes the bend or symmetric stretch. If we perform the C2 operation (rotation by 180°) on this vibrating molecule, its geometric orientation is unchanged. Its new position is indistinguishable from its original position. The fact that it appears unchanged is represented in Table 3.5 by +1.
| H2O | Ê | C2 | σv (xz) | σv’ (yz) |
|---|---|---|---|---|
| X | 1 | -1 | 1 | -1 |
| Y | 1 | -1 | -1 | 1 |
| Z | 1 | 1 | 1 | 1 |
| bend | 1 | 1 | 1 | 1 |
| symmetric stretch | 1 | 1 | 1 | 1 |
| asymmetric stretch | 1 | -1 | -1 | 1 |
Assignment
Construct tables as in example 3.6 for the FIRST THREE molecules assigned to you in Table 3.2. Examine the motions of the atoms for each different vibration. If you were to imagine the molecule (or stop the computer program) when it reaches its most extreme position, consider how that “version” of the molecular shape would behave under each of the different symmetry operations. That the molecule is indistinguishable after the symmetry operation is indicated by a 1, while a distinguishable molecule is represented by a -1. Fill in a line in your table for each vibrational motion. Note this procedure works for most, but not all simple molecules. For example, this procedure will not work for your third molecule.
Problem #8: Comparing Symmetry Operations on Axes and Vibrations
When a symmetry operation and an axis transform in the same way, the frequency associated with that symmetry operation will absorb light. By comparing the tables you generated in
In the case of water, as illustrated in Table 3.5, the bending vibration transforms under the symmetry operations in the same way as does the z-axis. This is also true for the symmetric stretching motion. On the other hand, the asymmetric stretch transforms in the same way as does the y-axis. In this case, all three of the vibrational motions of water would absorb infrared light since each one of them transforms under the symmetry operations as does one of the Cartesian coordinate axes. All of the vibrations also have frequencies that are in the appropriate frequency range. We would expect the infrared spectrum of water to have three peaks corresponding to frequencies of 1840, 3587, and 3652 cm-1.
Assignment
For the FIRST THREE molecules assigned to you in Table 3.2, use the tables you constructed in Problem #7 to determine how the vibrational motions transform under the symmetry operations. List the frequency calculated of the ones that transform as do the x-, y-, or z-axes. (You listed the frequencies you need for this problem in Problem #2.) Given that infrared spectrometers operate in the range of about 600 cm-1 to 4000 cm-1 (wavenumbers), which vibrational frequencies should you observe in the infrared spectra for your molecules? Make a rough sketch of the infrared spectrum you would expect to see for each of your molecules, labeling peaks with their frequencies. Assume that if peaks are separated by less than 25 cm-1, they will not be resolved and will appear as a single peak.
Problem #9: Obtaining Infrared Spectra
You have now reached the experimental portion of this exercise. Before you can measure your contaminated air sample. You will need to measure some common air pollutants. The IR spectra that you measure for these molecules will help you decide which compound is in your air sample.
Assignment
Breathing into the sample compartment of the infrared spectrometer can generate the spectrum of water and carbon dioxide. You will then take spectra of methyl iodide, ethylene, acetylene, trans-DCE, and a sample of contaminated air, which have already been prepared in infrared cells. Do not be overly concerned if the windows on the cells appear to be hazy; they will work fine. Do you observe the predicted absorptions? If not, try multiplying all of your vibrational frequencies by 0.89 (a factor theoretical chemists recommend to compensate for over calculations). Do they come closer to what you observe now?
- Start the OPUS 6.0 software on the computer next to the instrument.
- In the Measure Menu, go to the Advance tab to set the parameters for the experiment
- Scans: 16 for sample and 16 for background
- Resolution: 2.0
- Signal Gain: 1
- IR Data Type: Transmittance
- Go to Path: and select the Chem115 directory for data storage
- Name your sample in the Filename: field
- Close the sample compartment and wait 2-3 minutes for the sample compartment to be purged of air.
- In the Measure Menu, go to the Basic tab. Click the “Background Single Channel” button, the instrument will start scanning the background. The progress status will be shown at the bottom of the screen.
- Open the chamber, and load your sample in. Close the chamber.
- To acquire your sample scan. Give your sample a description under the Basic tab. Run the sample spectrum by clicking on the “Sample Single Channel” button. The progress of the scan can be seen at the bottom of the screen.
- Start the OPUS 7.2 software on the computer next to the instrument.
- In the Toolbar Menu, find the Advance Measurement tab to set the parameters for the experiment

- Scans: 16 for sample and 16 for background
- Resolution: 2.0
- Signal Gain: auto
- IR Data Type: Transmittance
- Go to Path: and select the Chem115 directory for data storage
- Name your sample in the Filename: field
- Close the sample compartment and wait 2-3 minutes for the sample compartment to be purged of air.
- In the Measure Menu, go to the Basic tab. Click the “Background Single Channel” button, the instrument will start scanning the background. The progress status will be shown at the bottom of the screen.
- Open the chamber, and load your sample in. Close the chamber.
- To acquire your sample scan. Give your sample a description under the Basic tab. Run the sample spectrum by clicking on the “Sample Single Channel” button. The progress of the scan can be seen at the bottom of the screen.
2022-Agilent's modular Cary 630 FTIR will be used with stainless steel gas cells, ask your TA, Paul or his staff.
Collect a spectrum of water and carbon dioxide:
- Launch MicrolabPC on the laptop connected to the Cary 630. user:Admin/pswd: 3000hanover. Yes, make changes. Enter pswd again.
- Ensure the transmission module is pictured and all indicators are GREEN.
- Click start to check the crystal and prepare for background scanning. Click next to acquire the background.
- Prepare Sample: on the next screen enter sample ID or comments and without clicking next; open the compartment of the transmission module and exhale into it.
- You will observe the the live signal. Clicking next will collect the data and display the FTIR spectum.
- Pick peaks for frequency labeling by clicking on the white area outside and to the right side of the spectral window and inside the grey area of MicroLab.
- Tap and drag to label the peaks desired. Clicking Data Handling and Print Report will provide a .pdf for hardcopy or to export as electronic data.
Collect spectra of the four reference samples and your unknown:
- Follow the above procedure for Cary 630. Open the sample compartment and fan the lid to refresh the background.
- Some methods store the background for 20 minutes, others take the background for each sample.
- Insert cells inside the cell holder by aligning the cylinder ridges with module's alignment grooves and ensure the ID tag is not caught in between. Gently lower the cell.
- Make sure you name the file before clicking next.
- A second unknown sample may be available for Bonus Points, ask your TA or Paul.
To pick peaks: (This procedure may not work depending on the instrument you are using.)
Click on the peak picking icon, or select Peak Picking from the Evaluate menu. Cary 630 peak picking is above.
- The peak picking screen will show up. Choose the Interactive mode. Sliding the Threshold square up or down so that all the peaks are below it.
- Each peak above the threshold will be labeled with its frequency and the peak list will be written to a report file that you must save by selecting Save Report from the File pulldown menu.
- You can annotate the plot by selecting the annotator options from the Tools pulldown menu.
- The file path and name are the default title for your plot. You can change this by selecting Title under the Display pulldown menu.
- Once you have picked your peaks and annotated your plot, save the window as before by selecting Save Sample from the File pulldown menu.
- Select Plot from the File pulldown menu. In the Plot menu select the window you wish to print. Check that the size of the plot is correct and then click on the “plot”. This will take 1-2 minutes. Be patient. You can then select another window to print or click on the “done” button.
Problem #10: Identifying the Pollutant
As a reminder: The sample was taken in a location 20 m away from an open farm field where strawberries were growing. In the field on one side, there were cows grazing; on the other side, there was a natural gas pumping station. Across the street, there was a gas station with an auto repair shop specializing in air conditioner repair and a dry cleaner. This information narrows the list of suspected chemicals to six. Test your air sample and determine the culprit. The spectrometer automatically purges the cell cavity with N2, which is transparent in infrared. This removes water and carbon dioxide, which exhibit strong IR absorptions, so you should be able to see the pollutant's spectrum relatively easily.
Assignment
Examine the spectrum from your sample of the unknown, contaminated air. Note that it is a very different spectrum from that of carbon dioxide and water, which is shown in Figure 3.1. Which of the chemicals that you studied is responsible for this spectrum? To which potential polluter described above would you attribute this pollution?
Post-Lab Questions
1. Include all of the information recorded during the assignments.
2. Include all of the FTIR spectra
3. Identify the pollutant and predict the source of the pollutant.
4. Explain the process used to identify the pollutant.
References
- McQuarrie, D. A.; Simon, J. D. Physical Chemistry: A Molecular Approach; University Science Books: Sausalito, CA, 1997.
- Cotton, F. A. Chemical Applications of Group Theory; Wiley: New York, NY, 1990.
- Drago, R. S. Physical Methods in Chemistry; W. B. Saunders: Philadelphia, PA, 1977.
- Skoog, D. A.; Holler, F. J.; Crouch, S. R. Principles of Instrumental Analysis, Seventh Edition; Cengage Learning: Boston, MA, 2016.
Contributors and Attributions
- Dr. Christopher Brazier, Dr. Steven Morics, Dr. Teresa Longin, Dr. Dara Gilbert, Dr. David Goodin, and Brooke McMahon


