3: Analysis of key experiments revealing the structure of the atoms
- Page ID
- 16969
J.J. Thomson's experiment and the charge-to-mass ratio of the electron
The first is the experiment of Joseph John Thomson, who first demonstrated that atoms are actually composed of aggregates of charged particles. Prior to his work, it was believed that atoms were the fundamental building blocks of matter. The first evidence contrary to this notion came when people began studying the properties of atoms in large electric fields.
If a gas sample is introduced into the region between two charged plates, a current flow can be observed, suggesting that the atoms have been broken down into charged constituents. The source of these charged particles is a heated cathode that, in fact, causes the atoms of the sample to ionize. These were known as cathode rays. In 1897, Thomson set out to prove that the cathode rays produced from the cathode were actually a stream of negatively charged particles called electrons. From Maxwell's theory, he knew that charged particles could be deflected in a magnetic field. A schematic of the experimental setup is shown below:
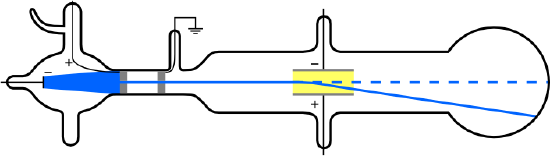
1: Schematic of J.J. Thomson's experiment.
We now zero in on the field region and set up a coordinate system as shown in the figure below:
![\includegraphics[scale=0.6]{lec3_fig1.eps}](http://www.nyu.edu/classes/tuckerman/adv.chem/lectures/lecture_3/img2.png) |
In this coordinate system, electrons enter the region between the plates with an (unknown) velocity \(v\) in the \(x\)-direction. In order to determine this velocity, electric and magnetic fields are both applied, and each gives rise to a force on the electron. These forces are in the \(y\)-direction. The electric force \(F_E=eE\), where \(E\) is the magnitude of the electric field, and the magnetic force is \(F_H=-evH\), where \(H\) is the magnitude of the magnetic field, and is opposed to the force on the electric field.
If these forces balance, then there will be no deflection of the electron in the \(y\)-direction, i.e. all of the electrons' motion will be along the ![]() \(x\)-direction, which was the initial direction when they entered the field region. If the forces balance, then the total force on the electrons will be zero, that is \(F_E +F_H=0\) or
\(x\)-direction, which was the initial direction when they entered the field region. If the forces balance, then the total force on the electrons will be zero, that is \(F_E +F_H=0\) or
from which the unknown velocity can be determined as
Next, the magnetic field is switched off, so that the total force is due entirely to the electric field. Since the force is non-zero, if the charge carriers can be deflected by the force, this provides evidence for their being fundamental particles. If they are fundamental charged particles, then they should have a well defined mass and charge. In this second part of the experiment, the specific trajectory followed by the particle will be used to determine the ratio of the charge to the mass of the particle.
When there is only an electric field, then there is a nonzero force \(F_E =eE\) in the \(y\)-direction but no force in the \(x\)-direction. Thus, this problem is exactly the same as that of a projectile in a gravitational field. As can be done in the projectile problem, the \(x\) and \(y\) motion of the electrons can be analyzed separately and independently.
In the \(x\)-direction, the motion is very simple because there is no force in this direction. The electrons simply move with a constant velocity \(v\), which we already determined has the value \(E/H\). Note that this value is correct even though there is no magnetic in this part of the experiment! It is just the velocity we determined from the previous part of the experiment, and this value has not changed. Thus, as a function of time \(t\), the \(x\)-position of the electrons is
\[x(t)=vt=\dfrac{E}{H}t\]
The force in the \(y\)-direction is a constant, hence motion in the \(y\)-direction is analogous the gravitational force. The constant force \(F_E\) gives rise to an acceleration \(a=F_E /m\), and the \(y\)-position at time \(t\) is then
The electric field is tuned such that the particle traverses the entire plate region in the time required for it to strike the positive plate. Let the total \(y\) distance travelled be ![]() \(s\), as shown in the figure. The time \(T\) required to traverse the plate region \((x(T)=l)\) is
\(s\), as shown in the figure. The time \(T\) required to traverse the plate region \((x(T)=l)\) is
\[l=\dfrac{E}{H}T\]
\[T=\dfrac{lH}{E}\]
This is also the time required to move a distance \(s\) in the \(y\) direction:
Solving the above for the ration \(e/m\) gives
Thus, using his experimental apparatus, Thomson was able to determine the charge-to-mass ratio of the electron. Today, the accepted value of \(e/m\) is \(1.7588196*10^{11} C/kg\).
In 1906, Robert Millikan was able to determine the value of the charge on the electron in his ``oil drop'' experiment. A schematic of his experiment is shown below:
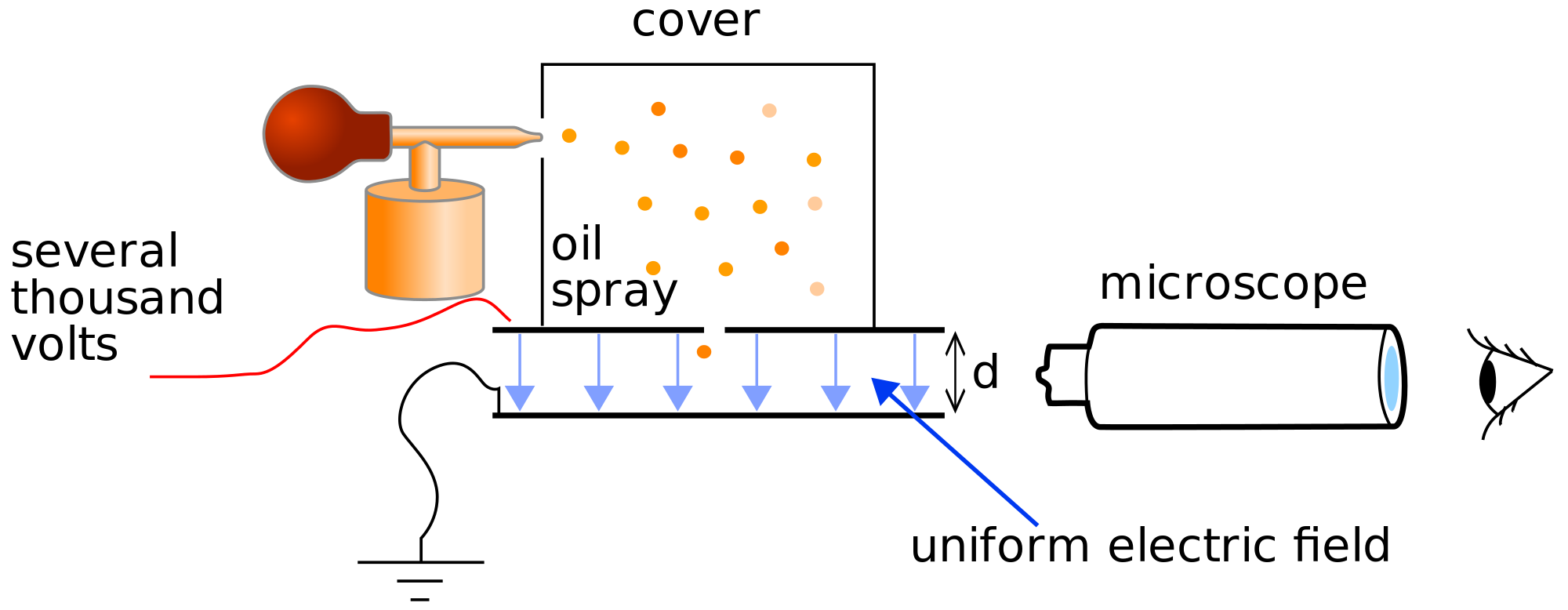
Then using Thomson's value of \(e/m\), he calculated the value of \(m\). In his experiment, Millikan used a fine spray of ionized oil droplets, which he allowed to be acted on by gravity but to which he also applied an electric field in the direction opposite gravity, i.e. up. By tuning the electric field, he balanced the force due to the pull of gravity and the electric field force so that the drops remained suspended in space. Thus, if a drop has a positive charge \(q\) and a mass \(M\), the force balance condition becomes
where \(E\) is the magnitude of the electric field. Solving for the charge-to-mass ratio, we have \(q/M=g/E\). In order to determine the mass, the drops are allowed to fall in the gravitational field without the influence of the electric field. In this case, there are still two forces acting on the drops. One is the gravitational force and the other is the frictional force due to air resistance. Since this force is proportional to the velocity, it vanishes when the drop is stationary, which is why it does not need to be taken into account when the electric field is on. However, when the drops are allowed to fall, the total force is \(F=Mg-\gamma v\), since friction opposes gravitational force. Here, \(\gamma\) is the coefficient of air resistance. Thus, according to Newton's law of motion
\[Ma=F\]
\[M\dfrac{dv}{dt}=Mg-\gamma v\]
Assuming the drop starts initially at rest, the equation can be solved for \(v(t)\), yielding
Since \(M\) is very small and \(\gamma\) is relatively large, the exponential factor quickly decays to 0, leaving simply a constant velocity \(v=Mg/\gamma\) known as the terminal velocity. This velocity can be measured and used to solve for the mass \(M\). Once the mass is known, the charge-to-mass ratio determined above can be used to determine the charge \(q\). The last remaining technical problem is that it is not known how many electrons are stripped off each drop before the experiment is performed. Thus, each drop will have a different charge \(q\) that is a multiple of the fundamental charge unit \(e\). By subtracting successive values of \(q\) obtained for different drops, however, it is possible to find a ``smallest'' value, which can be assumed to be a prediction of \(e\), although the possibility that the result is still a multiple of \(e\) cannot be ruled out.
The currently accepted values of \(e\) and \(m\) are:
\[e=1.6021773*10^{-19} \ C\]
\[m=9.109390*10^{-31} \ kg\]
Rutherford's experiment and the nature of the atomic nucleus
The nature of the atomic nucleus was first elucidated experimentally by Ernest Rutherford in 1911. He observed the scattering of \(\alpha\)-particles (helium nuclei) from a thin gold foil (see schematic below):
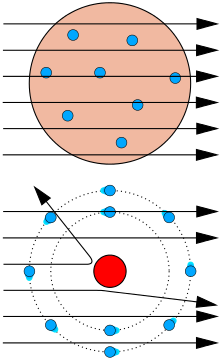
As he had assumed a relatively uniform mass distribution throughout the gold foil, he was surprised to observe that most of the \(\alpha\)-particles passed through the foil essentially undeflected, as if through empty space. Occasionally, an \(\alpha\)-particle would be scattered strongly, as if it had collided with a dense concentration of mass. He, thus, concluded that most of the mass of the gold atoms was concentrated in a tiny, dense kernel that he called the nucleus.
Rutherford estimated the ``diameter'' of an atom to be approximately \(10^{-8} \ cm\) and that of the nucleus to be approximately \(10^{-13} \ cm\). He proposed a model of the atom as consisting of a small, dense nucleus surrounded by enough electrons to yield an overall charge-neutral aggregate. That is, if the nuclear charge is \(+Ze\), then the atom must possess \(Z\) electrons. The model later introduced by Bohr, and even the current quantum mechanical picture of the atom (which you will see next semester), were built upon Rutherford's original model.
As mentioned in the first lecture, we know today that the atomic nucleus is composed of protons and neutrons. If a nucleus has \(Z\) protons and \(N\) neutrons, it is said to have a mass number \(A\) equal to \(Z+N\). Thus, if \(X\) represents the chemical symbol of some element, then its nucleus is represented by
\[_{Z}^{A} X\]
Nuclei of the same chemical species having different mass numbers, hence different numbers of neutrons, are called isotopes of that species. Thus,
\[_{Z}^{A} X \ and \ _{Z}^{A'} X\]
are isotopes of the element \(X\). For example,
\[_{1}^{1} H, \ _{1}^{2} H, \ and \ _{1}^{3} H\]
are isotopes in the hydrogen family, called ``hydrogen,'' ``deuterium,'' and ``tritium,'' respectively.
Expressing the mass of an atom
The mass of a hydrogen atom is \(1.6727*10^{-27} \ kg\). To avoid having to work with such small numbers all the time, the tradion of using a relative atomic mass scale was started. Although such a relative scale has undergone several incarnations, in 1961, by international agreement, a scale was settled upon.
A relative scale can be devised by assuming that one of the elements has exactly one mass unit for each of its nucleons. In 1961, it was decided that \(_{}^{12}C\) would be the element that defined the scale. Thus, the scale of relative atomic mass of \(_{}^{12}C\) is taken to be exactly \(12\) (and no units are assigned to this number). Then, the masses of all other elements are defined with respect to this scale. Thus, knowing the actual mass of a \(_{}^{12}C\) atom \((1.9927*10^{-26} \ kg)\), and the actual mass of a hydrogen atom, we can determine the relative mass of hydrogen on this scale from
\[\dfrac{mass \ of \ an \ atom \ of \ H}{mass \ of \ an \ atom \ of \ C}=\dfrac{relative \ mass \ of \ an \ atom \ of \ H}{relative \ mass \ of \ an \ atom \ of \ _{}^{12}C}\]
\[\dfrac{1.6727*10^{-27} \ kg}{1.9927*10^{-26} \ kg}=\dfrac{relative \ mass \ of \ H}{12}\]
\[relative \ mass \ of \ H=1.0073\]
A complete list of relative mass of atoms is given in the table in the inside back cover of the book.
Notice, however, that the number we computed above does not correspond to what is in the table under hydrogen. Since many elements have isotopes, it is customary to express the relative mass of an atom as an average over the different isotopes. Thus, is an element has isotopes \(_{}^{A_1}X\), \(_{}^{A_2}X\), \(_{}^{A_3}X\), ... with relative masses \(A_1\), \(A_2\), \(A_3\),... then the relative mass \(A\) associated with an atom of X is given by
where \(p_i\) is the fractional abundances of the \(i\)th isotope.
Example: \(_{}^{12}C\) and \(_{}^{13}C\) are stable isotopes of carbon with fractional abundances of \(98.934\%\) and \(1.0664\%\), respectively. The relative mass of \(_{}^{13}C\) is 13.003354. What is the average relative mass of carbon?
In order to establish a link between the mass of macroscopic amounts of matter that we ordinarily deal with and the masses of individual atoms, a connection exists through a number known as Avogadro's number \((N_0)\), which is defined to be the number of atoms in exactly \(12 \ g\) of carbon. The currently accepted value of \(N_0\) is \(6.0221420*10^{23}\). Then, the mass of any atom can be determined by dividing its relative mass \(A\) by \(N_0\):
For example, the mass of one atom of \(_{}^{12}C\) is
The mole concept
In everyday work, we deal with macroscopic amounts of substances. It is, therefore, useful to have a standard definition of macroscopic quantity of something. Avogadro's number is used to provide such a definition. We define \(1 \ mole\) of something to be the amount of that something which contains \(N_0\) individual entities of that thing. Thus, \(1 \ mole \ of \ sodium \ atoms=N_0\) sodium atoms. Now, if \(m_X\) is the mass of one atom of the element \(X\), then the mass of one mole of \(X\) is given by
\[m_X (g/atom) *N_0(atoms/mol)=m_X N_0(g/mol)\]
But \(m_X=A/N_0\). Thus, we see that the relative mass \(A\) also measures the mass of 1 mole of \(X\) (in g/mol, for example). For this reason, the relative mass \(A\) is also called the molar mass of \(X\), however to distinguish relative mass \(A\) from molar mass, we will use the symbol \(M\) for molar mass. Note, therefore, that \(12 \ g\) of \(_{}^{12}C\) is exactly \(1 \ mole \ of \ _{}^{12}C\), which explains why Avogadro's number is defined the way it is.Stoichiometry
Chemical Formulae
Molecules are aggregates of individual atoms held together by chemical bonds (to be discussed in the next chapter). Thus, a symbolic representation of a molecule should be composed of the chemical symbols for the individual atoms that comprise the molecule. There are two types of chemical formulae that are commonly used to represent a molecule:
- 1. Molecular Formula:
The molecular formula for a molecule expresses the precise number of each type of atom in that molecule.
Examples: \(CO_2\) is the formula for a molecule of carbon dioxide. \(H_2 O\) is the formula for a molecule of water. \(C_6 H_{12} O_6\) is the formula for molecule of glucose.
Note that the molecular formula is also the formula for the (bulk) substance, itself. That is, we say \(H_2 O\) is the molecular formula for water or ice, indicating bulk water or ice. This is true as long as the bulk substance has well defined molecular subunits.- 2. Empirical Formula:
The empirical formula is the simplest formula for a molecule that still expresses the correct relative numbers or ratios of numbers of atoms in the molecule.
Example: The numbers of carbon, hydrogen and oxygen atoms in glucose \((C_6 H_12 O_6)\) are in the ratio:- \[6:12:6\]
- \[1:2:1\]
Hence, the empirical formula for glucose is\[CH_2 O\]
Which contains more information?
Consider the empirical formula
This is a correct empirical formula for the following molecules:
- ethylene: \(C_2 H_4\)
- cyclopropane: \(C_3 H_6\)
- cyclobutane: \(C_4 H_8\)
- cyclohexane: \(C_6 H_{12}\)
or any other molecule for which the number of carbon atoms and the number of hydrogen atoms are in the ratio of \(1:2\). From this example, it is clear that the molecular formula carries more information and is clearly preferable to an empirical formula.
Put another way, an empirical formula specifies a class of molecules, in which the numbers of atoms are in certain basic ratios, while the molecular formula precisely identifies a particular molecule.
Although preferable, a molecular formula is not always possible. For example, in liquids and solids, it may not always be possible to define precise molecular units, in which case an empirical formula is the only possible choice.
Sometimes, enough information about a substance is given to determine the empirical formula only. Consider the following example:
Example 1
A \(10.0 \ g\) sample of a sand-like substance is known to contain \(46.01\%\) iron \((Fe)\) and \(53.99\%\) silicon \((Si)\) by mass. What is the formula for the substance?
Solution: The mass of \(Fe\) and \(Si\) in the sample can be determined from the given percentages:
\[mass \ of \ Fe=10.0 \ g*0.4601=4.601 \ g\]
\[mass \ of \ Si=10.0 \ g*0.5399=5.399 \ g\]
We convert masses to moles, since we want to know how many of each type of atom there is in the substance (expressed in moles), and hence how many of each type of atom in a molecule. This is done using the molar masses of each atom type.
\[moles \ of \ Fe = \dfrac{4.601 \ g}{55.847 \ g/mol}=0.08237 \ mol\]
\[moles \ of \ Si=\dfrac{5.399 \ g}{28.086 \ g/mol}=0.19223 \ mol\]
The ratio is:
\[0.08237:0.192234\]
\[1:\dfrac{7}{3}\]
\[3:7\]
So the formula, which is an empirical formula, is
The reason it is only an empirical formula is that if the true formula were \(Fe_6 Si_{14}\), the same percentages by mass would still hold.
Conservation of mass
Consider the balanced reaction from the previous lecture:
In this example, suppose \(2 \ mol \ of \ C_4 H_{10}\) are combined with \(13 \ mol \ of \ O_2\). What are the masses of the reactants and products?
Quantities in moles are converted to masses via the molar mass of each molecular species. The molar mass of a molecule is obtained by simply adding the molar masses of each of its atomic constituents. Thus, letting \(M\) be the symbol for molar mass,
\[M_{C_4 H_{10}}=4M_C +10M_H =4*12.011+10*1.0079=58.123 \ g/mol\]
\[M_{O_2}=2M_O =2.0*15.998=31.996 \ g/mol\]
\[M_{CO_2}=M_C +2M_O=12.011+2.0*15.998=44.007 \ g/mol\]
\[M_{H_2 O}=2M_H +M_O=2.0*1.0079+15.998=18.014 \ g/mol\]
Then, \(2 \ mol \ of \ C_4 H_{10}\) is equivalent to
etc. Thus, the chemical equation can be written as a statement about masses of reactants and products:
The total mass on the left side is \(116.25 \ g+415.95 \ g=532.2 \ g\), and the total mass on the right is \(352.0 \ g+180.14 \ g=532.2 \ g\). Thus, mass conservation is satisfied. The study of such mass relations in chemical reactions is called stoichiometry.
Limiting reagent
Chemical equations specify precise amounts of reactants that will combine to give products. In a real chemical reaction, arbitrary amounts of reactants are mixed together and allowed to form products, which means generally that one of the reactants will be used up completely, while excess amounts of other reactants will remain after the reaction has run to completion. The species that is fully consumed is called the limiting reagent. The limiting reagent will then determine what the yield of product will be.
When the quantities of reactants that are allowed to combine are specified, identifying the limiting reagent amounts to determining which of the reacting species yields the smallest amount of product.
Consider the following example.
Example 2
Sulfuric acid is produced in the reaction:
Suppose \(400 \ g \ of \ SO_2\), \(175 \ g \ of \ O_2\) and \(125 \ g \ of \ H_2 O\) are mixed and allows to react. Which reactant is the limiting reagent?
Solution: First convert the given masses to moles:
\[moles \ of \ SO_2 =\dfrac{400 \ g}{64.06 \ g/mol}=6.24 \ mol \ SO_2\]
\[moles \ of \ O_2 =\dfrac{175 \ g}{31.996 \ g/mol}=5.47 \ mol \ O_2\]
\[moles \ of \ H_2 O=\dfrac{125 \ g}{18.02 \ g/mol}=6.94 \ mol \ H_2 O\]
From the reaction equation, we see that
or
or
Similarly,
or
and
or
or
Since \(SO_2\) yields the smallest quantity of product, it is the limiting reagent.
Percentage yield
A balanced chemical equation tells what the theoretical or ideal yield of the reaction should be, assuming perfect completion of the reaction. In reality, the actual yield may be less than the theoretical yield. Reasons for this include:
- There may be competing reactions which hinder the process under consideration.
- External conditions may not be perfectly maintained.
- Reactants may not be pure.
The ratio of the actual yield to the theoretical yield is a quantity known as the fractional yield:
and the percentage yield is obtained from the fractional yield according to
Example
Pure zinc can be produced in the following two-step process:
\[2ZnS+3O_2 \rightarrow 2ZnO+2SO_2\]
\[ZnO+CO\rightarrow Zn+CO_2\]
Suppose \(5.32 \ kg \ of \ ZnS\) yield \(3.30 \ kg \ of \ pure\ zinc\). What is the percentage yield?
Solution: Convert the mass of \(ZnS\) to moles:
How do we figure out how many moles of \(Zn\) are produced in the two-step reaction? We need to obtain the overall reaction, which is just a ``sum'' of the individual steps. We can obtain the equation of the overall reaction by adding the equations for the individual steps. However, this addition must be carried out in a particular way. Specifically, note that the species \(ZnO\) is produced in the first step and consumed in the second step. Thus, it does not appear among the final products of the process, and for this reason, it is called an intermediate. The equations for the individual steps must be added in such a way that all intermediates cancel out. Since adding reaction equations works like the adding of algebraic equations, this means that the coefficients of intermediates must be the same in the individual steps. In the above process the coefficients of \(ZnO\) are different in each step. But, if the first step is divided by \(2\), so that the reaction equation reads:
then \(ZnO\) has the same coefficient in the first step as is does in the second and the equations can now be added:
\[ZnS+\dfrac{3}{2}O_2\rightarrow ZnO+SO_2\]
\[ZnO+CO\rightarrow Zn+CO_2\]
\[Adding \ these \ 2 \ yields:\]
\[ZnS+\dfrac{3}{2}O_2+ZnO+CO\rightarrow ZnO+SO_2 +Zn+CO_2\]
\[ZnS+\dfrac{3}{2}O_2 +CO\rightarrow SO_2 +Zn+CO_2\]
where \(ZnO\) has been ``canceled'' algebraically on both sides. From the overall reaction, we see that
or
Thus, the mass of \(Zn\) produced is
This is the theoretical yield predicted by the reaction equations. The actual yield is only \(3.30 \ kg), so that the fractional yield is
In multi-step processes, it is important that each step have as high a percentage yield as possible. The reason for this is that the overall percentage yield will be a product of the percentage yields of each step. As an example, suppose there is a 10-step process with a \(50\%\) yield for each step:
\[Step \ 1 \ - \ percentage \ yield=50\%\]
\[Step \ 2 \ - \ percentage \ yield=50\%\]
\[\vdots\]
\[Step \ 10 \ - \ percentage \ yield=50\%\]
The overall percentage yield would be the product of the individual percentages, or
Even if the percentage yield of each step were \(90\%\), the overall yield would be \((0.9)^{10}=35\%\), which is better, but still somewhat low. If the percentage yield of each step were \(95\%\), then the overall yield would be \((0.95)^{10}=60\%\), which might make the process feasible.


