12.5: Spectroscopy and the Electromagnetic Spectrum
- Page ID
- 67281
Objectives
After completing this section, you should be able to
- write a brief paragraph discussing the nature of electromagnetic radiation.
- write the equations that relate energy to frequency, frequency to wavelength and energy to wavelength, and perform calculations using these relationships.
- describe, in general terms, how absorption spectra are obtained.
Make certain that you can define, and use in context, the key terms below.
- electromagnetic radiation
- electromagnetic spectrum
- hertz (Hz)
- infrared spectroscopy
- photon
- quantum
From your studies in general chemistry or physics, you should be familiar with the idea that electromagnetic radiation is a form of energy that possesses wave character and travels through space at a speed of 3.00 × 108m · s−1. However, such radiation also displays some of the properties of particles, and on occasion it is more convenient to think of electromagnetic radiation as consisting of a stream of particles called photons.
In spectroscopy, the frequency of the electromagnetic radiation being used is usually expressed in hertz (Hz), that is, cycles per second. Note that 1 Hz = s−1.
A quantum is a small, definite quantity of electromagnetic radiation whose energy is directly proportional to its frequency. (The plural is “quanta.”) If you wish, you can read about the properties of electromagnetic radiation and the relationships among wavelength, frequency and energy, or refer to your general chemistry textbook if you still have it.
Note also that in SI units, Planck’s constant is 6.626 × 10−34 J · s.
The electromagnetic spectrum
Electromagnetic radiation, as you may recall from a previous chemistry or physics class, is composed of electrical and magnetic waves which oscillate on perpendicular planes. Visible light is electromagnetic radiation. So are the gamma rays that are emitted by spent nuclear fuel, the x-rays that a doctor uses to visualize your bones, the ultraviolet light that causes a painful sunburn when you forget to apply sun block, the infrared light that the army uses in night-vision goggles, the microwaves that you use to heat up your frozen burritos, and the radio-frequency waves that bring music to anybody who is old-fashioned enough to still listen to FM or AM radio.
Just like ocean waves, electromagnetic waves travel in a defined direction. While the speed of ocean waves can vary, however, the speed of electromagnetic waves – commonly referred to as the speed of light – is essentially a constant, approximately 300 million meters per second. This is true whether we are talking about gamma radiation or visible light. Obviously, there is a big difference between these two types of waves – we are surrounded by the latter for more than half of our time on earth, whereas we hopefully never become exposed to the former to any significant degree. The different properties of the various types of electromagnetic radiation are due to differences in their wavelengths, and the corresponding differences in their energies: shorter wavelengths correspond to higher energy.
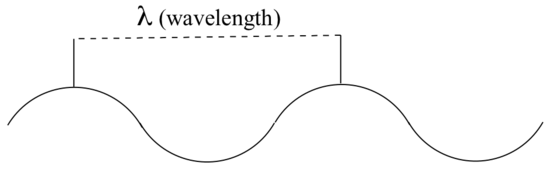
High-energy radiation (such as gamma- and x-rays) is composed of very short waves – as short as 10-16 meter from crest to crest. Longer waves are far less energetic, and thus are less dangerous to living things. Visible light waves are in the range of 400 – 700 nm (nanometers, or 10-9 m), while radio waves can be several hundred meters in length.
The notion that electromagnetic radiation contains a quantifiable amount of energy can perhaps be better understood if we talk about light as a stream of particles, called photons, rather than as a wave. (Recall the concept known as ‘wave-particle duality’: at the quantum level, wave behavior and particle behavior become indistinguishable, and very small particles have an observable ‘wavelength’). If we describe light as a stream of photons, the energy of a particular wavelength can be expressed as:
\[E = \dfrac{hc}{\lambda} \tag{12.5.1}\]
where E is energy in J, λ (the Greek letter lambda) is wavelength in meters, c is 3.00 x 108 m/s (the speed of light), and h is 6.626 × 10−34 J · s, a number known as Planck’s constant.
Because electromagnetic radiation travels at a constant speed, each wavelength corresponds to a given frequency, which is the number of times per second that a crest passes a given point. Longer waves have lower frequencies, and shorter waves have higher frequencies. Frequency is commonly reported in hertz (Hz), meaning ‘cycles per second’, or ‘waves per second’. The standard unit for frequency is s-1.
When talking about electromagnetic waves, we can refer either to wavelength or to frequency - the two values are interconverted using the simple expression:
\[ \lambda \nu = c \tag{12.5.2}\]
where ν (the Greek letter ‘nu’) is frequency in s-1. Visible red light with a wavelength of 700 nm, for example, has a frequency of 4.29 x 1014 Hz, and an energy of 2.84 x 10-19 J per photon or 171 kJ per mole of photons (remember Avogadro’s number = 6.02 × 1023 mol−1). The full range of electromagnetic radiation wavelengths is referred to as the electromagnetic spectrum.
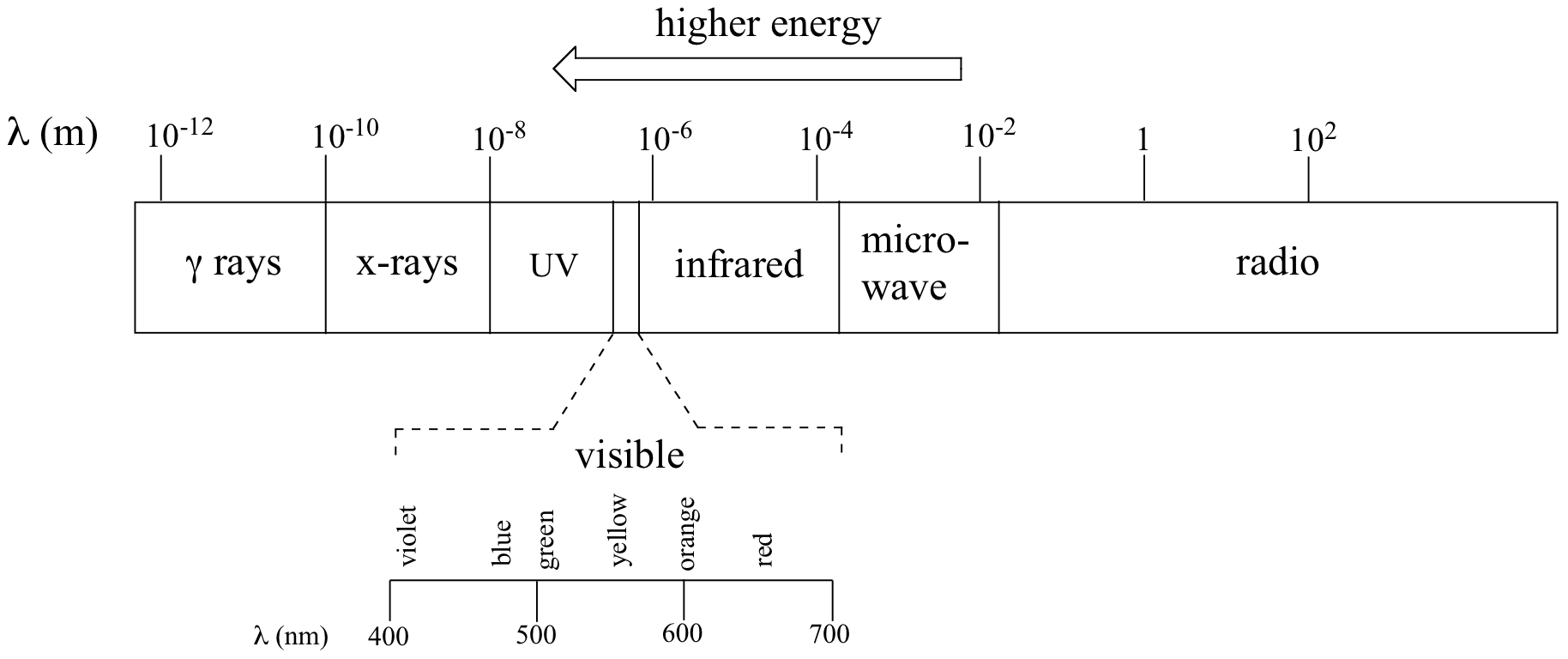
Notice in the figure above that visible light takes up just a narrow band of the full spectrum. White light from the sun or a light bulb is a mixture of all of the visible wavelengths. You see the visible region of the electromagnetic spectrum divided into its different wavelengths every time you see a rainbow: violet light has the shortest wavelength, and red light has the longest.
Visible light has a wavelength range of about 400-700 nm. What is the corresponding frequency range? What is the corresponding energy range, in kJ mol−1 of photons?
- Answer
-
Add texts here. Do not delete this text firstFor light with a wavelength of 400 nm, the frequency is 7.50 × 1014 Hz:
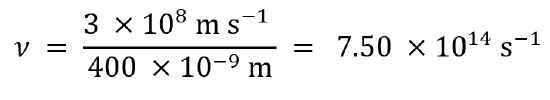
In the same way, we calculate that light with a wavelength of 700 nm has a frequency of 4.29 × 1014 Hz.
To calculate corresponding energies using hc/λ. We find for light at 400 nm:

Using the same equation, we find that light at 700 nm corresponds to 171 kJ mol−1.
Molecular spectroscopy – the basic idea
In a spectroscopy experiment, electromagnetic radiation of a specified range of wavelengths is allowed to pass through a sample containing a compound of interest. The sample molecules absorb energy from some of the wavelengths, and as a result jump from a low energy ‘ground state’ to some higher energy ‘excited state’. Other wavelengths are not absorbed by the sample molecule, so they pass on through. A detector on the other side of the sample records which wavelengths were absorbed, and to what extent they were absorbed.
Here is the key to molecular spectroscopy: a given molecule will specifically absorb only those wavelengths which have energies that correspond to the energy difference of the transition that is occurring. Thus, if the transition involves the molecule jumping from ground state A to excited state B, with an energy difference of ΔE, the molecule will specifically absorb radiation with wavelength that corresponds to ΔE, while allowing other wavelengths to pass through unabsorbed.
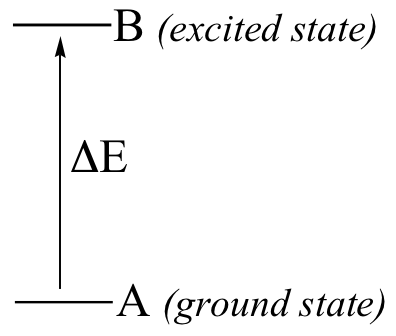
By observing which wavelengths a molecule absorbs, and to what extent it absorbs them, we can gain information about the nature of the energetic transitions that a molecule is able to undergo, and thus information about its structure.
These generalized ideas may all sound quite confusing at this point, but things will become much clearer as we begin to discuss specific examples.
Exercises
Which of the following frequencies/wavelengths are higher energy
A. λ = 2.0 x 10-6 m or λ= 3.0 x 10-9 m
B. υ = 3.0 x 109 Hz or υ= 3.0 x 10-6 Hz
- Answer
-
A. λ = 3.0 x 10-9 m
B. υ = 3.0 x 109 Hz
Calculate the energies (J) for the following;
A – Gamma Ray λ = 4.0 x 10-11 m
B – X-Ray λ = 4.0 x 10-9 m
C – UV light υ = 5.0 x 1015 Hz
D – Infrared Radiation λ = 3.0 x 10-5 m
E – Microwave Radiation υ = 3.0 x 1011 Hz
- Answer
-
The following are in joules.
A – 4.96 x 10-15
B – 4.96 x 10-17
C – 3.31 x 10-18
D – 6.62 x 10-21
E – 1.99 x 10-22
Contributors and Attributions
Dr. Dietmar Kennepohl FCIC (Professor of Chemistry, Athabasca University)
Prof. Steven Farmer (Sonoma State University)
William Reusch, Professor Emeritus (Michigan State U.), Virtual Textbook of Organic Chemistry

