1.3: Atomic Structure- Electron Configurations
- Page ID
- 67041
Objective
After completing this section, you should be able to write the ground-state electron configuration for each of the elements up to and including atomic number 36.
Make certain that you can define, and use in context, the key terms below.
- ground-state electronic configuration
- Hund's rule
- Pauli exclusion principle
- aufbau principle
The electron configuration of an element is the arrangement of its electrons in its atomic orbitals. By knowing the electron configuration of an element, we can predict and explain a great deal of its chemistry.
The Aufbau Principle
We construct the periodic table by following the aufbau principle (from German, meaning “building up”). First we determine the number of electrons in the atom; then we add electrons one at a time to the lowest-energy orbital available without violating the Pauli principle. We use the orbital energy diagram of Figure 6.29, recognizing that each orbital can hold two electrons, one with spin up ↑, corresponding to ms = +½, which is arbitrarily written first, and one with spin down ↓, corresponding to ms = −½. A filled orbital is indicated by ↑↓, in which the electron spins are said to be paired. Here is a schematic orbital diagram for a hydrogen atom in its ground state:
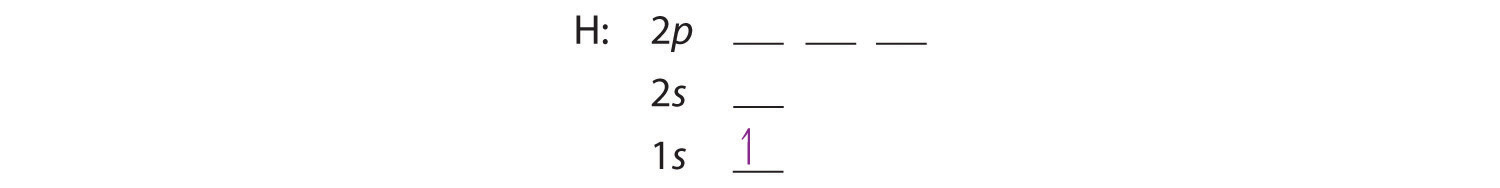
From the orbital diagram, we can write the electron configuration in an abbreviated form in which the occupied orbitals are identified by their principal quantum number n and their value of l (s, p, d, or f), with the number of electrons in the subshell indicated by a superscript. For hydrogen, therefore, the single electron is placed in the 1s orbital, which is the orbital lowest in energy (Figure 6.29"), and the electron configuration is written as 1s1 and read as “one-s-one.”
A neutral helium atom, with an atomic number of 2 (Z = 2), has two electrons. We place one electron in the orbital that is lowest in energy, the 1s orbital. From the Pauli exclusion principle, we know that an orbital can contain two electrons with opposite spin, so we place the second electron in the same orbital as the first but pointing down, so that the electrons are paired. The orbital diagram for the helium atom is therefore
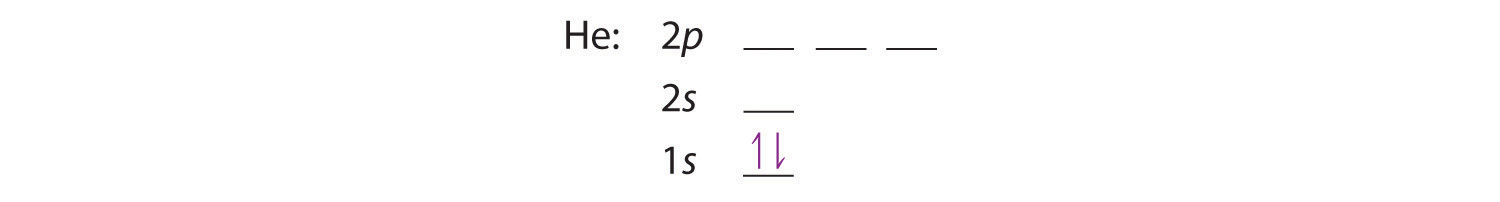
written as 1s2, where the superscript 2 implies the pairing of spins. Otherwise, our configuration would violate the Pauli principle.
The next element is lithium, with Z = 3 and three electrons in the neutral atom. We know that the 1s orbital can hold two of the electrons with their spins paired. Figure 6.29 tells us that the next lowest energy orbital is 2s, so the orbital diagram for lithium is
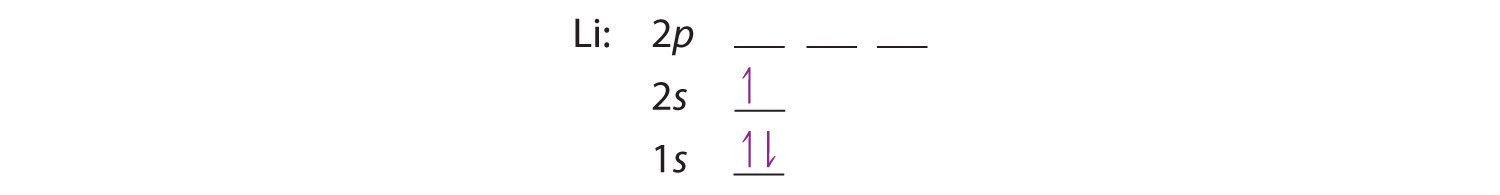
This electron configuration is written as 1s22s1.
The next element is beryllium, with Z = 4 and four electrons. We fill both the 1s and 2s orbitals to achieve a 1s22s2 electron configuration:
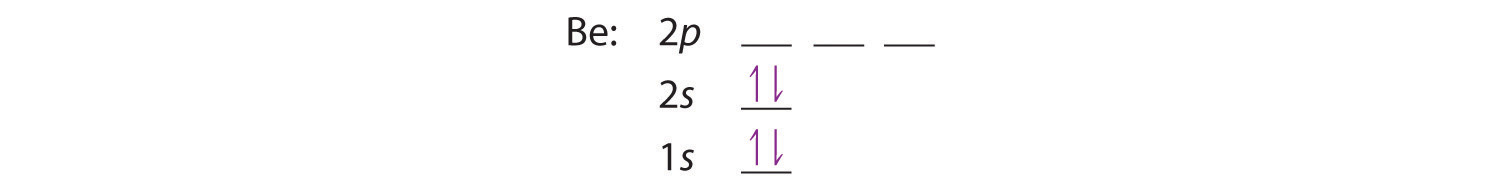
When we reach boron, with Z = 5 and five electrons, we must place the fifth electron in one of the 2p orbitals. Because all three 2p orbitals are degenerate, it doesn’t matter which one we select. The electron configuration of boron is 1s22s22p1:
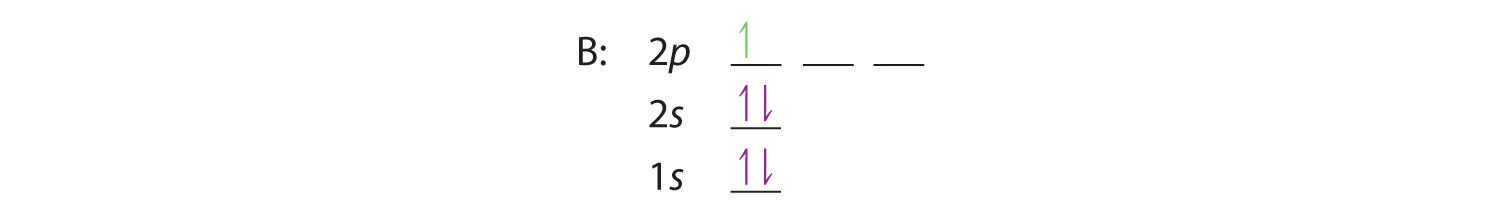
At carbon, with Z = 6 and six electrons, we are faced with a choice. Should the sixth electron be placed in the same 2p orbital that already has an electron, or should it go in one of the empty 2p orbitals? If it goes in an empty 2p orbital, will the sixth electron have its spin aligned with or be opposite to the spin of the fifth? In short, which of the following three orbital diagrams is correct for carbon, remembering that the 2p orbitals are degenerate?
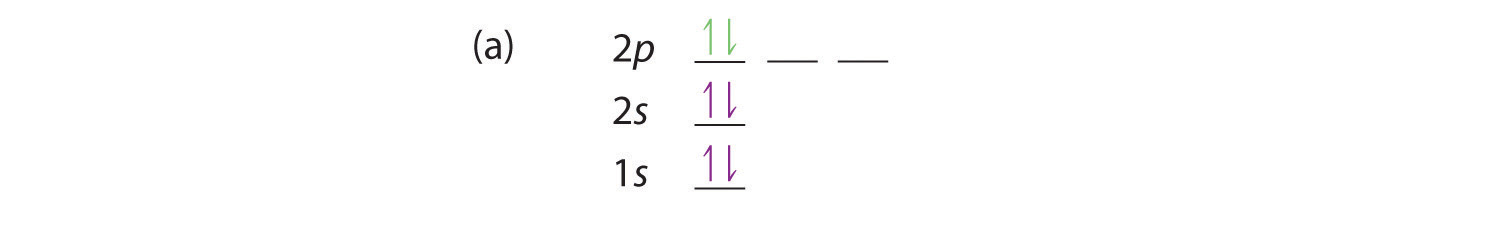
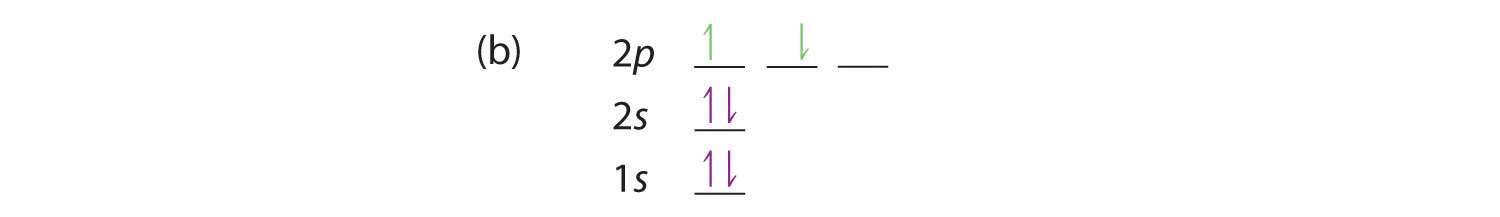
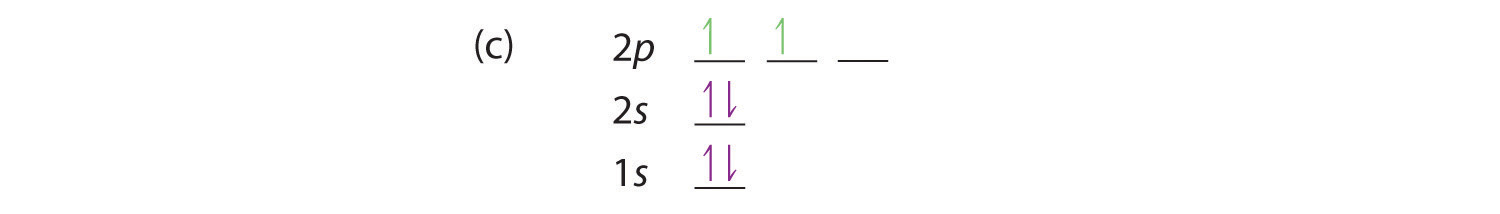
Because of electron-electron repulsions, it is more favorable energetically for an electron to be in an unoccupied orbital than in one that is already occupied; hence we can eliminate choice a. Similarly, experiments have shown that choice b is slightly higher in energy (less stable) than choice c because electrons in degenerate orbitals prefer to line up with their spins parallel; thus, we can eliminate choice b. Choice c illustrates Hund’s rule (named after the German physicist Friedrich H. Hund, 1896–1997), which today says that the lowest-energy electron configuration for an atom is the one that has the maximum number of electrons with parallel spins in degenerate orbitals. By Hund’s rule, the electron configuration of carbon, which is 1s22s22p2, is understood to correspond to the orbital diagram shown in c. Experimentally, it is found that the ground state of a neutral carbon atom does indeed contain two unpaired electrons.
When we get to nitrogen (Z = 7, with seven electrons), Hund’s rule tells us that the lowest-energy arrangement is
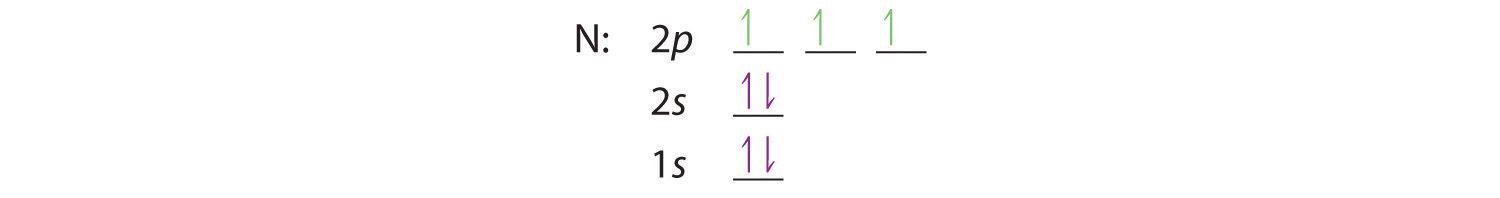
with three unpaired electrons. The electron configuration of nitrogen is thus 1s22s22p3.
At oxygen, with Z = 8 and eight electrons, we have no choice. One electron must be paired with another in one of the 2p orbitals, which gives us two unpaired electrons and a 1s22s22p4 electron configuration. Because all the 2p orbitals are degenerate, it doesn’t matter which one has the pair of electrons.
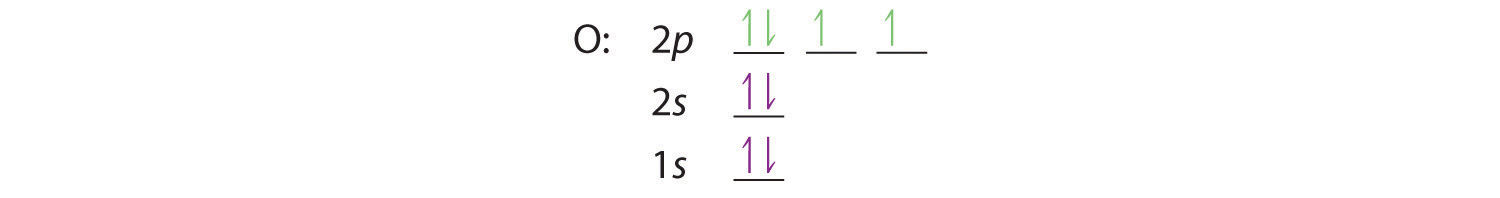
Similarly, fluorine has the electron configuration 1s22s22p5:
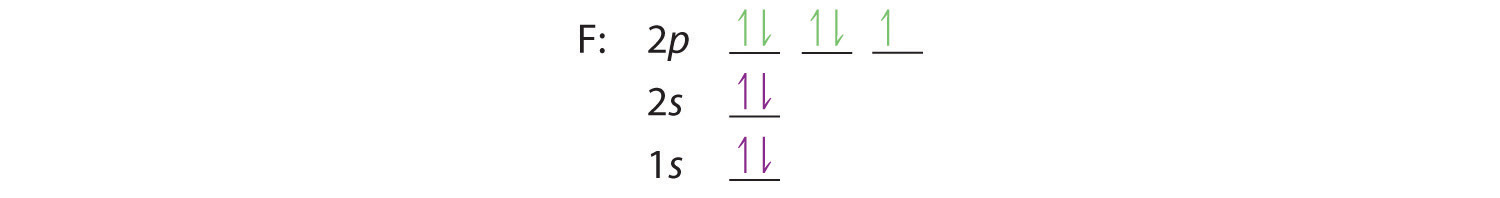
When we reach neon, with Z = 10, we have filled the 2p subshell, giving a 1s22s22p6 electron configuration:
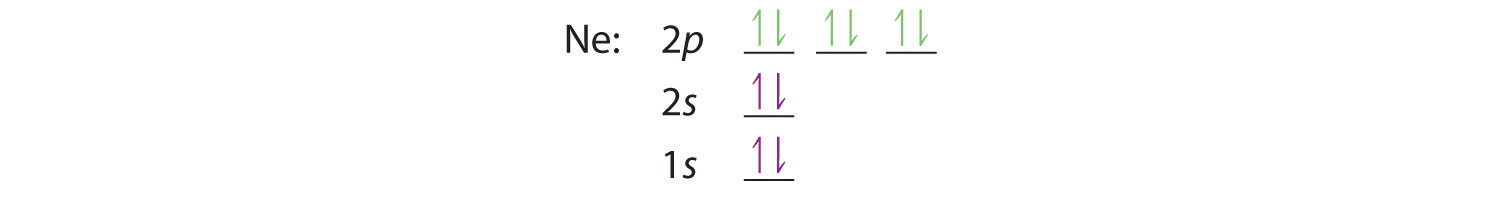
Notice that for neon, as for helium, all the orbitals through the 2p level are completely filled. This fact is very important in dictating both the chemical reactivity and the bonding of helium and neon, as you will see.
Valence Electrons
As we continue through the periodic table in this way, writing the electron configurations of larger and larger atoms, it becomes tedious to keep copying the configurations of the filled inner subshells. In practice, chemists simplify the notation by using a bracketed noble gas symbol to represent the configuration of the noble gas from the preceding row because all the orbitals in a noble gas are filled. For example, [Ne] represents the 1s22s22p6 electron configuration of neon (Z = 10), so the electron configuration of sodium, with Z = 11, which is 1s22s22p63s1, is written as [Ne]3s1:
| Neon | Z = 10 | 1s22s22p6 |
| Sodium | Z = 11 | 1s22s22p63s1 = [Ne]3s1 |
Because electrons in filled inner orbitals are closer to the nucleus and more tightly bound to it, they are rarely involved in chemical reactions. This means that the chemistry of an atom depends mostly on the electrons in its outermost shell, which are called the valence electrons. The simplified notation allows us to see the valence-electron configuration more easily. Using this notation to compare the electron configurations of sodium and lithium, we have:
| Sodium | 1s22s22p63s1 = [Ne]3s1 |
| Lithium | 1s22s1 = [He]2s1 |
It is readily apparent that both sodium and lithium have one s electron in their valence shell. We would therefore predict that sodium and lithium have very similar chemistry, which is indeed the case.
As we continue to build the eight elements of period 3, the 3s and 3p orbitals are filled, one electron at a time. This row concludes with the noble gas argon, which has the electron configuration [Ne]3s23p6, corresponding to a filled valence shell.
Draw an orbital diagram and use it to derive the electron configuration of phosphorus, Z = 15. What is its valence electron configuration?
Given: atomic number
Asked for: orbital diagram and valence electron configuration for phosphorus
Strategy:
- Locate the nearest noble gas preceding phosphorus in the periodic table. Then subtract its number of electrons from those in phosphorus to obtain the number of valence electrons in phosphorus.
- Referring to Figure 6.29, draw an orbital diagram to represent those valence orbitals. Following Hund’s rule, place the valence electrons in the available orbitals, beginning with the orbital that is lowest in energy. Write the electron configuration from your orbital diagram.
- Ignore the inner orbitals (those that correspond to the electron configuration of the nearest noble gas) and write the valence electron configuration for phosphorus.
Solution:
A Because phosphorus is in the third row of the periodic table, we know that it has a [Ne] closed shell with 10 electrons. We begin by subtracting 10 electrons from the 15 in phosphorus.
B The additional five electrons are placed in the next available orbitals, which Figure 6.29 tells us are the 3s and 3p orbitals:
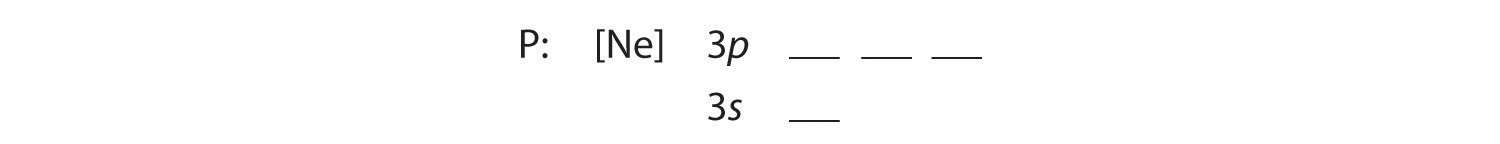
Because the 3s orbital is lower in energy than the 3p orbitals, we fill it first:
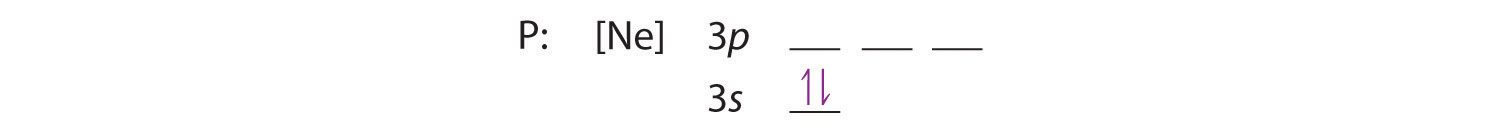
Hund’s rule tells us that the remaining three electrons will occupy the degenerate 3p orbitals separately but with their spins aligned:
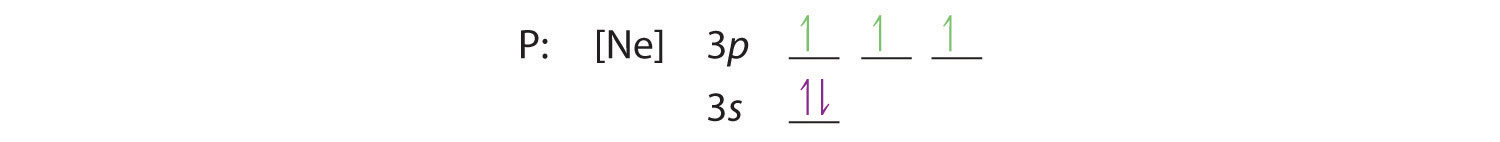
The electron configuration is [Ne]3s23p3.
C We obtain the valence electron configuration by ignoring the inner orbitals, which for phosphorus means that we ignore the [Ne] closed shell. This gives a valence-electron configuration of 3s23p3.
Draw an orbital diagram and use it to derive the electron configuration of chlorine, Z = 17. What is its valence electron configuration?
- Answer
- [Ne]3s23p5; 3s23p5
The general order in which orbitals are filled is depicted in Figure 1.3.1. Subshells corresponding to each value of n are written from left to right on successive horizontal lines, where each row represents a row in the periodic table. The order in which the orbitals are filled is indicated by the diagonal lines running from the upper right to the lower left. Accordingly, the 4s orbital is filled prior to the 3d orbital because of shielding and penetration effects. Consequently, the electron configuration of potassium, which begins the fourth period, is [Ar]4s1, and the configuration of calcium is [Ar]4s2. Five 3d orbitals are filled by the next 10 elements, the transition metals, followed by three 4p orbitals. Notice that the last member of this row is the noble gas krypton (Z = 36), [Ar]4s23d104p6 = [Kr], which has filled 4s, 3d, and 4p orbitals. The fifth row of the periodic table is essentially the same as the fourth, except that the 5s, 4d, and 5p orbitals are filled sequentially.
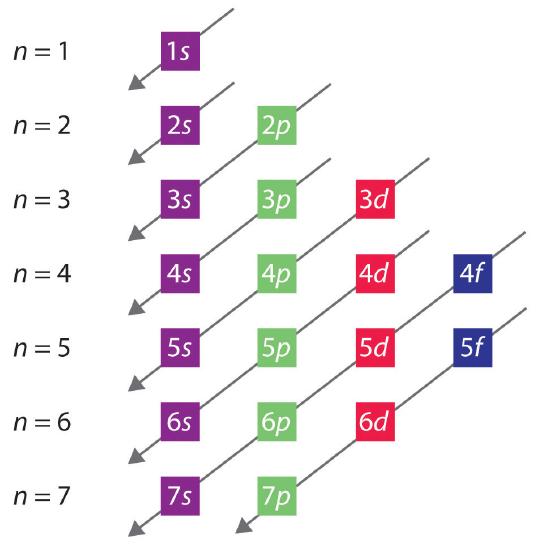
Figure 1.3.1: Predicting the Order in Which Orbitals Are Filled in Multielectron Atoms. If you write the subshells for each value of the principal quantum number on successive lines, the observed order in which they are filled is indicated by a series of diagonal lines running from the upper right to the lower left.
The sixth row of the periodic table will be different from the preceding two because the 4f orbitals, which can hold 14 electrons, are filled between the 6s and the 5d orbitals. The elements that contain 4f orbitals in their valence shell are the lanthanides. When the 6p orbitals are finally filled, we have reached the next (and last known) noble gas, radon (Z = 86), [Xe]6s24f145d106p6 = [Rn]. In the last row, the 5f orbitals are filled between the 7s and the 6d orbitals, which gives the 14 actinide elements. Because the large number of protons makes their nuclei unstable, all the actinides are radioactive.
Write the electron configuration of mercury (Z = 80), showing all the inner orbitals.
Given: atomic number
Asked for: complete electron configuration
Strategy:
Using the orbital diagram in Figure 1.3.1 and the periodic table as a guide, fill the orbitals until all 80 electrons have been placed.
Solution:
By placing the electrons in orbitals following the order shown in Figure 1.3.1 and using the periodic table as a guide, we obtain
| 1s2 | row 1 | 2 electrons |
| 2s22p6 | row 2 | 8 electrons |
| 3s23p6 | row 3 | 8 electrons |
| 4s23d104p6 | row 4 | 18 electrons |
| 5s24d105p6 | row 5 | 18 electrons |
| row 1–5 | 54 electrons |
1s22s22p63s23p64s23d104p65s24d105p66s24f145d10 = Hg = [Xe]6s24f145d10
with a filled 5d subshell, a 6s24f145d10 valence shell configuration, and a total of 80 electrons. (You should always check to be sure that the total number of electrons equals the atomic number.)
Give the electron configurations for Al, Br, and Fe.
- Answer
- Al = 1s22s22p63s23p1 Br = 1s22s22p63s23p64s23d104p5 Fe = 1s22s22p63s23p64s23d6
Summary
Based on the Pauli principle and a knowledge of orbital energies obtained using hydrogen-like orbitals, it is possible to construct the periodic table by filling up the available orbitals beginning with the lowest-energy orbitals (the aufbau principle), which gives rise to a particular arrangement of electrons for each element (its electron configuration). Hund’s rule says that the lowest-energy arrangement of electrons is the one that places them in degenerate orbitals with their spins parallel. For chemical purposes, the most important electrons are those in the outermost principal shell, the valence electrons.
Exercises
Contributors and Attributions
Dr. Dietmar Kennepohl FCIC (Professor of Chemistry, Athabasca University)
Prof. Steven Farmer (Sonoma State University)
William Reusch, Professor Emeritus (Michigan State U.), Virtual Textbook of Organic Chemistry
Organic Chemistry With a Biological Emphasis by Tim Soderberg (University of Minnesota, Morris)

