2.2: Formal Development
- Page ID
- 203342
A scientific theory is a conceptual framework for rationalizing sets of observations. The structure of a theory is to forward a set of fundamental postulates, which, if taken as truths lead to results that match observation. For example, Dalton's atomic theory posits such things as matter consisting of immutable atoms, where each atom is identified as belonging to an element, and the atoms of a given element are all identical. You can see that the discovery of isotopes required modification of that last point, for example, but the atomic theory as proposed by Dalton still describes much of chemistry. Theories are generally not entirely right or wrong, but they have varying levels of usefulness. Theories are rarely (if ever) complete.
The following is a set of formal postulates of the non-relativistic quantum theory. We have seen that the birth of quantum theory was intertwined with the birth of the theory of relativity, but the relativistic theory of quantum mechanics is still a work in progress (an area of considerable intellectual tumult, if general relativity is considered). However, there are systems for which the speed of light is effectively infinite compared to system velocities (\(p/m = v \ll c\)), and the non-relativistic theory suffices. (Similarly, very massive fast objects are handled well with relativity and no quantum mechanics). The majority of chemistry is described well without relativity (core electrons of ever heavier elements being an exception).
It is worth noting before we start that, while there is consensus on the minimal content of the postulates of quantum theory, their exact organization, including the number of postulates, varies from text to text. More abstract ways of looking at the theory can sometimes summarize what might be considered multiple postulates as one.
1. Postulate 1: Wavefunction for the state
The state of a physical system (e.g., a particle) is represented by a wavefunction, which, along with the particle identities, contains all physical information about the system.
This postulate has already been thoroughly discussed qualitatively in this text. We simply take a moment to draw an analogy between the wavefunction and the combined position and momentum of a classical particle. The position and momentum together define the physical state of a fundamental (internally structureless) classical particle of known identity. With only this information, and knowledge of the surrounding field in which it moves (perhaps time-dependent), the state of the particle at any later time may be predicted. There is nothing else to know about the particle itself. Similarly, there is no inquiry that one can make of a composite system of many particles that cannot be answered by knowing all the positions, momenta, and identities of all of the particles. In quantum mechanics, the state of a particle is fully described by a complex wave on its spatial coordinates. For a composite system, the state of the whole system is a wave on the space of the coordinates of all of the particles. There is nothing to know about the system that is not accessible through the total wave function at some given time, and knowledge of the particle identities. With additional knowledge of the surrounding external field, even its future state (or its history) can be determined.
There are a few formal details, however. Mainly, there are conditions on acceptable wavefunctions. Wavefunctions must be single-valued, continuous, and also have continuous first and second derivatives. They may not diverge, and they must be square integrable (the integral of the square modulus must be finite). All of the functions shown in the figure [#] below are inadmissible.

Two of the conditions, (c) and (e) in the figure [#] above, can be relaxed in practice, though not formally. Case (c) indicates a wavefunction with a "kink," which can be thought of as a place where the "local" wavelength goes suddenly to zero (opposite of having a very long wavelength, with nearly zero curvature). This would be interpreted as having infinite local kinetic energy at that point. In fact, this can happen if potentials are introduced having isolated points at which they diverge. However, no real physical systems have truly infinite potentials. The Coulomb potential diverges for volumeless point particles, but that is an idealization. Regarding case (e), wavefunctions that cannot be normalized will sometimes be introduced into a calculation, and this is a useful technique, but they do not represent the state of any actual system. Rather, they are idealizations that can then be summed together (generally integrated over) to produce proper wavefunctions. Such non-normalizable functions also represent mathematically limiting cases of very broad particle waves.
2. Postulate 2: Superposition principle
A linear combination (superposition) of any number of valid wavefunctions for a system is itself a valid wave function for that system.
A linear combination is a generalization of a sum, where (potentially complex) coefficients may multiply the functions that are summed or integrated together, with each function appearing only to the to the first power (i.e., linear, not squared, etc.). One of the most fundamental aspects of waves is that they exhibit interference patterns. The simplest example was already encountered in the double-slit experiment. The total wave may be constructed as the superposition (sum) of the waves that would result if only one or the other slit were open, as illustrated in the figure [#] below. The resulting interference pattern gives rise to the observable undulation in light intensity across the screen on the other side, which one would not see if only one slit were open; there would be no superposition or consequent interference.
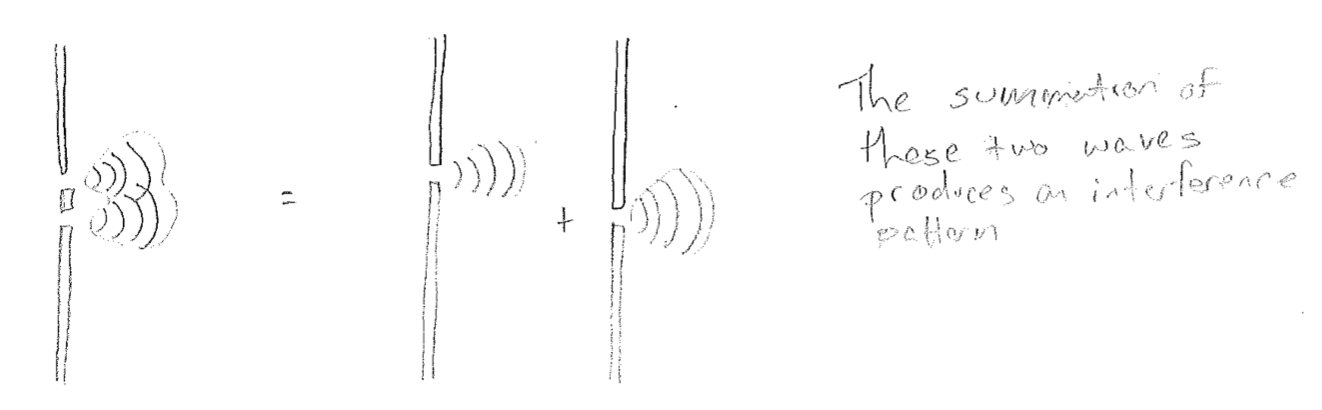
This superposition principle was hinted at already at the end of Postulate 1. It is essentially the second half of asserting that matter moves as waves. It may be considered an implicit consequence of Postulate 1, as opposed to a separate postulate. However, it is an important principle with its own oft-used name, and so we have discussed it separately.
3. Postulate 3: Operators for physical properties
Any physical property can be associated with a complete set of orthogonal wavefunctions, which each have a well-defined, real value for that property. This implies that these states are eigenfunctions of a self-adjoint (Hermitian) linear operator corresponding to that property, where the allowed property values are the eigenvalues associated with each eigenfunction.
a. complete sets of states
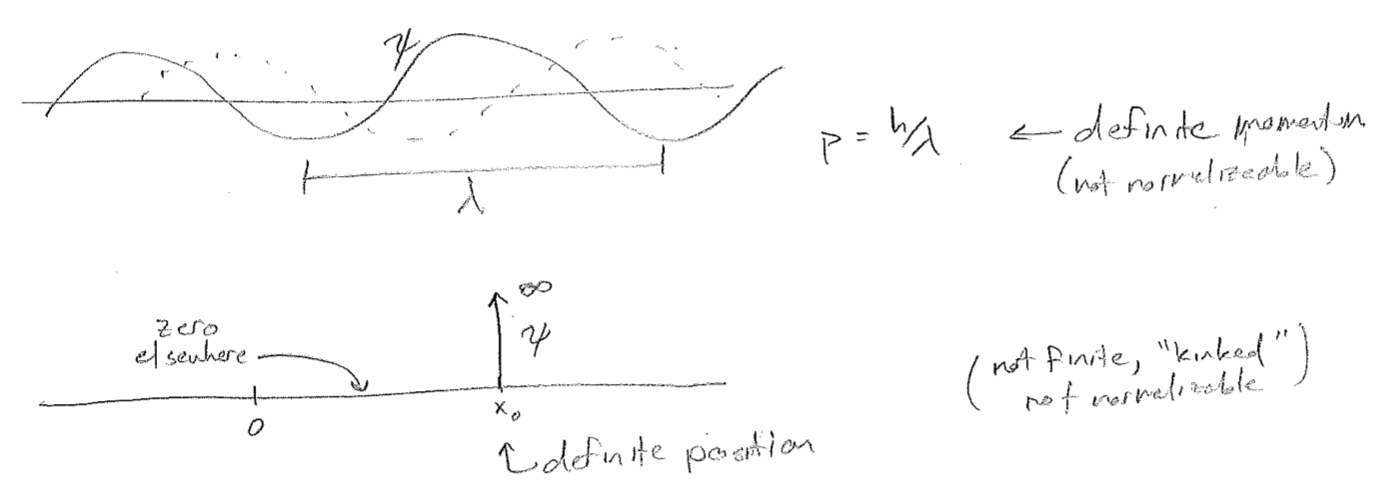
This postulate has a rather complex structure. Let us take each concept in turn. First, we will illustrate what is meant by a "complete" set by examining those wavefunctions that we know to have either well-defined momentum or position in 1D, which are illustrated in the figure [#] above. All such functions of either kind build a complete set of orthogonal functions. To be complete means that any admissible wavefunction (in 1D) may be constructed as a superposition of the members of that set (even if, by themselves, they do not meet all admissibility criteria).
For example, though we do not delve into the mathematical details, the restrictions we have put on an admissible wavefunction \(\psi(x)\) assure us that it may be expressed as
\[
\psi(x)=\int_{-\infty}^{\infty} \text{d} \bar{\nu}~\phi(\bar{\nu}) \, \text{e}^{\text{i} 2 \pi \bar{\nu} x}
\label{fourier}\]
for some equally well behaved choice of \(\phi(\bar{\nu})\). Mathematicians call \(\phi(\bar{\nu})\) the Fourier transform of \(\psi(x)\). We see that integration has the effect of “summing” all possible plane-wave functions (with different \(\bar{\nu}\)) giving different amplitude \(\phi(\bar{\nu})\) to each. The fact that any admissible \(\psi(x)\) in 1D may be written as such is what we mean by saying that the set of all plane waves \(\big\{\text{e}^{\text{i}2\pi\bar{\nu}x}\big\}\) is complete. Note that it is not problematic that the plane waves themselves are inadmissible wavefunctions; all this means is that the set is bigger than it needs to be, in order to be complete in the sense required here. The plane waves can also build infinitely many inadmissible wavefunctions, in addition to the admissible ones.
Now let us illustrate the completeness of the definite-position functions. The theory of such mathematical objects is quite advanced, but for the purposes of this text, the following definition will suffice for the Dirac delta function \(\delta(x)\), which is centered at the origin:
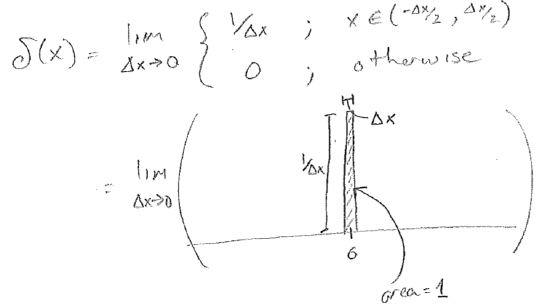
A \(\delta\)-function located elsewhere, at \(x_0\), may simply be written as \(\delta(x-x_0)\), a translation of the function in eqn. [not numbered, found in “figure [#]” above]. Let us then consider the mechanics of the following identity
\[\begin{align}
\psi(x)
&=\int_{-\infty}^{\infty} \text{d} x^{\prime} ~ \psi(x^{\prime}) \, \delta(x-x^{\prime}) \nonumber\\
&=\lim _{\varepsilon \rightarrow 0} \int_{x-\varepsilon}^{x+\varepsilon} \text{d} x^{\prime}\psi(x^{\prime}) \, \delta(x-x^{\prime}) \nonumber\\
&=\psi(x) \, \lim _{\varepsilon \rightarrow 0} \int_{x-\varepsilon}^{x+\varepsilon} \text{d} x^{\prime} \, \delta(x-x^{\prime}) \nonumber\\
&=\psi(x) \, \lim _{\varepsilon \rightarrow 0} \int_{+\varepsilon}^{-\varepsilon} -\text{d} u~\delta(u) \nonumber\\
&=\psi(x) \, \lim _{\varepsilon \rightarrow 0} \int_{-\varepsilon}^{+\varepsilon} \text{d} u~\delta(u) \nonumber\\&= \psi(x)
\end{align}\]
This identity rests on the fact that, since the \(\delta\)-function is infinitely narrow, the integration bounds can be brought to the point where only a single value of \(\psi(x^{\prime})\) matters, and then the unit area of the \(\delta\)-function “plucks out” only this value. (Technically, this identity defines the \(\delta\)-function, and that gives rise to the interpretation of the function as we have drawn it.) The mechanics of the identity aside, it reads analogously to the Fourier transform of eqn. \ref{fourier}; any function \(\psi(x)\) may be built by “summing" the \(\delta\)-functions at every point in space. It makes good sense that the amplitude for each position function is the wavefunction itself at that same point. Finally, in analogy to the plane waves, the set of \(\delta\)-functions is not only complete, but it could also be used to build inadmissible wavefunctions, so this set of functions is also bigger than complete (for the purpose of building admissible 1D wavefunctions).
In the concrete context of 1D states that we already understand to have either definite momentum (the plane waves) or definite position (the \(\delta\)-functions), we have illustrated that either such set is complete. So, the properties of both momentum and position are associated with complete sets of states, which correspond to its allowed values.
b. orthogonal states
The discussion of the first sentence of the third postulate has thus far only left the word “orthogonal” to be addressed. The physical interpretation of orthogonality is that the waves corresponding to different values of some physical property are completely distinct from one another. Geometrically, it means that one function contains no component of another function to which it is said to be orthogonal, in analogy to what is meant by orthogonal vectors. This is most intuitive for the set of position functions; clearly a \(\delta\)-function centered at one point will have no amplitude in building a \(\delta\)-function centered at a different point. Mathematically, if two functions in 1D, \(f(x)\) and \(g(x)\), are normalizable, they are said to also be orthogonal if
\[
\int_{-\infty}^{\infty} \text{d}x\; f^{*\!}(x) \, g(x)=0
\]
Where the asterisk (\({}^{*\!}\)) denotes the taking of a complex conjugate. One might clearly see the physical interpretation that, if \(f(x)\) and \(g(x)\) are very different from each other (e.g., very far from each other), then this integral will go to zero for these "distinct" functions, but it certainly would not if they were the same, or even quite similar. The word "orthogonal" is used because of the relationship of this integral to the formula for the dot product of vectors (when the integration is written as a Riemann sum); it is, in fact a rigorous generalization of orthogonality to "spaces" of functions. In the case where the functions are not normalizable (say, for plane waves or \(\delta\)-functions), the following holds for orthogonal functions in 1D
\[
0=
\lim _{L \rightarrow \infty} \frac{\int_{-L}^{L} \text{d}x\; f^{*\!}(x)\,g(x)}{\int_{-L} ^{L}\text{d}x~|f(x)|^{2}}=\lim _{L \rightarrow \infty} \frac{\int_{-L}^{L} \text{d}x\; f^{*\!}(x) \, g(x)}{\int_{-L}^{L} \text{d}x~|g(x)|^{2}}
\]
In this case, the denominator diverges, but the numerator does not.
c. operators
We are now in a position to handle the second sentence of this postulate concerning Hermitian operators. We will start by demonstrating that we that we can find "operators" whose "eigenfunction–eigenvalue" pairs are the 1D definite-position and definite-momentum wavefunctions just introduced. In the course of doing so, our purpose is to introduce the concepts of linear operators, eigenfunctions, and eigenvalues.
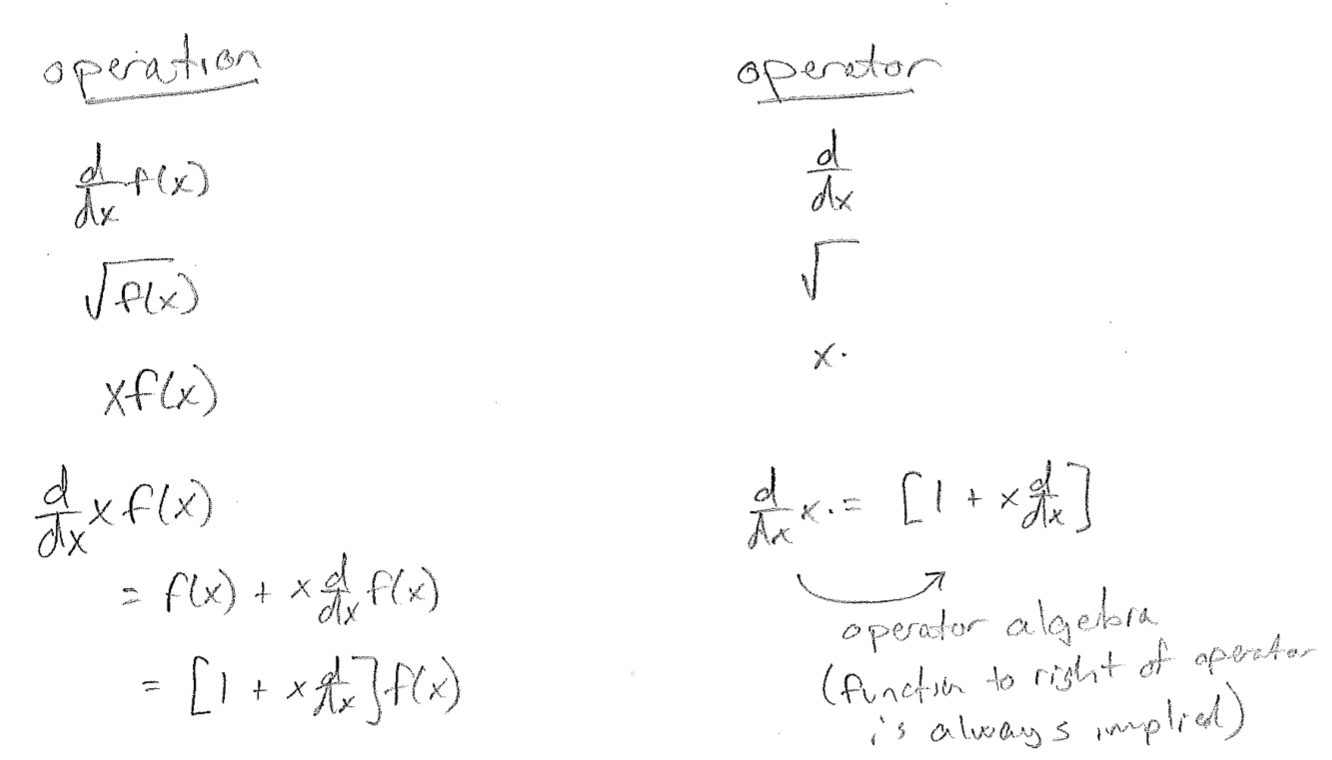
First, we discuss the concept of operators, specifically, linear operators. An operation on a mathematical function is anything that is done to a function which produces another function on that same set of coordinates (such as multiplication or differentiation). From any operation, we can abstract an operator. For example, those shown in the table [#] above. The last of these provides a good example of how operators themselves have their own set of manipulations and equalities, which can be gleaned by always assuming that there is some arbitrary function to the right of them. In this text, we will follow a typical convention of distinguishing an operator by a “hat,” when referenced symbolically. For example (for operators that will be discussed more shortly)
\[\begin{align}
\hat{x} = x\cdot \quad\quad\quad &(\text{position along the x axis, multiplication by} ~x) \\
\hat{p}_\text{x} = -\text{i} \hbar \frac{\partial}{\partial x} \quad\quad &(\text{momentum in the x direction})
\end{align}\]
Operators may be linear or nonlinear, depending on whether they obey a generalized distributive property (i.e., depending on how they act on linear combinations of functions). For example, in considering the examples,
\[\begin{align}
\frac{\text{d}}{\text{d}x}\big(f(x)+g(x)\big) &= \frac{\text{d}}{\text{d}x} f(x)+\frac{\text{d}}{\text{d}x} g(x) \\
\sqrt{f(x)+g(x)} &\neq \sqrt{f(x)}+\sqrt{g(x)}
\text{,}\end{align}\]
we say that the differential in the first example is a linear operator because it can be distributed over a linear combination of the functions \(f(x)\) and \(g(x)\), whereas this is not a valid manipulation for the square-root operator in the second example, meaning that it does not obey the definition of a linear operator. All operators corresponding to properties in quantum mechanics are linear operators. An important note is in order: although the operators we will meet will all have this “distributive” property, they will not usually have a commutative property. For example,
\[
\hat{x}\,\hat{p}_\text{x} ~\neq~ \hat{p}_\text{x}\,\hat {x}.
\]
We say that \(\hat{x}\) and \(\hat{p}_\text{x}\) do not commute.
d. eigenfunctions and eigenvalues
With this basic concept of operators in hand, let us now discuss one of their important properties, which is that an operator may have eigenfunctions, each with an associated eigenvalue. An eigenvalue–eigenfunction pair for some operator \(\hat{a}\) on 1D functions is a constant \(a_i\) and a function \(f_{i}(x)\) that satisfy
\[
\hat{a}\, f_{i}(x)=a_{i}\, f_{i}(x)
\]
Clearly, only functions with a special relationship to \(\hat{a}\) have this property. There are generally infinitely many such functions (a complete set, in fact) for a given \(\hat{a}\), hence the index \(i\).
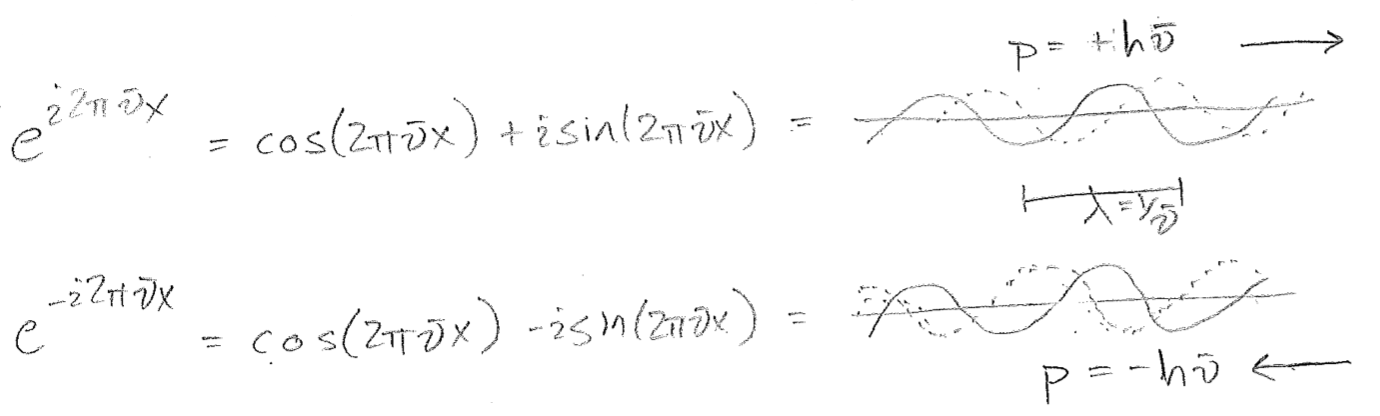
Let us now show that the 1D plane waves illustrated in the figure [#] above, which we associate with well-defined momenta, are indeed eigenfunctions of the operator that we have just asserted to be momentum operator, \(\hat{p}_\text{x}\), and have eigenvalues equal to the momentum associated with that wave. Recall that the relationship should be \(p=h / \lambda = h\bar{\nu}\), and that complex waves are necessary to define the direction of travel, which is critical for momentum. Inserting these presumed eigenfunctions into the eigenvalue equation for \(\hat{p}_\text{x}\) we verify this property as
\[\begin{align}
\hat{p}_\text{x} \, \text{e}^{\pm \text{i} 2 \pi \bar{\nu} x}
&=-\text{i} \hbar \frac{\partial}{\partial x} \text{e}^{\pm \text{i} 2 \pi \bar{\nu} x} \nonumber\\
&=(-\text{i} \hbar)(\pm \text{i} 2 \pi \bar{\nu}) \, \text{e}^{\pm \text{i} 2 \pi \bar{\nu} x} \nonumber\\
&=\pm h\bar{\nu}\, \text{e}^{\pm \text{i} 2 \pi \bar{\nu} x} \nonumber\\
&=p_\text{x}\, \text{e}^{\pm \text{i} 2 \pi \bar{\nu} x}
\end{align}\]
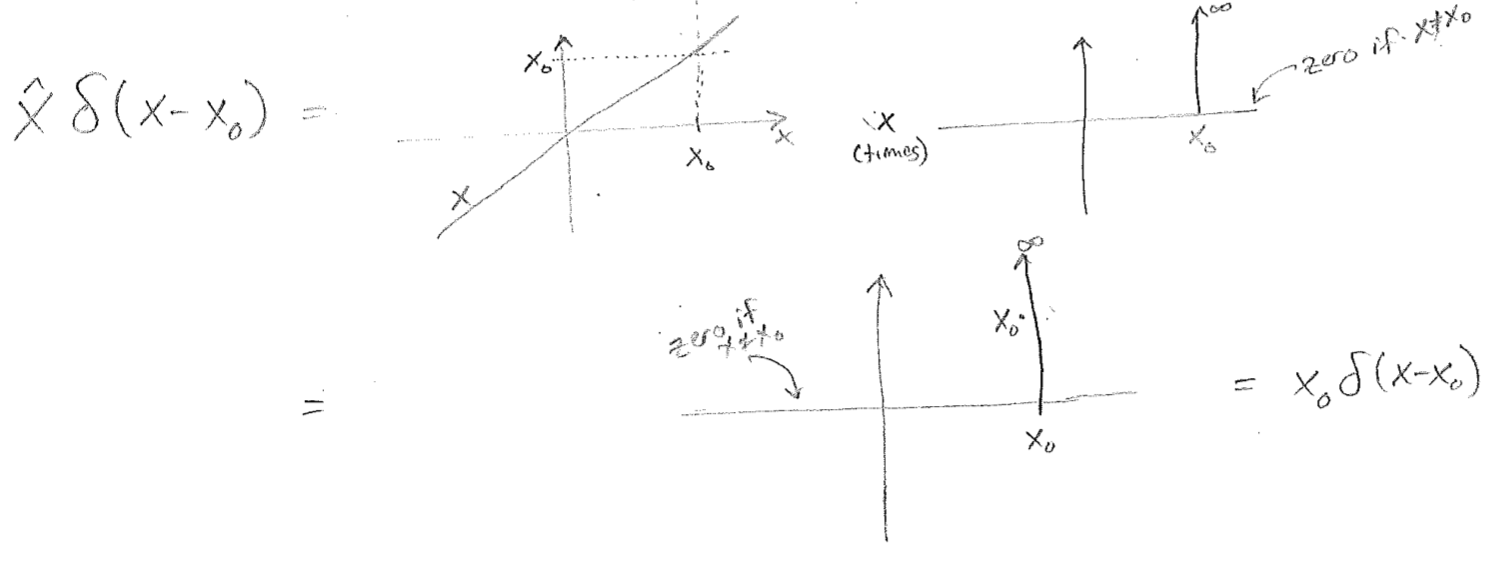
We can also show that the functions with definite position in 1D, the \(\delta\)-functions, are eigenfunctions of the position operator \(\hat{x}=x\cdot\), with eigenvalue corresponding to the position. Since the full theory of these advanced mathematical objects is beyond the scope of this text, we will illustrate this only graphically, as shown in the figure [#] below. We have now seen that, indeed, for position and momentum, there do exist operators, \(\hat{x}\) and \(\hat{p}_\text{x}\), whose eigenfunctions are states with eigenvalues that are the associated property for that state.
The final qualifier to address is that the operators are Hermitian. An operator \(\hat{a}\) in 1D is said to be Hermitian if, for two normalizable functions \(f(x)\) and \(g(x)\), it is true that
\[
\int_{-\infty}^{\infty} \text{d}x\;f^{*\!}(x) \, \hat{a} \, g(x) = \bigg[\int_{-\infty}^{\infty} \text{d}x\;g^{*\!}(x) \, \hat{a} \, f(x)\bigg]^*
\text{.}\]
This can be illustrated by writing \(f(x)\) and \(g(x)\) as linear combinations the eigenfunctions of \(\hat{a}\), which are presumed to build a complete set (possibly an overcomplete set) of orthogonal functions, having real eigenvalues (corresponding to the values of physical properties). This demonstration is left as an exercise for the reader.
In many texts, the discussion of the third postulate is reversed from how it is done here. A reader were versed well in linear algebra might recognize that the second second sentence in the third postulate is a consequence of the first one. The existence of a complete set of orthogonal functions, each with an associated real value, is all that is needed to construct a Hermitian linear operator. We could, therefore, have started with the statement that every property corresponds to a Hermitian linear operator on the space of valid wavefunctions, and then proceed to invoke the known mathematical properties of Hermitian operators (i.e., that they have as their eigenfunctions a complete set of orthogonal functions, whose eigenvalues are real) to complete the discussion of having states with well-defined values for the property under discussion. However, given the flow of the text up until the introduction of this postulate, we have preferred to begin with states and then move on to operators.
Our discussion of the physical content of the third postulate would, in fact, have been complete, without ever mentioning the connection to operators. However, discussion of the fourth postulate would be very cumbersome without it. Indeed, this is the utility of reaching for higher levels of mathematical abstraction within physics, and, should we have foregone this discussion, we would have also found ourselves uncomfortably distant from the operator language ubiquitously used, so much so that we have even given this third postulate the short title of “Operators for physical properties.”
4. Postulate 4: Measurement probabilities
content
5. Postulate 5: Time evolution
content


