8.6: The pH Concept
- Page ID
- 58829
Learning Outcomes
- Calculate between pH/\(\left[ \ce{H^+} \right]\) and pOH/\(\left[ \ce{OH^-} \right]\)
- Convert among pH, pOH, hydrogen-ion concentration, and hydroxide-ion concentration for a given solution.
Self-Ionization of Water
Water is a molecular compound, so you may not necessarily expect it to break apart into ions. However, sensitive experiments show that water is actually a very weak electrolyte. When two molecules of water collide, there can be a transfer of a hydrogen ion from one molecule to the other. The products are a positively charged hydronium ion and a negatively charged hydroxide ion.
\[\ce{H_2O} \left( l \right) + \ce{H_2O} \left( l \right) \rightleftharpoons \ce{H_3O^+} \left( aq \right) + \ce{OH^-} \left( aq \right)\]
The self-ionization of water is the process in which water ionizes to hydronium ions and hydroxide ions. As with other aqueous acid-base reactions, the process is often simplified to show the ionization of just one water molecule into a hydrogen ion and a hydroxide ion.
\[\ce{H_2O} \left( l \right) \rightleftharpoons \ce{H^+} \left( aq \right) + \ce{OH^-} \left( aq \right)\]
Either equation is adequate, though the first is more accurate, since hydrogen ions in aqueous solution will always be attached to water molecules. Further discussion of acids and acid ionizations in this book will primarily show hydrogen ions in aqueous solution as \(\ce{H^+}\), but keep in mind that this is just a commonly used abbreviation for the more accurate hydronium \(\left( \ce{H_3O^+} \right)\) structure.
In pure water, the concentrations of hydrogen and hydroxide ions are equal to one another. Any aqueous solution in which \(\left[ \ce{H^+} \right] = \left[ \ce{OH^-} \right]\) is said to be neutral.
For any neutral solution at \(25^\text{o} \text{C}\), each of these ions has a concentration of \(1.0 \times 10^{-7} \: \text{M}\).
An acidic solution is a solution in which the concentration of hydrogen ions is greater than the concentration of hydroxide ions. For example, hydrogen chloride ionizes to produce \(\ce{H^+}\) and \(\ce{Cl^-}\) ions upon dissolving in water.
\[\ce{HCl} \left( g \right) \rightarrow \ce{H^+} \left( aq \right) + \ce{Cl^-} \left( aq \right)\]
This increases the concentration of \(\ce{H^+}\) ions in the solution.
A basic solution is a solution in which the concentration of hydroxide ions is greater than the concentration of hydrogen ions. Solid potassium hydroxide dissociates in water to yield potassium ions and hydroxide ions.
\[\ce{KOH} \left( s \right) \rightarrow \ce{K^+} \left( aq \right) + \ce{OH^-} \left( aq \right)\]
The pH Scale
Expressing the acidity of a solution by using the molarity of the hydrogen ion is cumbersome because the quantities are generally very small. Danish scientist Søren Sørensen (1868 - 1939) proposed an easier system for indicating the concentration of \(\ce{H^+}\) called the pH scale. The letters pH stand for the power of the hydrogen ion. The pH of a solution is the negative logarithm of the hydrogen-ion concentration.
\[\text{pH} = -\text{log} \: \left[ \ce{H^+} \right]\]
In pure water or a neutral solution \(\left[ \ce{H^+} \right] = 1.0 \times 10^{-7} \: \text{M}\). Substituting this value into the pH expression:
\[\text{pH} = -\text{log} \: \left[ 1.0 \times 10^{-7} \right] = -\left( -7.00 \right) = 7.00\]
The pH of pure water or any neutral solution is thus 7.00. Due to the somewhat less intuitive rules for dealing with significant figures in the context of logarithms, only the numbers ot the right of the decimal point in the pH value are the significant figures. Since \(1.0 \times 10^{-7}\) has two significant figures, the pH can be reported as 7.00.
A logarithmic scale condenses the range of acidity to numbers that are easy to use. For example, a solution in which \(\left[ \ce{H^+} \right] = 1.0 \times 10^{-4} \: \text{M}\) has a hydrogen-ion concentration that is 1000 times higher than in pure water. The pH of such a solution is 4.00, a difference of 3 pH units. Notice that when \(\left[ \ce{H^+} \right]\) is written in scientific notation and the coefficient is 1, the pH is simply the exponent with the sign changed. The pH of a solution in which \(\left[ \ce{H^+} \right] = 1.0 \times 10^{-2} \: \text{M}\) is 2.0 and the pH of a solution in which \(\left[ \ce{H^+} \right] = 1.0 \times 10^{-10} \: \text{M}\) is 10.0. If the coefficient is not equal to 1, a calculator must be used to find the pH. For example, the pH of a solution in which \(\left[ \ce{H^+} \right] = 2.3 \times 10^{-5} \: \text{M}\) can be found as shown below.
\[\text{pH} = -\text{log} \: \left[ 2.3 \times 10^{-5} \right] = 4.64\]
As we saw earlier, a solution in which \(\left[ \ce{H^+} \right]\) is higher than \(1 \times 10^{-7} \: \text{M}\) acidic, while a solution in which \(\left[ \ce{H^+} \right]\) is lower than \(1.0 \times 10^{-7} \: \text{M}\) is basic. Consequently, solutions with pH values of less than 7 are acidic, while solutions with pH values higher than 7 are basic. The figure below illustrates this relationship, along with some examples of the pH for various solutions.

The pH scale is generally presented as running from 0 to 14, though it is possible to have a pH of less than 0 or greater than 14. For example, a highly concentrated \(3.0 \: \text{M}\) of \(\ce{HCl}\) has a negative pH.
\[\text{pH} = -\text{log} \left( 3.0 \right) = -0.48\]
When the pH of a solution is known, the concentration of the hydrogen ion can be calculated. The inverse of the logarithm (or antilog) is the \(10^x\) key on a calculator.
\[\left[ \ce{H^+} \right] = 10^{-\text{pH}}\]
For example, suppose that you have a solution with a pH of 9.14. \(\left[ \ce{H^+} \right]\) c an be found as follows:
\[\left[ \ce{H^+} \right] = 10^{-\text{pH}} = 10^{-9.14} = 7.24 \times 10^{-10} \: \text{M}\]
The pOH Concept
As with the hydrogen-ion concentration, the concentration of the hydroxide ion can be expressed logarithmically by the pOH. The pOH of a solution is the negative logarithm of the hydroxide-ion concentration.
\[\text{pOH} = -\text{log} \: \left[ \ce{OH^-} \right]\]
The pH of a solution can be related to the pOH. Consider a solution with pH \(=\) 4.0. The pOH of the solution would be 10. This example illustrates the following relationship. This is a result of the concentration of the \(\ce{H^+}\) and \(\ce{OH^-}\) ions present in pure water which we will not discuss further.
\[\text{pH} + \text{pOH} = 14\]
The pOH scale is similar to the pH scale, in that a pOH of 7 is indicative of a neutral solution. A basic solution has a pOH of less than 7, while an acidic solution has a pOH of greater than 7. The pOH is convenient to use when finding the hydroxide ion concentration from a solution with a known pH.
Example \(\PageIndex{1}\)
Find the hydroxide concentration of a solution with a pH of 4.42.
Solution
Step 1: List the known values and plan the problem.
Known
- pH \(=\) 4.42
- pH \(+\) pOH \(=\)14
Unknown
- \(\left[ \ce{OH^-} \right]\)
First, the pOH is calculated, followed by the \(\left[ \ce{OH^-} \right]\)
Step 2: Solve.
\[\text{pOH} = 14 - \text{pH} = 14 - 4.42 = 9.58\]
\[\left[ \ce{OH^-} \right] = 10^{-\text{pOH}} = 10^{-9.58} = 2.6 \times 10^{-10} \: \text{M}\]
Step 3: Think about your result.
The pH is that of an acidic solution, and the resulting hydroxide-ion concentration is less than \(1 \times 10^{-7} \: \text{M}\). The answer has two significant figures because the given pH has two decimal places.
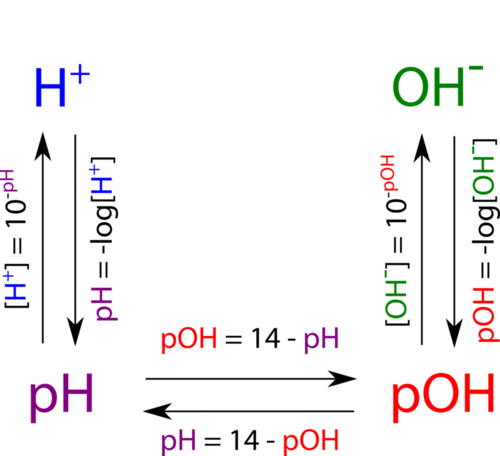
The diagram below shows all of the interrelationships between \(\left[ \ce{H^+} \right]\), \(\left[ \ce{OH^-} \right]\), pH, and pOH.
Contributors and Attributions
Allison Soult, Ph.D. (Department of Chemistry, University of Kentucky)

