4.3: Electron Group Geometry
- Page ID
- 58806
Learning Outcomes
- Explain the basis of VSEPR theory.
- Predict the shapes of molecules using VSEPR theory.
- Predict bond angles in a molecule.
- Account for variations in bond angles on the relative repulsive forces exerted by lone pairs and bonding pairs of electrons.
Electron group geometry is the three-dimensional arrangement of atoms in a molecule. The geometry of a molecule is an important factor that affects the physical and chemical properties of a compound. Those properties include melting and boiling points, solubility, density, and the types of chemical reactions that a compound undergoes. In this section, you will learn a technique to predict the geometry of a molecule based on a its Lewis electron dot structure.
VSEPR Theory
The valence shell is the outermost occupied shell of electrons in an atom. This shell holds the valence electrons, which are the electrons that are involved in bonding and shown in a Lewis structure. Valence-shell electron pair repulsion theory, or VSEPR theory, states that a molecule will adjust its shape so that the valence electron pairs stay as far apart from each other as possible. This makes sense, based on the fact that negatively charged electrons repel one another. We will systematically classify molecules according to the number of bonding pairs of electrons and the number of nonbonding or lone pairs around the central atom. For the purposes of the VSEPR model, a double or triple bond is no different in terms of repulsion than a single bond. We will begin by examining molecules in which the central atom does not have any lone pairs.
Central Atom with No Lone Pairs
In order to easily understand the types of molecules possible, we will use a simple system to identify the parts of any molecule.
\(\ce{A} =\) central atom in a molecule
\(\ce{B} =\) atoms surrounding the central atom
Subscripts after the \(\ce{B}\) will denote the number of \(\ce{B}\) atoms that are bonded to the central \(\ce{A}\) atom. For example, \(\ce{AB_4}\) is a molecule with a central atom surrounded by four covalently bonded atoms. Again, it does not matter if those bonds are single, double, or triple bonds.
\(\ce{AB_2}\)
Beryllium hydride \(\left( \ce{BeH_2} \right)\) consists of a central beryllium atom with two single bonds to hydrogen atoms. Note that it violates the octet rule, because the central atom has only 4 valence electrons. This is acceptable because beryllium only has two valence electrons to begin with, so it is not possible for it to create more than two covalent bonds with hydrogen atoms.
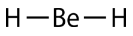
According to the requirement that electron pairs maximize their distance from one another, the two bonding pairs in the \(\ce{BeH_2}\) molecules will arrange themselves on directly opposite sides of the central \(\ce{Be}\) atom. The resulting geometry is a linear molecule, shown in a "ball-and-stick" model in the figure below.
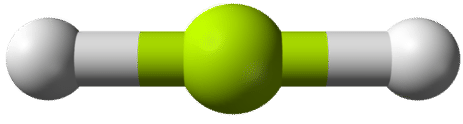
The \(\ce{H-Be-H}\) bond angle is \(180^\text{o}\) because of its linear geometry.
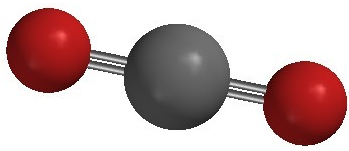
Carbon dioxide is another example of a molecule which falls under the \(\ce{AB_2}\) category. Its Lewis structure consists of double bonds between the central carbon atom and each oxygen atom.
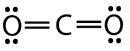
The repulsion between the two double bonds on either side of the carbon atom is no different than the repulsion between the two single bonds on either side of the beryllium in the previous example. Therefore carbon dioxide is also linear, as this achieves the maximum distance between the electron pair bonds.
\(\ce{AB_3}\)
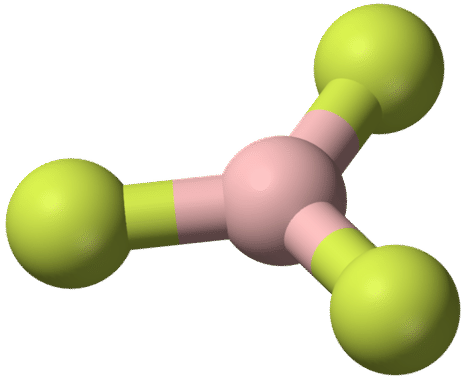
Boron trifluoride \(\left( \ce{BF_3} \right)\) consists of a central boron atom with three single bonds to fluorine atoms. The boron atom is an exception to the octet rule, and generally only needs 6 electrons to be stable in a bonded molecule.
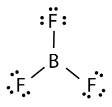
The geometry of the \(\ce{BF_3}\) molecule is called trigonal planar. The fluorine atoms are positioned at the vertices of an equilateral triangle. The \(\ce{F-B-F}\) angle is \(120^\text{o}\), and all four atoms lie in the same plane.
\(\ce{AB_4}\)
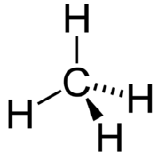
Methane \(\left( \ce{CH_4} \right)\) is an organic compound that is the primary component of natural gas. Its structure consists of a central carbon atom with four single bonds to hydrogen atoms.
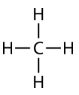
In order to maximize their distance from one another, the four groups of bonding electrons do not lie in the same plane. Instead, each of the hydrogen atoms lies at the corners f a geometrical shape called a tetrahedron. The carbon atom is at the center of the tetrahedron. Each face of a tetrahedron is an equilateral triangle.
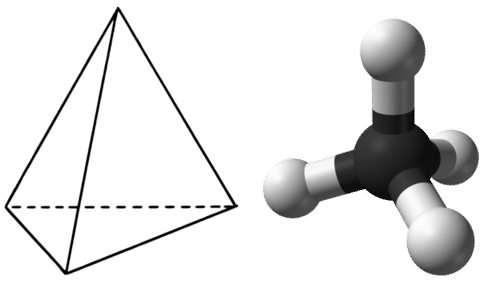
The electron group geometry of the methane molecule is referred to as tetrahedral. The \(\ce{H-C-H}\) bond angles are \(109.5^\text{o}\), which is larger than the \(90^\text{o}\) that they would be if the molecule was planar. This way, the bonds are as far apart as possible to minimize electron repulsion. When drawing a structural formula for a molecule such as methane, it is advantageous to be able to indicate the three-dimensional character of its shape. The structural formula in the figure below is called a perspective drawing. The dotted line bond should be visualized as going back into the page, while the solid triangle bond should be visualized as coming out of the page.
There are structures with five and six bonds that we will not explore because they are not seen in biological molecules.
| Atoms Around Central Atom | Electron Group Geometry | Example |
|---|---|---|
| 2 \(\ce{AB_2}\) | Linear | \(\ce{BeCl_2}\) |
| 3 \(\ce{AB_3}\) | Trigonal Planar | \(\ce{BF_3}\) |
| 4 \(\ce{AB_4}\) | Tetrahedral | \(\ce{CH_4}\) |
Central Atom with One or More Lone Pairs
The number of bonds to the central atom plus the number of lone pairs on the central atom gives us what is called the electron group geometry. Electron group geometries refer to the five geometries: linear, trigonal planar, tetrahedral, trigonal bipyramidal, or octahedral. If one or more of the bonding pairs of electrons is replaced with a lone pair, the electron geometry does not change but the the shape of the molecule is altered. Understanding the impact of lone pairs of electrons will be important when looking at properties of compounds that are affected by polarity of a molecule. We will focus on the tetrahedral electron group geometry since it is most relevant to organic and biological molecules. \(\ce{E}\) represents a non-bonding pair of electrons.
\(\ce{AB_3E}\)
The ammonia molecule contains three single bonds and one lone pair on the central nitrogen atom.
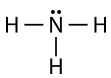
The electron group geometry for a molecule with four electron pairs is tetrahedral, as was seen with \(\ce{CH_4}\). In the ammonia molecule, one of the electron pairs is a lone pair rather than a bonding pair. Although the lone pair is not visible, it will affects the location and bond angles among other atoms in the molecule.
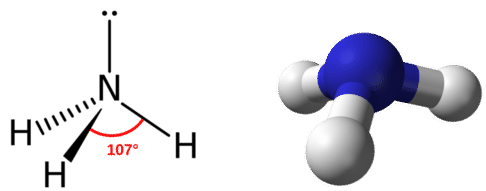
Recall that the bond angles in the tetrahedral \(\ce{CH_4}\) molecule are all equal to \(109.5^\text{o}\). One might expect the \(\ce{H-N-H}\) bond angles in ammonia to be \(109.5^\text{o}\) as well, but slight adjustments need to be made for the presence of lone pairs. Within the context of the VSEPR model, lone pairs of electrons are considered to be slightly more repulsive than bonding pairs of electrons, due to their closer proximity to the central atom. In other words, lone pairs "take up more space". Therefore the \(\ce{H-N-H}\) angle is slightly less than \(109.5^\text{o}\). Its actual value is approximately \(107^\text{o}\).
\(\ce{AB_2E_2}\)
A water molecule consists of two bonding pairs and two lone pairs of electrons.
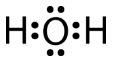
The water molecule, like the ammonia and methane molecules, has a tetrahedral electron group geometry. In the water molecule, two of the electron pairs are lone pairs rather than bonding pairs. The \(\ce{H-O-H}\) bond angle is \(104.5^\text{o}\), which is smaller than the bond angle in \(\ce{NH_3}\).
| Atoms Plus Lone Pairs Around Central Atom | Number of Surrounding Atoms | Number of Lone Pairs | Electron Group Geometry | Example |
|---|---|---|---|---|
| 3 \(\ce{AB_2E}\) | 2 | 1 | Trigonal Planar | \(\ce{O_3}\) |
| 4 \(\ce{AB_3E}\) | 3 | 1 | Tetrahedral | \(\ce{NH_3}\) |
| 4 \(\ce{AB_2E_2}\) | 2 | 2 | Tetrahedral | \(\ce{H_2O}\) |
Contributors and Attributions
Allison Soult, Ph.D. (Department of Chemistry, University of Kentucky)

