2.3: Mole and Molar Mass
- Page ID
- 58795
Learning Outcomes
- Define mole.
- Determine the ratio of elements in a compound from a formula.
- Determine molar mass of an element and compound.
- Convert among mass, moles, and number of particles of a substance.

When you go to the bakery and order a dozen doughnuts, both you and the baker know that means 12. Dozen is a counting number that is defined as 12. There are other counting numbers such as pair (2), ream (500), gross (144), and score (20). The last one was famously used by Abraham Lincoln in the Gettysburg Address when he said "Four score and seven years ago". All of these words define a specific number of things regardless of what it is we are counting. A mole is also a counting number.
Avogadro's Number
It certainly is easy to count bananas or to count elephants (as long as you stay out of their way). However, you would be counting grains of sugar from your sugar canister for a long. long time. Atoms and molecules are extremely small - far, far smaller than grains of sugar. Counting atoms and molecules is not only unwise, it is absolutely impossible. One drop of water contains about \(10^{22}\) molecules of water. If you counted 10 molecules every second for 50 years without stopping you would have counted only \(1.6 \times 10^{10}\) molecules. Put another way, at that counting rate, it would take you over 30 trillion years to count the water molecules in one tiny drop.
Chemists needed a name that can stand for a very large number of items. Amedeo Avogadro (1776 - 1856), an Italian scientist, provided just such a number. He is responsible for the counting unit of measure called the mole. A mole (abbreviated as \(\text{mol}\)) is the amount of a substance that contains \(6.02 \times 10^{23}\) representative particles of that substance. The mole is the SI unit for amount of a substance. Just like dozen or gross, it is a name that stands for a number. There are \(6.02 \times 10^{23}\) atoms in a mole of carbon. There are \(6.02 \times 10^{23}\) water molecules in a mole of water molecules. There also would be \(6.02 \times 10^{23}\) bananas in a mole of bananas, if such a huge number of bananas ever existed.

The number \(6.02 \times 10^{23}\) is called Avogadro's number, the number of representative particles in a mole. It is an experimentally determined number. A representative particle is the smallest unit in which a substance naturally exists. For the majority of elements, the representative particle is the atom. Iron, carbon, and helium consist of iron atoms, carbon atoms, and helium atoms, respectively. Seven elements exist in nature as diatomic molecules and the are \(\ce{H_2}\), \(\ce{N_2}\), \(\ce{O_2}\), \(\ce{F_2}\), \(\ce{Cl_2}\), \(\ce{Br_2}\), and \(\ce{I_2}\). The representative particle for these elements is the molecule. Likewise, all molecular compounds such as \(\ce{H_2O}\) and \(\ce{CO_2}\) exist as molecules and so the molecule is their representative particle. For ionic compounds such as \(\ce{NaCl}\) and \(\ce{Ca(NO_3)_2}\), the representative particle is the formula unit. A mole of any substance contains Avogadro's number \(\left( 6.02 \times 10^{23} \right)\) of representative particles.

Conversions Between Moles and Number of Particles
Using our unit conversion techniques, we can use the mole label to convert back and forth between the number of particles and moles.
Example \(\PageIndex{1}\)
The element carbon exists in two primary forms: graphite and diamond. How many moles of carbon atoms is \(4.72 \times 10^{24}\) atoms of carbon?
Solution
In this problem, we are given the number of atoms and asked to provide the number of moles. We need to determine what factor we will use to convert from atoms to moles. Avogadro's number gives us the relationship we need, \(1 \: \text{mol} = 6.02 \times 10^{23}\) atoms.
\[4.72 \times 10^{24} \: \text{atoms} \: \ce{C} \times \frac{1 \: \text{mol} \: \ce{C}}{6.02 \times 10^{23} \: \text{atoms} \: \ce{C}} = 7.84 \: \text{mol} \: \text{C}\]
Notice that atoms is on the bottom of the conversion factor because we need atoms to cancel so we are left with moles of carbon. Our final check is to make sure our answer is reasonable. Notice that we have \(10^{24}\) atoms of carbon so it is reasonable that the value is greater than 1 mole.
Suppose that you wanted to know how many hydrogen atoms were in a mole of water molecules. First, you would need to know the chemical formula for water, which is \(\ce{H_2O}\). Based on the subscript for hydrogen, there are two atoms of hydrogen in each molecule of water. How many atoms of hydrogen would there be in two water molecules? (see figure below) There would be \(2 \times 2 = 4\) hydrogen atoms. How about in a dozen? In that case a dozen is 12 so \(12 \times 2 = 24\) hydrogen atoms in a dozen water molecules. To get the answers (4 and 24), you had to multiply the given number of molecules by two atoms of hydrogen per molecule. So to find the number of hydrogen atoms in a mole of water molecules, the problem could be solved in a similar manner.
\[1 \: \text{mol} \: \ce{H_2O} \times \frac{6.02 \times 10^{23} \: \text{molecules} \: \ce{H_2O}}{1 \: \text{mol} \: \ce{H_2O}} \times \frac{2 \: \text{atoms} \: \ce{H}}{1 \: \text{molecule} \: \ce{H_2O}} = 1.20 \times 10^{24} \: \text{atoms} \: \ce{H}\]
The first conversion factor converts from moles of particles to the number of particles. The second conversion factor reflects the number of atoms contained within each molecule.
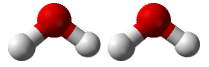
Two water molecules contain 4 hydrogen atoms and 2 oxygen atoms. A mole of water molecules contains 2 moles of hydrogen atoms and 1 mole of oxygen atoms.
Example \(\PageIndex{2}\)
Sulfuric acid has the chemical formula \(\ce{H_2SO_4}\). A certain quantity of sulfuric acid contains \(4.89 \times 10^{25}\) atoms of oxygen. How many moles of sulfuric acid is in the sample?
Solution
In this problem, the number of atoms of oxygen is given. However, the number of molecules of \(\ce{H_2SO_4}\) is not equal to the number of atoms. Therefore, an additional step will be need to solve the problem.
We can write two relationships that will help solve this problem.
- \(1 \: \text{mol} = 6.02 \times 10^{23} \: \text{molecules}\)
- \(1 \: \text{molecule} \: \ce{H_2SO_4} = 4 \: \ce{O} \: \ce{atoms}\)
While 1 mole will always equal \(6.02 \times 10^{23}\), the second relationship will vary depending on the identity of the compound and the element. For \(\ce{H_2SO_4}\), we could also write that 1 molecule of \(\ce{H_2SO_4} = \) 2 atoms \(\ce{H}\) or 1 molecule \(\ce{H_2SO_4} =\) 1 atom \(\ce{S}\). Both of these are true, but they just aren't helpful for this problem.
\[4.89 \times 10^{25} \: \text{atoms} \: \ce{O} \times \frac{1 \: \text{molecule} \: \ce{H_2SO_4}}{4 \: \text{atoms} \: \ce{O}} \times \frac{1 \: \text{mol} \: \ce{H_2SO_4}}{6.02 \times 10^{23} \: \text{molecules} \: \ce{H_2SO_4}} = 20.3 \: \text{mol} \: \ce{H_2SO_4}\]
Note that atoms \(\ce{O}\) and molecules \(\ce{H_2SO_4}\) both cancel and we are left with units of \(\text{mol} \: \ce{H_2SO_4}\).
An alternative way to set up this problem is to use the relationship \(1 \: \text{mol} \: \ce{H_2SO_4} = 4 \: \text{mol} \: \ce{O} \: \text{atoms}\). Since a mole is just a counting number, we are simply multiplying both values (1 molecule and 1 atoms) by Avogadro's number to get a relationship in terms of moles. In this example, we convert from atoms to moles of \(\ce{O}\), then convert from moles of \(\ce{O}\) to moles of \(\ce{H_2SO_4}\).
\[4.89 \times 10^{25} \: \text{atoms} \: \ce{O} \times \frac{1 \: \text{mol} \: \ce{O}}{6.02 \times 10^{23} \: \text{atoms} \: \ce{O}} \times \frac{1 \: \text{mol} \: \ce{H_2SO_4}}{4 \: \text{mol} \: \ce{O}} = 20.3 \: \text{mol} \: \ce{H_2SO_4}\]
Both methods are correct and will give you the same answer. Use the method that makes the most sense to you.
Molar Mass
Molar mass is defined as the mass (in grams) of one mole of representative particles of a substance. By looking at a periodic table, we can conclude that the molar mass of lithium is \(6.94 \: \text{g}\), the molar mass of zinc is \(65.38 \: \text{g}\), and the molar mass of gold is \(196.97 \: \text{g}\). Each of these quantities contains \(6.02 \times 10^{23}\) atoms of that particular element. The units for molar mass are grams per mole or \(\text{g/mol}\). Notice that these are the same numbers as the atomic mass but with different units. For example 1 atom of lithium has a mass of \(6.94 \: \text{amu}\) while 1 mole \(\left( 6.02 \times 10^{23} \: \text{atoms} \right)\) has a mass of \(6.94 \: \text{g}\). We can use this relationship to determine the moles of an element from its mass or vice versa.
Example \(\PageIndex{3}\)
How many moles of carbon are in a \(29.3 \: \text{g}\) sample?
Solution
We are given the mass of the sample and look up the molar mass of carbon in the periodic table which is \(12.01 \: \text{g/mol}\). Now, we can set up the calculation to solve for moles.
\[29.3 \: \text{g} \: \ce{C} \times \frac{1 \: \text{mol} \: \ce{C}}{12.01 \: \text{g} \: \ce{C}} = 2.44 \: \text{mol} \: \ce{C}\]
Note that grams will cancel and we will be left with units of moles of carbon for our answer which is what is being asked for in this problem. Since the mass of the carbon sample is greater than the molar mass, it is reasonable that we have more than one mole of the carbon.
Example \(\PageIndex{4}\)
What is the mass of aluminum in a \(1.95 \: \text{mol}\) sample?
Solution
As in the previous example, we will need the molar mass to solve the problem. For aluminum, the molar mass is \(27.0 \: \text{g/mol}\). Now, we can set up the calculation to solve for mass.
\[1.95 \: \text{mol} \: \ce{Al} \times \frac{27.0 \: \text{g} \: \ce{Al}}{1 \: \text{mol} \: \ce{Al}} = 52.7 \: \text{g} \: \ce{Al}\]
In this example, we put gras on top and moles on the bottom so that the units would cancel correctly. Note that \(\text{mol} \: \ce{Al}\) will cancel and we are left with units of grams of aluminum which is what is being asked for in the problem. The answer looks reasonable because we have almost two moles of aluminum and the mass is almost twice the molar mass.
Molar Masses of Compounds
The molecular formula of the compound carbon dioxide is \(\ce{CO_2}\). One molecule of carbon dioxide consists of 1 atom of carbon and 2 atoms of oxygen. We can calculate the mass of one molecule of carbon dioxide by adding together the masses of 1 atom of carbon and 2 atoms of oxygen.
\[12.01 \: \text{amu} + 2 \left( 16.00 \: \text{amu} \right) = 44.01 \: \text{amu}\]
The molecular mass of a compound is the mass of one molecule of that compound. The molecular mass of carbon dioxide is \(44.01 \: \text{amu}\).
The molar mass of any compound is the mass in grams of one mole of that compound. One mole of carbon dioxide molecules has a mass of \(44.01 \: \text{g}\). The molar mass is \(44.01 \: \text{g/mol}\) for \(\ce{CO_2}\). For water, the molar mass is \(18.02 \: \text{g/mol}\). In both cases, it is the mass of \(6.02 \times 10^{23}\) molecules.
Example \(\PageIndex{5}\)
Calcium nitrate, \(\ce{Ca(NO_3)_2}\), is used as a component in fertilizer. Determine the molar mass of calcium nitrate.
Solution
The molar mass of a compound is found from the molar masses of the elements in the compound.
- \(\ce{Ca} = 40.08 \: \text{g/mol}\)
- \(\ce{N} = 14.01 \: \text{g/mol}\)
- \(\ce{O} = 16.00 \: \text{g/mol}\)
First we need to analyze the formula. Since the \(\ce{Ca}\) lacks a subscript, there is one \(\ce{Ca}\) atom per formula unit. The 2 outside the parentheses means that there are two nitrate ions per formula unit and each nitrate ion consist of one nitrogen atom and three oxygen atoms. Therefore, there are a total of \(1 \times 2 = 2\) nitrogen atoms and \(3 \times 2 = 6\) oxygen atoms per formula unit. Thus, \(1 \: \text{mol}\) of calcium nitrate contains \(1 \: \text{mol}\) of \(\ce{Ca}\) atoms, \(2 \: \text{mol}\) of \(\ce{N}\) atoms, and \(6 \: \text{mol}\) of \(\ce{O}\) atoms.
Use the molar masses of each atom together with the number of atoms in the formula and add together.
\[\begin{align} &1 \: \text{mol} \: \ce{Ca} \times \frac{40.08 \: \text{g} \: \ce{Ca}}{1 \: \text{mol} \: \ce{Ca}} = 40.08 \: \text{g} \: \ce{Ca} \\ &2 \: \text{mol} \: \ce{N} \times \frac{14.01 \: \text{g} \: \ce{N}}{1 \: \text{mol} \: \ce{N}} = 28.02 \: \text{g} \: \ce{N} \\ &6 \: \text{mol} \: \ce{O} \times \frac{16.00 \: \text{g} \: \ce{O}}{1 \: \text{mol} \: \ce{O}} = 96.00 \: \text{g} \: \ce{O} \\ &\text{molar mass of} \ce{Ca(NO_3)_2} = 40.08 \: \text{g} + 28.02 \: \text{g} + 96.00 \: \text{g} = 164.10 \: \text{g/mol} \end{align}\]
Conversions Between Moles and Mass
Like we converted between moles and mass of an element, we can also convert between moles and mass of a compound using the molar mass of the compound. This relationship is frequently used in the laboratory. Suppose that for a certain experiment you need 3.00 moles of calcium chloride \(\left( \ce{CaCl_2} \right)\). Since calcium chloride is a solid, it would be convenient to use a balance to measure the mass that is needed. The molar mass of \(\ce{CaCl_2}\) is \(110.98 \: \text{g/mol}\). The relationship that can be used is then based on the equality that \(1 \: \text{mol} = 110.98 \: \text{g} \: \ce{CaCl_2}\). Dimensional analysis will allow you to calculate the mass of \(\ce{CaCl_2}\) that you should measure.
\[3.00 \: \text{mol} \: \ce{CaCl_2} \times \frac{110.98 \: \text{g} \: \ce{CaCl_2}}{1 \: \text{mol} \: \ce{CaCl_2}} = 333 \: \text{g} \: \ce{CaCl_2}\]
When you measure the mass of \(333 \: \text{g}\) of \(\ce{CaCl_2}\), you are measuring 3.00 moles of \(\ce{CaCl_2}\).

Calcium chloride is used as a drying agent and as a road deicer.
Example \(\PageIndex{6}\)
A certain reaction produces \(2.81 \: \text{g}\) of copper (II) hydroxide, \(\ce{Cu(OH)_2}\). Determine the number of moles produced in the reaction.
Solution
The mass of the substance is known and we can determine the moles using the molar mass of the compound, \(\ce{Cu(OH)_2}\). First we have to find the molar mass of \(\ce{Cu(OH)_2}\) using the molar masses of the elements.
\[\text{molar mass} \: \ce{Cu(OH)_2} = 63.55 \: \text{g/mol} + 2 \left( 16.00 \: \text{g/mol} \right) + 2 \left( 1.008 \: \text{g/mol} \right) = 97.57 \: \text{g/mol}\]
Now, we can use the molar mass to convert from grams to moles.
\[2.81 \: \text{g} \: \ce{Cu(OH)_2} \times \frac{1 \: \text{mol} \: \ce{Cu(OH)_2}}{97.57 \: \text{g} \: \ce{Cu(OH)_2}} = 0.0288 \: \text{mol} \: \ce{Cu(OH)_2}\]
The units of grams will cancel and we are left with units of moles which is what is being requested in the question.
Example \(\PageIndex{7}\)
What is the mass of water in a \(3.50 \: \text{mol}\) sample?
Solution
In this example, the moles of water is known and we need to find the mass. Again, we will use the molar mass which was previously given as \(18.02 \: \text{g/mol}\).
\[3.50 \: \text{mol} \: \ce{H_2O} \times \frac{18.02 \: \text{g} \: \ce{H_2O}}{1 \: \text{mol} \: \ce{H_2O}} = 63.1 \: \text{g} \: \ce{H_2O}\]
The units of \(\text{mol} \: \ce{H_2O}\) will cancel and we are left with units of grams which is what is being requested in the question.
Supplemental Resources
- Molar Mass Problems: http://misterguch.brinkster.net/molarmass.html
Contributors and Attributions
Allison Soult, Ph.D. (Department of Chemistry, University of Kentucky)

