10.3: Half-Life
- Page ID
- 58838
Learning Outcomes
- Define half-life as it relates to radioactive nuclides and solve half-life problems.
- Describe the general process by which radioactive dating is used to determine the age of various objects.
- Calculate the time for a sample to decay.
- Complete dosage calculations based on nuclide activity.
The rate of radioactive decay is often characterized by the half-life of a radioisotope. Half-life \(\left( t_{1/2} \right)\) is the time required for one half of the nuclei in a sample of radioactive material to decay. After each half-life has passed, one half of the radioactive nuclei will have transformed into a new nuclide (see table below). The rate of decay and the half-life do not depend on the original size of the sample. They also do not depend upon environmental factors such as temperature and pressure.
| Number of Half-Lives Passed | Fraction Remaining | Percentage Remaining | Mass remaining starting with \(80 \: \text{g}\) |
|---|---|---|---|
| 1 | 1/2 | 50 | \(40 \: \text{g}\) |
| 2 | 1/4 | 25 | \(20 \: \text{g}\) |
| 3 | 1/8 | 12.5 | \(10 \: \text{g}\) |
| 4 | 1/16 | 6.25 | \(5.0 \: \text{g}\) |
| 5 | 1/32 | 3.125 | \(2.5 \: \text{g}\) |
As an example, iodine-131 is a radioisotope with a half-life of 8 days. It decays by beta particle emission into xenon-131.
\[\ce{^{131}_{53}I} \rightarrow \ce{^{131}_{54}Xe} + \ce{^0_{-1}e}\]
After eight days have passed, half of the atoms of any sample of iodine-131 will have decayed, and the sample will now be \(50\%\) iodine-131 and \(50\%\) xenon-131. After another eight days pass (a total of 16 days or 2 half-lives), the sample will be \(25\%\) iodine-131 and \(75\%\) xenon-131. This continues until the entire sample of iodine-131. has completely decayed (see figure below).
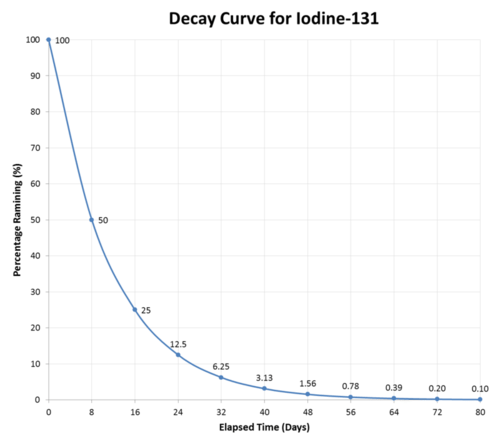
Half-lives have a very wide range, from billions of years to fractions of a second. Listed below (see table below) are the half-lives of some common and important radioisotopes. Those with half-lives on the scale of hours or days are the ones most suitable for use in medical treatment.
The following example illustrates how to use the half-life of a sample to determine the amount of radioisotope that remains after a certain period of time has passed.
Example \(\PageIndex{1}\): Strontium-90
Strontium-90 has a half-life of 28.1 days. If you start with a \(5.00 \: \text{mg}\) sample of the isotope, how much remains after 140.5 days have passed?
Solution
Step 1: List the known values and plan the problem.
Known
- Original mass \(= 5.00 \: \text{mg}\)
- \(t_{1/2} =\) 28.1 days
- Time elapsed \(=\) 140.5 days
Unknown
- Final mass of \(\ce{Sr}\)-90 \(= ? \: \text{mg}\)
First, find the number of half-lives that have passed by dividing the time elapsed by the half-life. Then, reduce the amount of \(\ce{Sr}\)-90 by half, once for each half-life.
Step 2: Solve.
Number of half-lives, days, mass
0 half-lives, 0 days, \(5.00 \: \text{mg}\)
1 half-life, 28.1 days, \(2.50 \: \text{mg}\)
2 half-lives, 56.2 days, \(1.25 \: \text{mg}\)
3 half-lives, 84.3 days, \(0.613 \: \text{mg}\)
4 half-lives, 112.4 days, \(0.313 \: \text{mg}\)
5 half-lives, 140.5 days, \(0.156 \: \text{mg}\)
Step 3: Think about your result.
According to the data above, the passage of 5 half-lives means \(0.156 \: \text{mg}\) of the original \(\ce{Sr}\)-90 remains. The remaining \(4.844 \: \text{mg}\) has decayed by beta particle emission to yttrium-90.
Radioactive Dating
Radioactive dating is a process by which the approximate age of an object is determined through the use of certain radioactive nuclides. For example, carbon-14 has a half-life of 5,730 years and is used to measure the age of organic material. The ratio of carbon-14 to carbon-12 in living things remains constant while the organism is alive because fresh carbon-14 is entering the organism whenever it consumes nutrients. When the organism dies, this consumption stops, and no new carbon-14 is added to the organism. As time goes by, the ratio of carbon-14 to carbon-12 in the organism gradually declines, because carbon-14 radioactively decays while carbon-12 is stable. Analysis of this ratio allows archaeologists to estimate the age of organisms that were alive many thousands of years ago. Carbon dating is effective until about 50,000 years. The ages of many rocks and minerals are far greater than the ages of fossils. Uranium-containing minerals that have been analyzed in a similar way have allowed scientists to determine that the Earth is over 4 billion years old.
Decay Series
In many instances, the decay of an unstable radioactive nuclide simply produces another radioactive nuclide. It may take several successive steps to reach a nuclide that is stable. A decay series is a sequence of successive radioactive decays that proceeds until a stable nuclide is reached. The terms reactant and product are generally not used for nuclear reactions. Instead, the terms parent and daugher nuclide are used to to refer to the starting and ending isotopes in a decay process. The figure below shows the decay series for uranium-238.
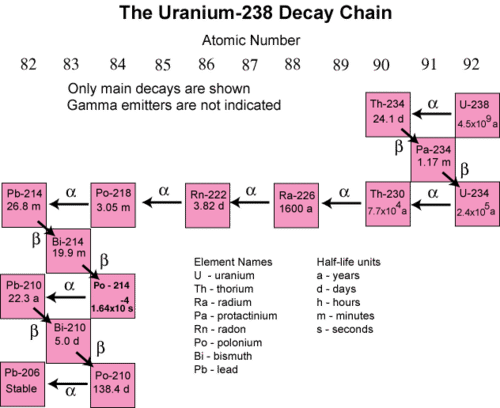
In the first step, uranium-238 decays by alpha emission to thorium-234 with a half-life of \(4.5 \times 10^9\) years. This decreases its atomic number by two. The thorium-234 rapidly decays by beta emission to protactinium-234 (\(t_{1/2} =\) 24.1 days). The atomic number increases by one. This continues for many more steps until eventually the series ends with the formation of the stable isotope lead-206.
Artificial Transmutation
As we have seen, transmutation occurs when atoms of one element spontaneously decay and are converted to atoms of another element. Artificial transmutation is the bombardment of stable nuclei with charged or uncharged particles in order to cause a nuclear reaction. The bombarding particles can be protons, neutrons, alpha particles, or larger atoms. Ernest Rutherford performed some of the earliest bombardments, including the bombardment of nitrogen gas with alpha particles to produce the unstable fluorine-18 isotope.
\[\ce{^{14}_7N} + \ce{^4_2He} \rightarrow \ce{^{18}_9F}\]
Fluorine-18 quickly decays to the stable nuclide oxygen-17 by releasing a proton.
\[\ce{^{18}_9F} \rightarrow \ce{^{17}_8O} + \ce{^1_1H}\]
When beryllium-9 is bombarded with alpha particles, carbon-12 is produced with the release of a neutron.
\[\ce{^9_4Be} + \ce{^4_2He} \rightarrow \ce{^{12}_6C} + \ce{^1_0n}\]
Transuranium Elements
Many, many radioisotopes that do not occur naturally have been generated by artificial transmutation. The elements technetium and promethium have been produced, since these elements no longer occur in nature. All of their isotopes are radioactive and have half-lives short enough that any amount of the elements that once existed have long since disappeared through natural decay. The transuranium elements are elements with atomic numbers greater than 92. All isotopes of these elements are radioactive and none occur naturally.
Dosing
Half-life calculations can be based on mass, percent remaining, or dose. Regardless of which one, the concept is still the same. Understanding the radioactivity and half-life of a sample is important for calculating the correct dose for a patient and determining the levels and duration of radioactive emission from a patient after treatment is received.
Frequently, dosages for radioactive isotopes are given the activity in volume. For example, the concentration of \(\ce{I}\)-137 is given as \(50 \: \mu \text{Ci/mL}\) (microCurie per milliliter). This relationship can be used to calculate the volume needed for a particular dose. For example, a patient needs \(125 \: \mu \text{Ci}\) of \(\ce{I}\)1-51. What volume of a \(50 \mu \text{Ci}\) per \(10 \: \text{mL}\) solution should be given?
\[125 \: \mu \text{Ci} \left( \frac{10 \: \text{mL}}{50 \: \mu \text{Ci}} \right) = 25 \: \text{mL}\]
Example \(\PageIndex{2}\)
A patient is given \(\ce{I}\)-131 to treat thyroid cancer. The patient receives \(5.50 \: \text{mL}\) of a solution containing \(50 \: \text{mCi}\) (milliCurie) in \(2 \: \text{mL}\) (assume concentration is an exact number). What does (in \(\text{mCi}\)) is given to the patient? What will be the activity in \(\text{mCi}\) after 24.21 days given that the half-life of \(\ce{I}\)-131 is 8.07 days?
Solution
The first part of the problem is to find the dose given to the patient. We are given the volume and the concentration (in units of radioactivity over volume).
\[5.50 \: \text{mL solution} \left( \frac{50 \: \text{mCi}}{2 \: \text{mL}} \right) = 138 \: \text{mCi}\]
The patient is given a does of \(138 \: \text{mCi}\).
Now, we need to find the activity after 24.21 days have passed. After one half-life (8.07 days), the sample will have half as much activity \(\left( 138/2 = 69.0 \: \text{mCi} \right)\). After two half-lives (total of 16.14 days), the sample will have half as much activity as after the first half-life \(\left( 69.0/2 = 34.5 \: \text{mCi} \right)\). After three half-lives (total of 24.21 days), the sample will have half as much activity as after the second half-life \(\left( 34.5/2 = 17.3 \: \text{mCi} \right)\). Therefore, after 24.21 days (3 half-lives), the radioactivity will be \(17.3 \: \text{mCi}\).
Contributors and Attributions
Allison Soult, Ph.D. (Department of Chemistry, University of Kentucky)

