1.3: Scientific Dimensional Analysis

Learning Outcomes

• Convert values among units.
• Use dimensional analysis to solve problems.

Dimensional analysis (also called factor label method or unit analysis) is used to convert from one set of units to another. This method is used for both simple (feet to inches) and complex (\(\text{g/cm}^3\) to \(\text{kg}\)/gallon) conversions and uses relationships or conversion factors between different sets of units. While the terms are frequently used interchangeably, conversion factors and relationships are different. Conversion factors are quantities that are equal to one another, such as \(100 \: \text{cm} = 1 \: \text{m}\), in which both values describe a length. Relationships are between two values that are not necessarily a measure of the same quantity. For example, the density of water is \(1.00 \: \text{g/mL}\). Grams are a measure of mass while milliliters measure volume so this is considered a relationship rather than a conversion factor. Either way, we depend on units to help set up and solve the calculation. We will see additional examples of relationships as we explore other details about chemical substance.

Importance of using Correct Conversions

In healthcare professions, a calculation error can quite literally have a life or death consequence. Read the short article, Med-Math Errors and the Nursing Student at http://www.alysion.org/dimensional/matherrors.htm, to better understand the importance of units and correct calculations.

Conversion Factors

Many quantities can be expressed in several different ways. The English system measurement of 4 cups is also equal to 2 pints, 1 quart, and \(\ce{1/4}\) of a gallon. \(4 \: \text{cups} = 2 \: \text{pints} = 1 \: \text{quart} = 0.25 \: \text{gallon}\). Notice that the numerical component of each quantity is different, while the actual amount of material that it represents is the same. That is because the units are different. We can establish the same set of equalities for the metric system: \(1 \: \text{meter} = 10 \: \text{decimeters} = 100 \: \text{centimeters} = 1000 \: \text{millimeters}\). The metric system's use of powers of 10 for all conversions makes this quite simple. We can write conversion factors between any pair of equivalent quantities. In each conversion factor, the numerator and denominator represent equal quantities so they are all valid conversion factors. Additionally, these conversion factors can be inverted or used in combination with other conversion factors in a dimensional analysis problem.

\[ \dfrac{\text{4 cups}}{\text{2 pints}} =\dfrac{\text{1 quart}}{\text{4 cups}} = \dfrac{\text{0.25 gallen}}{\text{1 quarter}}=1 \nonumber\]

\[ \dfrac{\text{1 meter}}{\text{10 decimeters}} =\dfrac{\text{100 centimeters}}{\text{1000 milimeters}} = \dfrac{\text{1000 milimeters}}{\text{1 meter}}=1 \nonumber\]

Example \(\PageIndex{1}\)

How many centimeters are in \(3.4 \: \text{m}\)?

Solution

This problem requires the conversion from one unit to another so we can use dimensional analysis to solve the problem. We need to identify the units that are given \(\left( \text{m} \right)\), the units for the answer \(\left( \text{cm} \right)\), and any relationships that relate the units of the known and unknown values. In this case, we will use the relationship of \(1 \: \text{m} = 100 \: \text{cm}\). Start with the known value and its unit.

\[3.4 \: \text{m} \times \dfrac{?}{?} \nonumber\]

Then, we look at the units of our relationship to see which value goes in the numerator and which value goes in the denominator. Remember, we are trying to find the value in centimeters. Since our known value is in units of meters, we need meters to be in the denominator so that it will cancel. As a result, centimeters will be in the numerator.

\[3.4 \: \text{m} \times \dfrac{100 \: \text{cm}}{1 \: \text{m}} \nonumber\]

Note that the numbers stay with the appropriate unit (100 with centimeters and 1 with meters). Now, the meters will cancel out and we are left with units of centimeters. Always check that your problem is set up completely and that your units cancel correctly before you do the actual calculation.

\[\begin{align*}3.4 \: \cancel{\text{m}} \times \dfrac{100 \: \text{cm}}{1 \: \cancel{\text{m}}} &= 340 \: \text{cm} \\[5pt] &= 3.4 \times 10^2 \: \text{cm} \end{align*}\]

We find the answer to be \(340 \: \text{cm}\) or \(3.4 \times 10^2 \: \text{cm}\).

Derived Units

Using dimensional analysis with derived units requires special care. When units are squared or cubed as with area or volume, the conversion factors themselves must also be squared or cubed. Two convenient volume units are the liter, which is equal to a cubic decimeter, and the milliliters, which is equal to a cubic centimeter. There are thus \(1000 \: \text{cm}^3\) in \(1 \: \text{dm}^3\), which is the same thing as saying there are \(1000 \: \text{mL}\) in \(1 \: \text{L}\). The conversion factor of \(1 \: \text{cm}^3 = 1 \: \text{mL}\) is a very useful conversion.

Figure \(\PageIndex{1}\): One centimeter cubed is the volume occupied by a cube with an edge length of \(1 \: \text{cm}\).

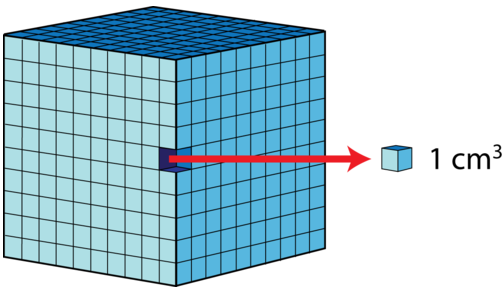
There are \(1000 \: \text{cm}^3\) in \(1 \: \text{dm}^3\). Since a \(\text{cm}^3\) is equal to a \(\text{mL}\), and a \(\text{dm}^3\) is equal to a \(\text{L}\), we can say that there are \(1000 \: \text{mL}\) in \(1 \: \text{L}\).

Example \(\PageIndex{2}\)

Convert \(3.6 \: \text{mm}^3\) to \(\text{mL}\).

Solution

Determine the units of the known value \(\left( \text{mm}^3 \right)\) and the units of the unknown value \(\left( \text{mL} \right)\). The starting and ending units will help guide the setup of the problem. Next, list any known conversion factors that might be helpful.

• \(1 \: \text{m} = 1000 \: \text{mm}\)
• \(1 \: \text{mL} = 1 \: \text{cm}^3\)
• \(1 \: \text{m} = 100 \: \text{cm}\)

Now, we can set up the problem to find the value in units of \(\text{mL}\). Once we know the starting units, we can then use the conversion factors to find the answer.

\[3.6 \: \text{mm}^3 \times \left( \dfrac{?}{?} \right) \nonumber\]

Continue to use the conversion factors between the units to set up the rest of the problem. Note that all of the units cancel except \(\text{mL}\), which are the requested units for the answer. Since the values in these conversion factors are exact numbers, they will not affect the number of significant figures in the answer. Only the original value (3.6) will be considered in determining significant figures.

\[3.6 \: \text{mm}^3 \times \left( \dfrac{1 \: \text{m}}{1000 \: \text{mm}} \right)^3 \times \left( \dfrac{?}{?} \right) \nonumber\]

Once you have solved the problem, always ask if the answer seems reasonable. Remember, a millimeter is very small and a cubic millimeter is also very small. Therefore, we would expect a small volume which means \(0.0036 \: \text{mL}\) is reasonable.

If you find that you forgot to cube numbers as well as units, you can setup the problem in an expanded form which is the equivalent to the previous method to cube the numerical values.

Contributors and Attributions

• Allison Soult, Ph.D. (Department of Chemistry, University of Kentucky)