1.2: Significant Figures
- Page ID
- 84282
Learning Outcomes
- Distinguish between accuracy and precision.
- Explain the concept of significant figures.
- Report answers to calculations with the correct number of significant figures.
In chemistry, we are looking at measurements and not just numbers. Therefore, it is necessary to be able to count the number of significant figures and report measurements to the correct level of precision. The reported value should be as precise as possible without adding digits to a value that cannot be measured.
Accuracy and Precision
In everyday speech, the terms accuracy and precision are frequently used interchangeably. However, their scientific meanings are quite different. Accuracy is a measure of how close a measurement is to the correct or accepted value of the quantity being measured. Precision is a measure of how close a series of measurements are to one another. Precise measurements are highly reproducible, even if the measurements are not near the correct value. Darts thrown at a dartboard are helpful in illustrating accuracy and precision (see figure below).
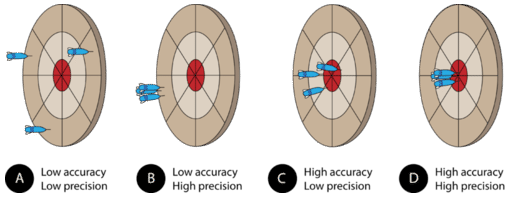
Assume that three darts are thrown at the dartboard, with the bulls-eye representing the true, or accepted, value of what is being measured. A dart that hits the bulls-eye is highly accurate, whereas a dart that lands far away from the bulls-eye displays poor accuracy. Pictured above are the four possible outcomes.
(A) The darts have landed far from each other and far from the bulls-eye. This grouping demonstrates measurements that are neither accurate nor precise.
(B) The darts are close to one another, but far from the bulls-eye. This grouping demonstrates measurements that are precise, but not accurate. In a laboratory situation, high precision with low accuracy often results from a systematic error. Either the measurer makes the same mistake repeatedly or the measuring tool is somehow flawed. A poorly calibrated balance may give the same mass reading every time, but it will be far from the true mass of the object.
(C) The darts are not grouped very near to each other, but they are generally centered around the bulls-eye. This demonstrates poor precision but fairly high accuracy. This situation is not desirable because in a lab situation, we do not know where the "bulls-eye" actually is. Continuing with this analogy, measurements are taken in order to find the bulls-eye. If we could only see the locations of the darts and not the bulls-eye, the large spread would make it difficult to be confident about where the exact center was, even if we knew that the darts were thrown accurately (which would correspond to having equipment that is calibrated and operated correctly).
(D) The darts are grouped together and have hit the bulls-eye. This demonstrates high precision and high accuracy. Scientists always strive to maximize both in their measurements. Turning back to our laboratory situation, where we can see the darts but not the bulls-eye, we have a much narrower range of possibilities for the exact center than in the less precise situation depicted in part C.
Significant Figures in Measurements
Some error or uncertainty always exists in any measurement. The amount of uncertainty depends both upon the skill of the measurer and upon the quality of the measuring tool. While some balances are capable of measuring masses only to the nearest \(0.1 \: \text{g}\), other highly sensitive balances are capable of measuring to the nearest \(0.001 \: \text{g}\) or even better. Many measuring tools such as rulers and graduated cylinders have small lines which need to be carefully read in order to make a measurement. Pictured below is an object (indicated by the blue arrow) whose length is being measured by two different rulers.
With either ruler, it is clear that the length of the object is between 2 and 3 centimeters. The bottom ruler contains no millimeter markings, so the tenths digit can only be estimated, and the length may be reported by one observer as \(2.5 \: \text{cm}\). However, another person may judge that the measurement is \(2.4 \: \text{cm}\) or perhaps \(2.6 \: \text{cm}\). While the 2 is known for certain, the value of the tenths digit is uncertain.
The top ruler contains marks for tenths of a centimeter (millimeters). Now, the same object may be measured as \(2.55 \: \text{cm}\). The measurer is capable of estimating the hundredths digit because he can be certain that the tenths digit is a 5.
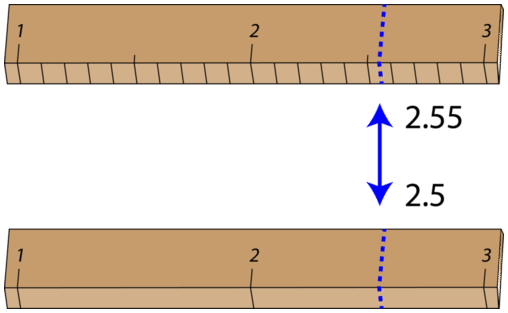
Again, another measurer may report the length to be \(2.54 \: \text{cm}\) or \(2.66 \: \text{cm}\). In this case, there are two certain digits (the 2 and the 5), with the hundredths digit being uncertain. Clearly, the top ruler is a superior ruler for measuring lengths as precisely as possible.
The significant figures in a measurement consist of all the certain digits in that measurement plus one uncertain (estimated) digit. In a correctly reported measurement, the final digit is significant but not certain. Insignificant digits are not reported.
Rules for Determination of Significant Figures
1. All nonzero digits are significant.
- 237 has three significant figures
- 1.897 has four significant figures
2. Zeroes between significant figures are significant.
- 39004 has five significant figures
- 2.03 has three significant figures
3. Zeroes that appear to the left of all of the nonzero digits are called placeholder zeroes and are not significant.
- 0.008 has one significant figure
- 0.0000416 has three significant figures
4. Zeroes that appear after the last nonzero digit may be significant.
a. If the number is greater than 1 and the zero(es) are not followed by a decimal point, then the number of significant figures is ambiguous.
- 140 is ambiguous
b. If the zero is followed by a decimal point, then the zero is significant.
- 140. has three significant figures (note the decimal point after the zero)
c. If the zero is after a decimal point, then the zero is significant.
- 141.0 has four significant figures
It needs to be emphasized that just because a certain digit is not significant does not mean that it is not important or that it can be left out. Though the zero in a measurement of 140 may not be significant, the value cannot simply be reported as 14. An insignificant zero functions as a placeholder for the decimal point. When numbers are written in scientific notation, this becomes more apparent. The measurement 140 can be written as \(1.4 \times 10^2\), with two significant figures in the coefficient or as \(1.40 \times 10^3\), with three significant figures. A number less than one, such as 0.000416, can be written in scientific notation as \(4.16 \times 10^{-4}\), which has 3 significant figures. In some cases, scientific notation is the only way to correctly indicate the correct number of significant figures. In order to report a value of 15,000,00 with four significant figures, it would need to be written as \(1.500 \times 10^7\).
Exact Quantities
When numbers are known exactly, the significant figure rules do not apply. This occurs when objects are counted rather than measured. For example, a carton of eggs has 12 eggs. The actual value cannot be 11.8 eggs, since we count eggs in whole number quantities. So the 12 is an exact quantity. Exact quantities are considered to have an infinite number of significant figures; the importance of this concept will be seen later when we begin looking at how significant figures are dealt with during calculations. Numbers in many conversion factors, especially for simple unit conversions, are also exact quantities and have infinite significant figures. There are exactly 100 centimeters in 1 meter and exactly 60 seconds in 1 minute. Those values are definitions and are not the result of a measurement.
Calculations
Adding and Subtracting Significant Figures
The sum or difference is determined by the smallest number of digits to the right of the decimal point in any of the original numbers.
Example \(\PageIndex{1}\)
What is the result of \(89.332 + 1.1\) when answered to the correct number of significant figures?
Solution
The mathematical result is \(89.332 + 1.1 = 90.432\). However, we need to round the answer to the correct number of significant figures. For addition and subtraction, the answer should have the same number of decimal places as the starting value with the least number of decimal places. Since 1.1 only has one digit after the decimal place, the answer will be rounded to one decimal place. The first digit to be dropped is less than five so we round down.
The correct answer is 90.4.
Multiplying and Dividing Significant Figures
The number of significant figures in the final product or quotient is equal to the number of significant figures in the starting value that has the fewest significant figures.
Example \(\PageIndex{2}\)
What is the product of 2.8 and 4.5039 reported to the correct number of significant figures?
Solution
First, we find the mathematical answer to the calculation which is \(2.8 \times 4.5039 = 12.61092\). Next, we need to round the answer to the correct number of significant figures. For multiplication and division, the answer should be rounded to that it has the same number of significant figures as the starting value with the least number of significant figures. The value 2.8 has two significant figures while 4.5039 has five. Therefore, the answer should have two significant figures so we should round the answer to 13 because the first digit to be dropped is greater than 5, so we need to round up.
Example \(\PageIndex{3}\)
A bag of chocolate candies has a mass of 8.25 ounces. The candies were to be divided among 4 people. How many ounces should each person get? Report your answer to the correct number of significant figures.
Solution
First, we'll find the mathematical answer to this calculation: \(8.25 \div 4 = 2.0625\). Now, we need to round to the correct number of significant figures so we look back at the starting values. There are three significant figures in 8.25 but 4 is an exact number so it is not considered when determining the number of significant figures in the answer. Therefore, the answer should be rounded to three significant figures or 2.06 ounces.
Supplemental Resources
Contributors and Attributions
Allison Soult, Ph.D. (Department of Chemistry, University of Kentucky)

