1.1: Measurements Matter
- Page ID
- 58481
Learning Outcomes
- Demonstrate use of scientific notation.
- Identify base and derived units for measurements.
- Memorize the metric prefixes, abbreviations, and values (Tables 1.1.1 and 1.1.3).
- Convert between temperatures in Celsius and Fahrenheit.
Many aspects of chemistry use quantitative measurements to describe behavior. In this section, we will look at how we deal with very large or very small numbers, units of measure and prefixes used with these units, and how numbers are reported.
Scientific Notation
Scientific notation is a way to express numbers as the product of two numbers: a coefficient and the number 10 raised to a power. It is a very useful tool for working with numbers that are either very large or very small. As an example, the distance from Earth to the Sun is about 150,000,000,000 meters - a very large distance indeed. In scientific notation, the distance is written as \(1.5 \times 10^{11} \: \text{m}\). The coefficient is the 1.5 and must be a number greater than or equal to 1 and less than 10. The power of 10, or exponent, is 11 because you would have to multiply 1.5 by \(10^{11}\) to get the correct number. Scientific notation is sometimes referred to as exponential notation.
When working with small numbers, we use a negative exponent. So 0.1 meters is \(1 \times 10^{-1}\) meters, 0.01 is \(1 \times 10^{-2}\) and so forth. A red blood cell has a diameter of 0.000008 meters which is neither convenient to write nor say. It is much easier to report a diameter of \(8 \times 10^{-6} \: \text{m}\). Using scientific notation is one way to make writing very large or very small numbers more convenient. Note the use of a leading zero (the zero to the left of the decimal point) when writing very small numbers. The leading zero is there to help you see the decimal point more clearly. The figure 0.01 is less likely to be misunderstood that .01 where you may not see the decimal point.
Units
SI Base Units
All measurements depend on the use of units that are all well known and understood. The English system of measurement units (inches, feet, ounces, etc.) are not used in science because of the difficulty in converting from one unit to another. The metric system is used because all metric units are based on multiples of 10, making conversions very simple. The metric system was originally established in France in 1795. The International System of Units is a system of measurement based on the metric system. The acronym SI is commonly used to refer to this system and stands for the French term, Le Système International d'Unités. The SI was adopted by international agreement in 1960 and is composed of seven base units, five of which are shown in the table below. While some of the base units have a calculation as their standard, the kilogram has a physical standard but there is a movement to change that. Read or listen to more about changes to the standard at http://www.npr.org/templates/story/s...ryId=112003322.
| Quantity | SI Base Unit | Symbol |
|---|---|---|
| Length | meter | \(\text{m}\) |
| Mass | kilogram | \(\text{kg}\) |
| Temperature | kelvin | \(\text{K}\) |
| Time | second | \(\text{s}\) |
| Amount of a Substance | mole | \(\text{mol}\) |
These five units are frequently encountered in chemistry and other units of measurement, such as volume, force, and energy, can be derived from the SI base units.

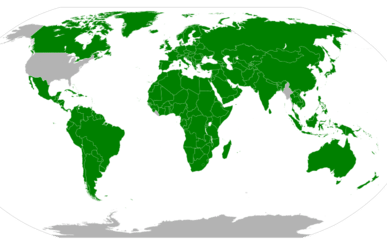
The map in the figure below shows the adoption of the SI units in countries around the world. The United States has legally adopted the metric system for measurements, but does not use it in everyday practice. Great Britain and much of Canada use a combination of metric and imperial units.
Derived Units
Some units are combinations of SI base units. A derived unit is a unit that results from a mathematical combination of SI base units. These derived units are the standard for these quantities but they are not always the units used in normal practice. For example, the density of a solid or a liquid is often reported as \(\text{g/cm}^3\), or \(\text{g/mL}\) rather than \(\text{kg/m}^3\) (the derived SI unit). Some common examples of derived units are listed in the table below.
| Quantity | Symbol | Unit | Unit Abbreviation | Derivation |
|---|---|---|---|---|
| Area | \(A\) | square meter | \(\text{m}^2\) | \(\text{length} \times \text{width}\) |
| Volume | \(V\) | cubic meter | \(\text{m}^3\) | \(\text{length} \times \text{width} \times \text{height}\) |
| Density | \(D\) | kilograms/cubic meter | \(\text{kg/m}^3\) | \(\frac{\text{mass}}{\text{volume}}\) |
| Concentration | \(c\) | moles/liter | \(\text{mol/L}\) | \(\frac{\text{amount}}{\text{volume}}\) |
| Speed (velocity) | \(v\) | meters/second | \(\text{m/s}\) | \(\frac{\text{length}}{\text{time}}\) |
| Acceleration | \(a\) | meters/second/second | \(\text{m/s}^2\) | \(\frac{\text{speed}}{\text{time}}\) |
| Force | \(F\) | newton | \(\text{N}\) | \(\text{mass} \times \text{acceleration}\) |
| Energy | \(E\) | joule | \(\text{J}\) | \(\text{force} \times \text{length}\) |
Metric Prefixes
Conversions between metric system units are straightforward because the system is based on powers of ten. For example, meters, centimeters, and millimeters are all metric units of length. There are 10 millimeters in 1 centimeter and 100 centimeters in 1 meter. Metric prefixes are used to distinguish between units of different size. These prefixes all derive from either Latin or Greek terms. For example, mega comes from the Greek word \(\mu \epsilon \gamma \alpha \varsigma\), meaning "great".
The table below lists the most common metric prefixes and their relationship to the base unit that has no prefix. Length is used as an example to demonstrate the relative size of each prefixed unit. However, these prefixes can be used with any base unit.
| Prefix | Unit Abbreviation | Meaning | Example |
|---|---|---|---|
| giga | \(\text{G}\) | 1,000,000,000 | 1 gigameter \(\left( \text{Gm} \right) = 10^9 \: \text{m}\) |
| mega | \(\text{M}\) | 1,000,000 | 1 megameter \(\left( \text{Mm} \right) = 10^6 \: \text{m}\) |
| kilo | \(\text{k}\) | 1,000 | 1 kilometer \(\left( \text{km} \right) = 1,000 \: \text{m}\) |
| 1 | 1 meter \(\left( \text{m} \right)\) | ||
| deci | \(\text{d}\) | 1/10 | 1 decimeter \(\left( \text{dm} \right) = 0.1 \: \text{m}\) |
| centi | \(\text{c}\) | 1/100 | 1 centimeter \(\left( \text{cm} \right) = 0.01 \: \text{m}\) |
| milli | \(\text{m}\) | 1/1,000 | 1 millimeter \(\left( \text{mm} \right) = 0.001 \: \text{m}\) |
| micro | \(\mu\) | 1/1,000,000 | 1 micrometer \(\left( \mu \text{m} \right) = 10^{-6} \: \text{m}\) |
| nano | \(\text{n}\) | 1/1,000,000,000 | 1 nanometer \(\left( \text{nm} \right) = 10^{-9} \: \text{m}\) |
*Micro is often abbreviated "mc" in healthcare to avoid confusion between the \(\mu\) and m which often look similar when written by hand.
There are more prefixes, some of them rarely used, that go far beyond what is given here. Have you ever heard of a zeptometer? You can learn more about prefixes at http://www.bipm.org/en/measurement-units/
Since the metric system is not the usual unit system we use, it can be challenging to understand the relative size of each unit. Go to http://learn.genetics.utah.edu/content/cells/scale and use the slider below the image to zoom in and see how the sizes of objects compare.
There are a couple of odd little practices with the use of unit abbreviations. Most abbreviations are lower-case. We use "\(\text{m}\)" for meter and not "\(\text{M}\)". However, when it comes to volume, the base unit "liter" is abbreviated as "\(\text{L}\)" and not "\(\text{l}\)". So we would write 3.5 milliliters as \(3.5 \: \text{mL}\).
As a practical matter, whenever possible you should express the units in a small and manageable number. If you are measuring the weight of a material that weighs \(6.5 \: \text{kg}\), this is easier than saying it weighs \(6500 \: \text{g}\). Both are correct, bu the \(\text{kg}\) units in this case make for a small and easily managed number.
Temperature Scales
There are three temperature scales that are commonly used in measurement. Their units are \(^\text{o} \text{F}\) (degrees Fahrenheit), \(^\text{o} \text{C}\) (degrees Celsius), and \(\text{K}\) (Kelvin). The Fahrenheit scale, which is the most commonly used scale in the United States, defines the normal freezing point and boiling point of water as \(32^\text{o} \text{F}\) and \(212^\text{o} \text{F}\), respectively. The Celsius scale defines the normal freezing point and boiling point of water as \(0^\text{o} \text{C}\) and \(100^\text{o} \text{C}\), respectively. The Celsius scale is commonly used in most countries across the globe. The Kelvin scale, which is also referred to as the absolute temperature scale, defines absolute zero as the lowest theoretically possible temperature, which means that temperatures expressed in Kelvin cannot be negative numbers.
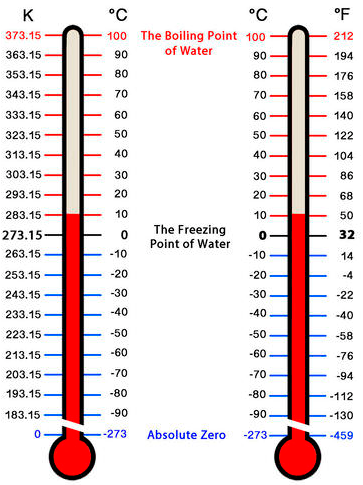
Converting Temperature Scales
Regardless of the temperature scale used, it is important to be able to convert from one scale to another. Here are the conversions we use.
\(^\text{o} \text{F}\) to \(^\text{o} \text{C}\)
\[T_{^\text{o} \text{C}} = \left( T_{^\text{o} \text{F}} - 32 \right) \times \frac{5}{9}\]
\(^\text{o} \text{C}\) to \(^\text{o} \text{F}\)
\[T_{^\text{o} \text{F}} = \frac{9}{5} \times \left( T_{^\text{o} \text{C}} \right) + 32\]
\(^\text{o} \text{C}\) to \(\text{K}\)
\[T_\text{K} = T_{^\text{o} \text{C}} + 273.15\]
\(\text{K}\) to \(^\text{o} \text{C}\)
\[T_{^\text{o} \text{C}} = T_\text{K} - 273.15\]
Example \(\PageIndex{1}\)
The melting point of mercury is \(-38.84^\text{o} \text{C}\). Convert this value to degrees Fahrenheit and Kelvin.
Solution
The formulas above can be used to convert among temperature units. First, the given value can be used to convert from \(^\text{o} \text{C}\) to \(^\text{o} \text{F}\).
\[\begin{align*} T_{^\text{o} \text{F}} &= \frac{9}{5} \times \left( -38.84^\text{o} \text{C} \right) + 32 & \\ T_{^\text{o} \text{F}} &= -37.91^\text{o} \text{F} & \end{align*}\]
Then, the same initial temperature can be used to find the temperature in Kelvin.
\[\begin{align*} T_\text{K} &= -38.84^\text{o} \text{C} + 273.15 & \\ T_\text{K} &= 234.75 \: \text{K} & \end{align*}\]
Supplemental Resources
- Scientific notation practice: http://www.mathisfun.com/numbers/sci...-notation.html
- History of SI Units: http://physics.nist.gov/cuu/Units/history.html
Contributors and Attributions
Allison Soult, Ph.D. (Department of Chemistry, University of Kentucky)

