Aliphatic Nucleophilic Substitution: Rate Laws
In aliphatic nucleophilic substitution, a nucleophile (abbreviated Nu) replaces a halogen "leaving group" (abbreviated LGp) from a tetrahedral carbon. Aliphatic nucleophilic substitution may take place through two different mechanisms:
- C-LGp bond breaking, followed by C-Nu bond formation.
or
- C-Nu bond formation at the same time as C-LGp bond breaking.
A look at the reaction progress diagrams for these two reactions illustrates some big differences. We will look at cyanide anion, a nucleophile, substituting for chloride in 2-chloropropane.
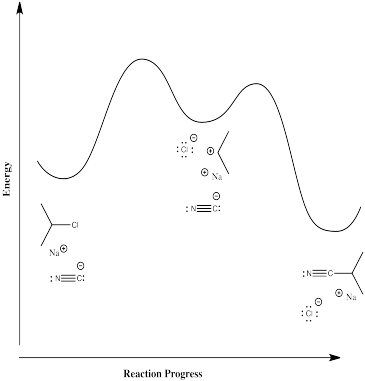
In the first case, some energy must be added in order to break the carbon-chlorine bond. The chlorine forms an anion, leaving a cation on the carbon. This ion pair is an intermediate along the reaction pathway. The cyanide ion then connects with this cation to form the nitrile product. Thus, there are two elementary steps in this mechanism.
Most likely, the first step is the rate-determining step. Breaking bonds costs energy, whereas making bonds releases energy. It is hard to imagine that there could be a significant barrier to the second step; the anion and cation should come together almost automatically.
The rate law for this stepwise mechanism is:
\[ Rate = k[^iPrCl] \]
that is, the rate depends on the first elementary step, but not on the second one. The second step happens pretty much automatically as soon as the first one has finally gotten around to happening.
In the second case, the nucleophile displaces the chloride directly in one step. There is only one elementary step in this reaction, and it requires both compounds to come together at once.
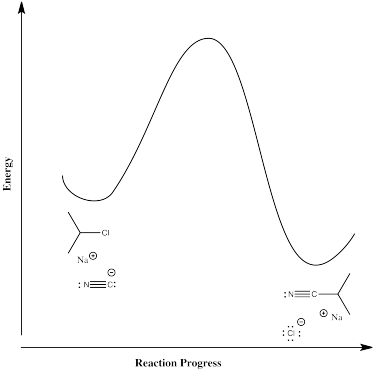
The rate law for this concerted mechanism is:
\[ Rate = k[^iPrCl][^-CN]\]
These two rate laws are very different, and offer an additional way for us to tell how this reaction is taking place. In principle, if we try the reaction with different concentrations of cyanide (but keep the 2-chloropropane concentration constant), we can see whether that has an effect on how quickly the product appears. If it has the predictable effect, maybe the reaction happens in one step. If not, maybe it is a two-step reaction.
Because the rate laws for these two mechanisms are so different, there has arisen a catchy shorthand for describing these reactions based on their rate laws, coined by C.K. Ingold. The rate of the stepwise reaction depends only on one concentration and is referred to as a "unimolecular reaction"; Ingold's shorthand for this kind of nucleophilic substitution was "SN1".
The rate of the concerted reaction depends on two different concentrations and is referred to as a bimolecular reaction; Ingold's shorthand for this reaction was "SN2".
Problem NS3.1.
Suppose you run this reaction with three different concentrations of cyanide: 0.1 mol/L, 0.2 mol/L and 0.3 mol/L. You keep the 2-chloropropane concentration constant at 0.05 mol/L.
- The reaction turns out to be proceeding via a SN1 mechanism. Plot a graph of rate vs.[-CN].
- The reaction turns out to be proceeding via a SN2 mechanism. Plot a graph of rate vs.[-CN].
Now you switch things up and run this reaction with three different concentrations of 2-chloropropane: 0.1 mol/L, 0.2 mol/L and 0.3 mol/L. You keep the 2-chloropropane concentration constant at 0.05 mol/L.
- The reaction turns out to be proceeding via a SN1 mechanism. Plot a graph of rate vs.[iPrCl].
- The reaction turns out to be proceeding via a SN2 mechanism. Plot a graph of rate vs.[iPrCl].
Why would the mechanism proceed in one way and not the other? Molecular choices between pathways like this are often described on the basis of "steric and electronic effects"; in other words, it's either something to do with charge or something to do with crowdedness. We will see soon how these effects can influence the course of the reaction, and how the mechanism can itself have consequences in the formation of different products.
Problem NS3.2.
How might crowdedness or steric effects influence the pathway taken by the reaction between cyanide and 2-chloropropane?
Problem NS3.3.
How might charge stability influence the pathway taken by the reaction between cyanide and 2-chloropropane?




