Optical activity is an effect of an optical isomer's interaction with plane-polarized light.
Introduction
Optical isomers, or enantiomers, have the same sequence of atoms and bonds but are different in their 3D shape. Two enantiomers are nonsuperimposible mirror images of one another (i.e., chiral), with the most common cited example being our hands. Our left hand is a mirror image of our right, yet there is no way our left thumb can be over our right thumb if our palms are facing the same way and placed over one another. Optical isomers also have no axis of symmetry, which means that there is no line that bisects the compound such that the left half is a mirror image of the right half.
Optical isomers have basically the same properties (melting points, boiling points, etc.) but there are a few exceptions (uses in biological mechanisms and optical activity). There are drugs, called enantiopure drugs, that have different effects based on whether the drug is a racemic mixture or purely one enantiomer. For example, d-ethambutol treats tuberculosis, while l-ethambutol causes blindness. Optical activity is the interaction of these enantiomers with plane-polarized light.
A Brief History
Optical activity was first observed by the French physicist Jean-Baptiste Biot. He concluded that the change in direction of plane-polarized light when it passed through certain substances was actually a rotation of light, and that it had a molecular basis. His work was supported by the experimentation of Louis Pasteur. Pasteur observed the existence of two crystals that were mirror images in tartaric acid, an acid found in wine. Through meticulous experimentation, he found that one set of molecules rotated polarized light clockwise while the other rotated light counterclockwise to the same extent. He also observed that a mixture of both, a racemic mixture (or racemic modification), did not rotate light because the optical activity of one molecule canceled the effects of the other molecule. Pasteur was the first to show the existence of chiral molecules.
Rotation of Light
An enantiomer that rotates plane-polarized light in the positive direction, or clockwise, is called dextrorotary [(+), or d-], while the enantiomer that rotates the light in the negative direction, or counterclockwise, is called levorotary [(-), or l-]. When both d- and l- isomers are present in equal amounts, the mixture is called a racemic mixture.

image source
In the picture above, you can see that unpolarized light passes through a filter so that only waves that oscillate in a certain direction can pass through. When these waves interact with an optically active material, they are rotated either clockwise or counterclockwise, depending on the enantiomer. In the case of the image above, the light is rotated clockwise so the substance is the dextrorotary enantiomer.
Measuring Optical Activity
Optical activity is measured by a polarimeter, and is dependent on several factors: concentration of the sample, temperature, length of the sample tube or cell, and wavelength of the light passing through the sample. Rotation is given in +/- degrees, depending on whether the sample has d- (positive) or l- (negative) enantiomers. The standard measurement for rotation for a specific chemical compound is called the specific rotation, defined as an angle measured at a path length of 1 decimeter and a concentration of 1g/ml. The specific rotation of a pure substance is an intrinsic property. In solution, the formula for specific rotation is:
\[ [\alpha]^T_\lambda = \dfrac{\alpha}{I\cdot c}\]
where
- [α] is the specific rotation in degrees cm3 dm-1 g-1.
- λ is the wavelength in nanometers,
- α is the measured angle of rotation of a substance,
- T is the temperature in degrees,
- l is the path length in decimeters,
- c is the concentration in g/ml, and
References
- Pettrucci, Ralph H., Harwood, Herring, Madura. General Chemistry: Principles and Modern Applications. 9th. Upper Saddle River: Pearson Prentice Hall, 2007.
- Raymond, Kenneth W. General Organic and Biological Chemistry. 3rd. Hoboken: John Wiley & Sons, Inc. 2010.
Practice Questions
- Why doesn’t a racemic mixture show optical activity?
- Does the following image show optically active molecules (image source)?

- What would happen if your feet were not optical isomers of each other?
- Your friend has tuberculosis. Assuming you like your friend and you want him to live, which isomer of ethambutol do you give him and why?
- Draw each compound's enantiomer.
Answers
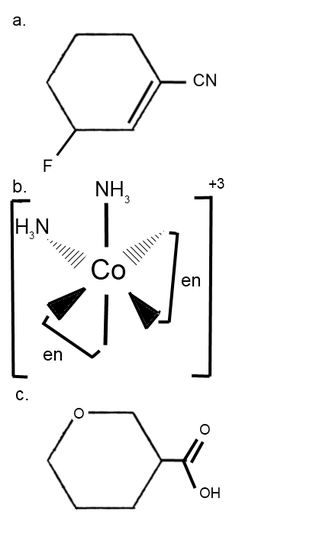
- In a racemic mixture, both dextrorotary and levorotary enantiomers are present in equal amounts, so the overall rotation of polarized light is zero. The clockwise rotation is canceled by the counterclockwise rotation.
- Yes, because the molecules are mirror images of one another.
- You'd be a terrible dancer. (Get it? Two left feet? Haha.)
- Dextrorotary ethambutol, because l-ethambutol would not only fail to cure him, but it would also leave him blind.
- Enantiomers
http://en.Wikipedia.org/wiki/Enantiopure_drug
Contributors
- Nanki J Natt (UCD), Anna Zhu (UCD)




