5.2: Addition of Strong Brønsted Acids
- Page ID
- 205339
Strong Brønsted acids such as HCl, HBr, HI & H2SO4, rapidly add to the C=C functional group of alkenes to give products in which new covalent bonds are formed to hydrogen and to the conjugate base of the acid. Using the above equation as a guide, write the addition products expected on reacting each of these reagents with cyclohexene.
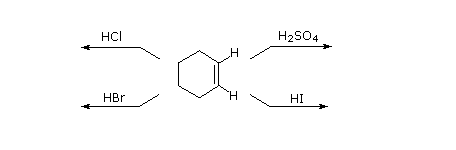
Weak Brønsted acids such as water (pKa = 15.7) and acetic acid (pKa = 4.75) do not normally add to alkenes. However, the addition of a strong acid serves to catalyze the addition of water, and in this way alcohols may be prepared from alkenes. For example, if sulfuric acid is dissolved in water it is completely ionized to the hydronium ion, H3O(+), and this strongly acidic (pKa = -1.74) species effects hydration of ethene and other alkenes.
CH2=CH2 + H3O(+) ——> HCH2–CH2OH + H(+)
The importance of choosing an appropriate solvent for these addition reactions should now be clear. If the addition of HCl, HBr or HI is desired, water and alcohols should not be used. These strong acids will ionize in such solvents to give ROH2(+) and the nucleophilic oxygen of the solvent will compete with the halide anions in the final step, giving alcohol and ether products. By using inert solvents such as hexane, benzene and methylene chloride, these competing solvent additions are avoided. Because these additions proceed by way of polar or ionic intermediates, the rate of reaction is greater in polar solvents, such as nitromethane and acetonitrile, than in non-polar solvents, such as cyclohexane and carbon tetrachloride.
Regioselectivity and the Markovnikov Rule
Only one product is possible from the addition of these strong acids to symmetrical alkenes such as ethene and cyclohexene. However, if the double bond carbon atoms are not structurally equivalent, as in molecules of 1-butene, 2-methyl-2-butene and 1-methylcyclohexene, the reagent conceivably may add in two different ways. This is shown for 2-methyl-2-butene in the following equation.
| (CH3)2C=CHCH3 + H-Cl |  | (CH3)2CH–CHClCH3 | or | (CH3)2CCl–CHHCH3 |
| 2-methyl-2-butene | 2-chloro-3-methylbutane | 2-chloro-2-methylbutane |
When addition reactions to such unsymmetrical alkenes are carried out, we find that one of the two possible constitutionally isomeric products is formed preferentially. Selectivity of this sort is termed regioselectivity. In the above example, 2-chloro-2-methylbutane is nearly the exclusive product. Similarly, 1-butene forms 2-bromobutane as the predominant product on treatment with HBr.
After studying many addition reactions of this kind, the Russian chemist Vladimir Markovnikov noticed a trend in the structure of the favored addition product. He formulated this trend as an empirical rule we now call The Markovnikov Rule: When a Brønsted acid, HX, adds to an unsymmetrically substituted double bond, the acidic hydrogen of the acid bonds to that carbon of the double bond that has the greater number of hydrogen atoms already attached to it.
In more homelier vernacular this rule may be restated as, "Them that has gits."
It is a helpful exercise to predict the favored product in examples such as those shown below:
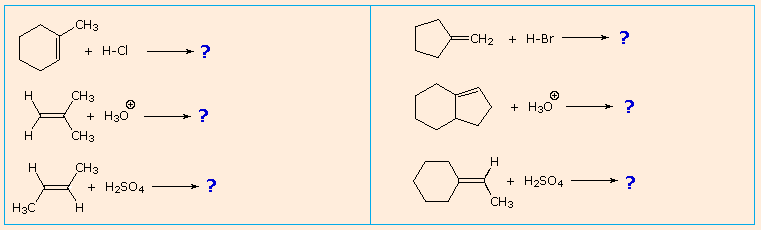
Empirical rules like the Markovnikov Rule are useful aids for remembering and predicting experimental results. Indeed, empirical rules are often the first step toward practical mastery of a subject, but they seldom constitute true understanding. The Markovnikov Rule, for example, suggests there are common and important principles at work in these addition reactions, but it does not tell us what they are. The next step in achieving an understanding of this reaction must be to construct a rational mechanistic model that can be tested by experiment.
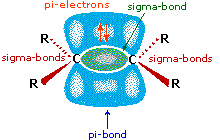
All the reagents discussed here are strong Brønsted acids so, as a first step, it seems sensible to find a base with which the acid can react. Since we know that these acids do not react with alkanes, it must be the pi-electrons of the alkene double bond that serve as the base. As shown in the diagram on the right, the pi-orbital extends into the space immediately above and below the plane of the double bond, and the electrons occupying this orbital may be attracted to the proton of a Brønsted acid. The resulting acid-base equilibrium generates a carbocation intermediate (the conjugate acid of the alkene) which then combines rapidly with the anionic conjugate base of the Brønsted acid. This two-step mechanism is illustrated for the reaction of ethene with hydrogen chloride by the following equations.
| First Step: H2C=CH2 + HCl |  | HH2C–CH2(+) + Cl(–) | |
| Second Step: HH2C–CH2(+) + Cl(–) |  | HH2C–CH2Cl |
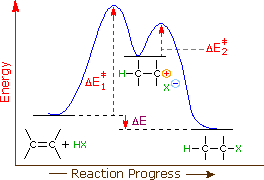
An energy diagram for this two-step addition mechanism is shown to the left. From this diagram we see that the slow or rate-determining step (the first step) is also the product determining step (the anion will necessarily bond to the carbocation site). Electron donating double bond substituents increase the reactivity of an alkene, as evidenced by the increased rate of hydration of 2-methylpropene (two alkyl groups) compared with 1-butene (one alkyl group). Evidently, alkyl substituents act to increase the rate of addition by lowering the activation energy, ΔE‡1 of the rate determining step, and it is here we should look for a rationalization of Markovnikov's rule.
As expected, electron withdrawing substituents, such as fluorine or chlorine, reduce the reactivity of an alkene to addition by acids (vinyl chloride is less reactive than ethene).
George Hammond formulated a useful principle that relates the nature of a transition state to its location on the reaction path. This Hammond Postulate states that a transition state will be structurally and energetically similar to the species (reactant, intermediate or product) nearest to it on the reaction path. In strongly exothermic reactions the transition state will resemble the reactant species. In strongly endothermic conversions, such as that shown to the right, the transition state will resemble the high-energy intermediate or product, and will track the energy of this intermediate if it changes. This change in transition state energy and activation energy as the stability of the intermediate changes may be observed by clicking the higher or lower buttons to the right of the energy diagram. Three examples may be examined, and the reference curve is changed to gray in the diagrams for higher (magenta) and lower (green) energy intermediates.
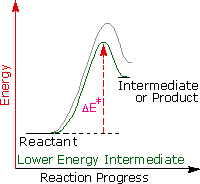

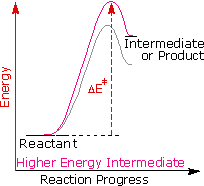
The carbocation intermediate formed in the first step of the addition reaction now assumes a key role, in that it directly influences the activation energy for this step. Independent research shows that the stability of carbocations varies with the nature of substituents, in a manner similar to that seen for alkyl radicals. The exceptional stability of allyl and benzyl cations is the result of charge delocalization, and the stabilizing influence of alkyl substituents, although less pronounced, has been interpreted in a similar fashion.
|
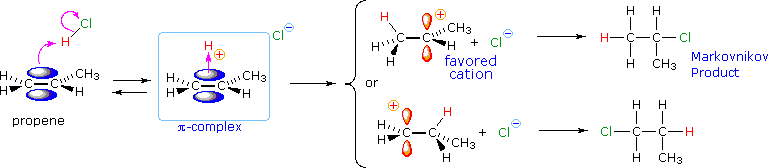
From this information, applying the Hammond Postulate, we arrive at a plausible rationalization of Markovnikov's rule. When an unsymmetrically substituted double bond is protonated, we expect the more stable carbocation intermediate to be formed faster than the less stable alternative, because the activation energy of the path to the former is the lower of the two possibilities. This is illustrated by the following equation for the addition of hydrogen chloride to propene. Note that the initial acid-base equilibrium leads to a pi-complex which immediately reorganizes to a sigma-bonded carbocation intermediate. The more stable 2º-carbocation is formed preferentially, and the conjugate base of the Brønsted acid (chloride anion in the example shown below) then rapidly bonds to this electrophilic intermediate to form the final product.
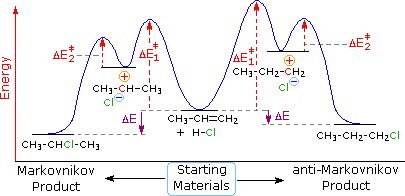
The following energy diagram summarizes these features. Note that the pi-complex is not shown, since this rapidly and reversibly formed species is common to both possible reaction paths.
A more extensive discussion of the factors that influence carbocation stability may be accessed by Clicking Here.
Contributors
- William Reusch, Professor Emeritus (Michigan State U.), Virtual Textbook of Organic Chemistry



