Going back to the expression for changes in internal energy that stems from assuming that \(U\) is a function of \(V\) and \(T\) (or \(U(V, T)\) for short)
\[ dU = \left( \dfrac{\partial U}{\partial V} \right)_TdV+ \left( \dfrac{\partial U}{\partial T} \right)_V dT \nonumber \]
one quickly recognizes one of the terms as the constant volume heat capacity, \(C_V\). And so the expression can be re-written
\[ dU = \left( \dfrac{\partial U}{\partial V} \right)_T dV + C_V dT \nonumber \]
But what about the first term? The partial derivative is a coefficient called the “internal pressure”, and given the symbol \(\pi_T\).
\[ \pi_T = \left( \dfrac{\partial U}{\partial V} \right)_T \nonumber \]
James Prescott Joule (1818-1889) recognized that \(\pi_T\) should have units of pressure (Energy/volume = pressure) and designed an experiment to measure it.
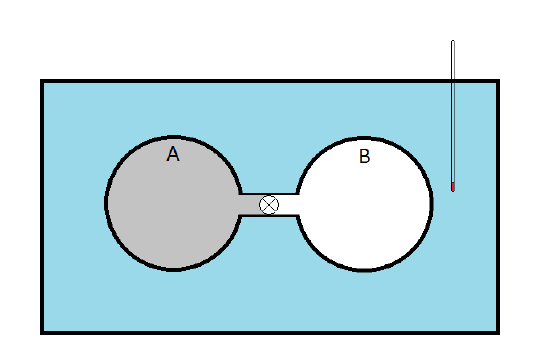
He immersed two copper spheres, A and B, connected by a stopcock. Sphere A is filled with a sample of gas while sphere B was evacuated. The idea was that when the stopcock was opened, the gas in sphere A would expand (\(\Delta V > 0\)) against the vacuum in sphere B (doing no work since \(p_{ext} = 0\). The change in the internal energy could be expressed
\[ dU = \pi_T dV + C_V dT \nonumber \]
But also, from the first law of thermodynamics
\[ dU = dq + dw \nonumber \]
Equating the two
\[ \pi_T dV + C_V dT = dq + dw \nonumber \]
and since \(dw = 0\)
\[ \pi_T dV + C_V dT = dq \nonumber \]
Joule concluded that \(dq = 0\) (and \(dT = 0\) as well) since he did not observe a temperature change in the water bath which could only have been caused by the metal spheres either absorbing or emitting heat. And because \(dV > 0\) for the gas that underwent the expansion into an open space, \(\pi_T\) must also be zero! In truth, the gas did undergo a temperature change, but it was too small to be detected within his experimental precision. Later, we (once we develop the Maxwell Relations) will show that
\[ \left( \dfrac{\partial U}{\partial V} \right)_T = T \left( \dfrac{\partial p}{\partial T} \right)_V -p \label{eq3} \]
Application to an Ideal Gas
For an ideal gas \(p = RT/V\), so it is easy to show that
\[\left( \dfrac{\partial p}{\partial T} \right)_V = \dfrac{R}{V} \label{eq4} \]
so combining Equations \ref{eq3} and \ref{eq4} together to get
\[ \left( \dfrac{\partial U}{\partial V} \right)_T = \dfrac{RT}{V} - p \label{eq5} \]
And since also becuase \(p = RT/V\), then Equation \ref{eq5} simplifies to
\[ \left( \dfrac{\partial U}{\partial V} \right)_T = p -p = 0 \nonumber \]
So while Joule’s observation was consistent with limiting ideal behavior, his result was really an artifact of his experimental uncertainty masking what actually happened.
Appliation to a van der Waals Gas
For a van der Waals gas,
\[ p = \dfrac{RT}{V-b} - \dfrac{a}{V^2} \label{eqV1} \]
so
\[\left( \dfrac{\partial p}{\partial T} \right)_V = \dfrac{R}{V-b} \label{eqV2} \]
and
\[ \left( \dfrac{\partial U}{\partial V} \right)_T = T\dfrac{R}{V-b} - p \label{eqV3} \]
Substitution of the expression for \(p\) (Equation \ref{eqV1}) into this Equation \ref{eqV3}
\[ \left( \dfrac{\partial U}{\partial V} \right)_T = \dfrac{a}{V^2} \nonumber \]
In general, it can be shown that
\[\left( \dfrac{\partial p}{\partial T} \right)_V = \dfrac{\alpha}{\kappa_T} \nonumber \]
And so the internal pressure can be expressed entirely in terms of measurable properties
\[ \left( \dfrac{\partial U}{\partial V} \right)_T = T \dfrac{\alpha}{\kappa_T}-p \nonumber \]
and need not apply to only gases (real or ideal)!



