13.2.3: Phase Equilibrium in Solutions - Nonvolatile Solutes
- Last updated
- Save as PDF
- Page ID
- 339048
Learning Objectives
- To describe the relationship between solute concentration and the physical properties of a solution.
- To understand that the total number of nonvolatile solute particles determines the decrease in vapor pressure, increase in boiling point, and decrease in freezing point of a solution versus the pure solvent.
Many of the physical properties of solutions differ significantly from those of the pure substances discussed in earlier chapters, and these differences have important consequences. For example, the limited temperature range of liquid water (0°C–100°C) severely limits its use. Aqueous solutions have both a lower freezing point and a higher boiling point than pure water. Probably one of the most familiar applications of this phenomenon is the addition of ethylene glycol (“antifreeze”) to the water in an automobile radiator. This solute lowers the freezing point of the water, preventing the engine from cracking in very cold weather from the expansion of pure water on freezing. Antifreeze also enables the cooling system to operate at temperatures greater than 100°C without generating enough pressure to explode.
Changes in the freezing point and boiling point of a solution depend primarily on the number of solute particles present rather than the kind of particles. Such properties of solutions are called colligative properties (from the Latin colligatus, meaning “bound together” as in a quantity). As we will see, the vapor pressure and osmotic pressure of solutions are also colligative properties.
Counting Concentrations and Effective Concentrations
When we determine the number of particles in a solution, it is important to remember that not all solutions with the same molarity contain the same concentration of solute particles. Consider, for example, 0.01 M aqueous solutions of sucrose, \(\ce{NaCl}\), and \(\ce{CaCl_2}\). Because sucrose dissolves to give a solution of neutral molecules, the concentration of solute particles in a 0.01 M sucrose solution is 0.01 M. In contrast, both \(\ce{NaCl}\) and \(\ce{CaCl_2}\) are ionic compounds that dissociate in water to yield solvated ions. As a result, a 0.01 M aqueous solution of \(\ce{NaCl}\) contains 0.01 M \(\ce{Na^{+}}\) ions and 0.01 M \(\ce{Cl^{−}}\) ions, for a total particle concentration of 0.02 M. Similarly, the \(\ce{CaCl_2}\) solution contains 0.01 M \(\ce{Ca^{2+}}\) ions and 0.02 M \(\ce{Cl^{−}}\) ions, for a total particle concentration of 0.03 M. These values are correct for dilute solutions, where the dissociation of the compounds to form separately solvated ions is complete.
At higher concentrations (typically >1 M), especially with salts of small, highly charged ions (such as \(\ce{Mg^{2+}}\) or \(\ce{Al^{3+}}\)), or in solutions with less polar solvents, dissociation to give separate ions is often incomplete. The sum of the concentrations of the dissolved solute particles dictates the physical properties of a solution. In the following discussion, we must therefore keep the chemical nature of the solute firmly in mind. A greater discussion of this is below.
Vapor Pressure of Solutions and Raoult’s Law For Nonvolatile Solutes
Adding a nonvolatile solute, one whose vapor pressure is too low to measure readily, to a volatile solvent decreases the vapor pressure of the solvent. We can understand this phenomenon qualitatively by examining Figure \(\PageIndex{1}\), which is a schematic diagram of the surface of a solution of glucose in water. In an aqueous solution of glucose, a portion of the surface area is occupied by nonvolatile glucose molecules rather than by volatile water molecules. As a result, fewer water molecules can enter the vapor phase per unit time, even though the surface water molecules have the same kinetic energy distribution as they would in pure water. At the same time, the rate at which water molecules in the vapor phase collide with the surface and reenter the solution is unaffected. The net effect is to shift the dynamic equilibrium between water in the vapor and the liquid phases, decreasing the vapor pressure of the solution compared with the vapor pressure of the pure solvent.
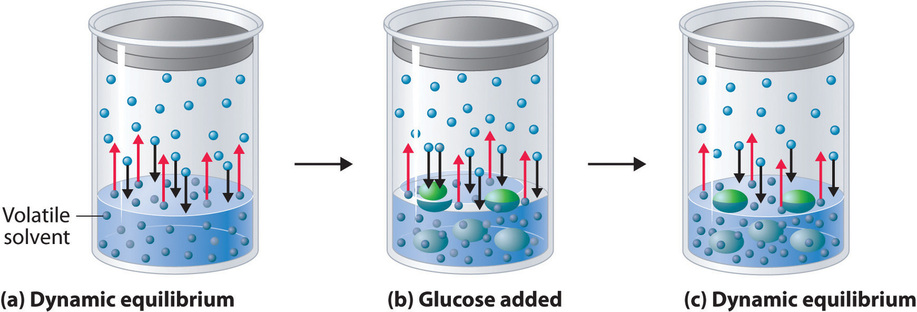
Figure \(\PageIndex{2}\) shows two beakers, one containing pure water and one containing an aqueous glucose solution, in a sealed chamber. We can view the system as having two competing equilibria: water vapor will condense in both beakers at the same rate, but water molecules will evaporate more slowly from the glucose solution because fewer water molecules are at the surface. Eventually all of the water will evaporate from the beaker containing the liquid with the higher vapor pressure (pure water) and condense in the beaker containing the liquid with the lower vapor pressure (the glucose solution). If the system consisted of only a beaker of water inside a sealed container, equilibrium between the liquid and vapor would be achieved rather rapidly, and the amount of liquid water in the beaker would remain constant.
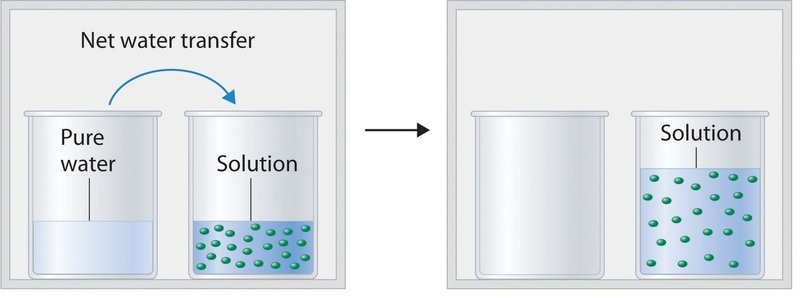
If the particles of a solute are essentially the same size as those of the solvent and both solute and solvent have roughly equal probabilities of being at the surface of the solution, then the effect of a solute on the vapor pressure of the solvent is proportional to the number of sites occupied by solute particles at the surface of the solution. Doubling the concentration of a given solute causes twice as many surface sites to be occupied by solute molecules, resulting in twice the decrease in vapor pressure. The relationship between solution composition and vapor pressure is therefore
\[P_A=\chi_AP^0_A \label{13.5.1}\]
where \(P_A\) is the vapor pressure of component A of the solution (in this case the solvent), \(\chi_A\) is the mole fraction of \(A\) in solution, and \(P^0_A\) is the vapor pressure of pure \(A\). Equation \(\ref{13.5.1}\) is known as Raoult’s law, after the French chemist who developed it. If the solution contains only a single nonvolatile solute (\(B\)), then we can relate the mole fraction of the solvent to the solute
\[\chi_A + \chi_B = 1 \nonumber\]
and we can substitute \(\chi_A = 1 − \chi_B\) into Equation \ref{13.5.1} to obtain
\[\begin{align*} P_A &=(1−\chi_B)P^0_A \\[4pt] &=P^0_A−\chi_BP^0_A \end{align*}\]
Rearranging and defining \(ΔP_A=P^0_A−P_A\), we obtain a relationship between the decrease in vapor pressure and the mole fraction of nonvolatile solute:
\[ \begin{align} P^0_A−P_A &=ΔP_A \\[4pt] &=\chi_BP^0_A \label{13.5.3} \end{align}\]
We can solve vapor pressure problems in either of two ways: by using Equation \(\ref{13.5.1}\) to calculate the actual vapor pressure above a solution of a nonvolatile solute, or by using Equation \(\ref{13.5.3}\) to calculate the decrease in vapor pressure caused by a specified amount of a nonvolatile solute.
Example \(\PageIndex{1}\): Anti-Freeze
Ethylene glycol (\(\ce{HOCH_2CH_2OH}\)), the major ingredient in commercial automotive antifreeze, increases the boiling point of radiator fluid by lowering its vapor pressure. At 100°C, the vapor pressure of pure water is 760 mmHg. Calculate the vapor pressure of an aqueous solution containing 30.2% ethylene glycol by mass, a concentration commonly used in climates that do not get extremely cold in winter.
Given: identity of solute, percentage by mass, and vapor pressure of pure solvent
Asked for: vapor pressure of solution
Strategy:
- Calculate the number of moles of ethylene glycol in an arbitrary quantity of water, and then calculate the mole fraction of water.
- Use Raoult’s law (Equation \ref{13.5.1}) to calculate the vapor pressure of the solution.
Solution:
A A 30.2% solution of ethylene glycol contains 302 g of ethylene glycol per kilogram of solution; the remainder (698 g) is water. To use Raoult’s law to calculate the vapor pressure of the solution, we must know the mole fraction of water. Thus we must first calculate the number of moles of both ethylene glycol (EG) and water present:
\[moles \; EG=(302 \;\cancel{g}) \left( \dfrac{1\; mol}{62.07\; \cancel{g}} \right)=4.87\; mol\; EG \nonumber\]
\[moles \; \ce{H2O} =(698 \;\cancel{g}) \left( \dfrac{1\; mol}{18.02\; \cancel{g}} \right)=38.7\; mol\; H_2O \nonumber\]
The mole fraction of water is thus
\[\chi_{H_2O}=\dfrac{38.7\; \cancel{mol} \; H_2O}{38.7\; \cancel{mol}\; H_2O +4.87 \cancel{mol}\; EG} =0.888 \nonumber\]
B From Raoult’s law (Equation \(\ref{13.5.1}\)), the vapor pressure of the solution is
\[ \begin{align*} P_{\ce{H2O}} &=(\chi_{\ce{H2O}})(P^0_{\ce{H2O}}) \\[4pt] &=(0.888)(760\; mmHg) =675 \;mmHg \end{align*}\]
Alternatively, we could solve this problem by calculating the mole fraction of ethylene glycol and then using Equation \(\ref{13.5.3}\) to calculate the resulting decrease in vapor pressure:
\[\begin{align*} \chi_{EG} &=\dfrac{4.87\; mol\; EG}{4.87\; mol\; EG+38.7\; mol\; H_2O} \\[4pt] &=0.112 \end{align*}\]
\[\begin{align*} ΔP_{\ce{H2O}} &=(\chi_{EG})(P^0_{\ce{H2O}}) \\[4pt] &=(0.112)(760\; mmHg)=85.1\; mmHg \end{align*}\]
\[P_{\ce{H2O}}=P^0_{\ce{H2O}}−ΔP_{\ce{H2O}}=760\; mmHg−85.1\; mmHg=675\; mmHg \nonumber\]
The same result is obtained using either method.
Exercise \(\PageIndex{1}\)
Seawater is an approximately 3.0% aqueous solution of \(\ce{NaCl}\) by mass with about 0.5% of other salts by mass. Calculate the decrease in the vapor pressure of water at 25°C caused by this concentration of \(\ce{NaCl}\), remembering that 1 mol of \(\ce{NaCl}\) produces 2 mol of solute particles. The vapor pressure of pure water at 25°C is 23.8 mmHg.
- Answer
-
0.45 mmHg. This may seem like a small amount, but it constitutes about a 2% decrease in the vapor pressure of water and accounts in part for the higher humidity in the north-central United States near the Great Lakes, which are freshwater lakes. The decrease therefore has important implications for climate modeling.
Boiling Point Elevation
Recall that the normal boiling point of a substance is the temperature at which the vapor pressure equals 1 atm. If a nonvolatile solute lowers the vapor pressure of a solvent, it must also affect the boiling point. Because the vapor pressure of the solution at a given temperature is less than the vapor pressure of the pure solvent, achieving a vapor pressure of 1 atm for the solution requires a higher temperature than the normal boiling point of the solvent. Thus the boiling point of a solution is always greater than that of the pure solvent. We can see why this must be true by comparing the phase diagram for an aqueous solution with the phase diagram for pure water (Figure \(\PageIndex{4}\)). The vapor pressure of the solution is less than that of pure water at all temperatures. Consequently, the liquid–vapor curve for the solution crosses the horizontal line corresponding to \(P = 1\, atm\) at a higher temperature than does the curve for pure water.
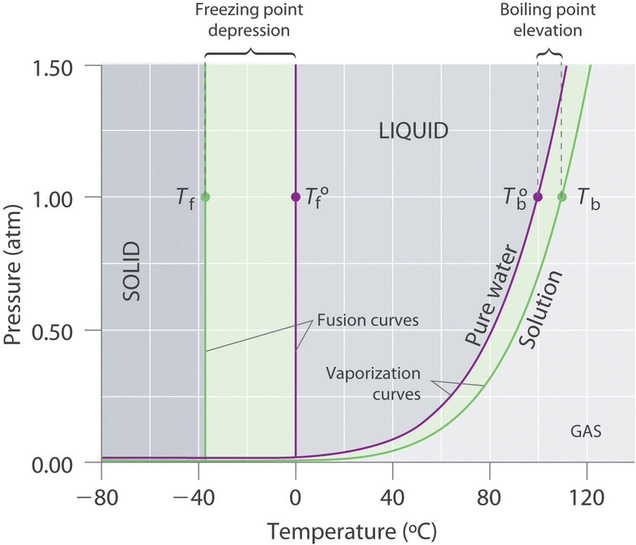
The boiling point of a solution with a nonvolatile solute is always greater than the boiling point of the pure solvent.
The magnitude of the increase in the boiling point is related to the magnitude of the decrease in the vapor pressure. As we have just discussed, the decrease in the vapor pressure is proportional to the concentration of the solute in the solution. Hence the magnitude of the increase in the boiling point must also be proportional to the concentration of the solute (Figure \(\PageIndex{5}\)).
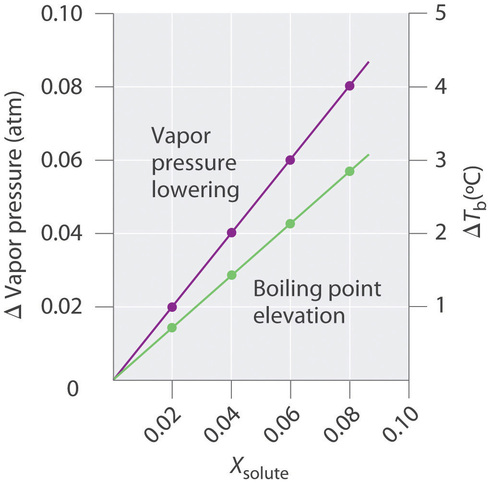
We can define the boiling point elevation (\(ΔT_b\)) as the difference between the boiling points of the solution and the pure solvent:
\[ΔT_b=T_b−T^0_b \label{13.5.8}\]
where \(T_b\) is the boiling point of the solution and \(T^0_b\) is the boiling point of the pure solvent. We can express the relationship between \(ΔT_b\) and concentration as follows
\[ΔT_b = mK_b \label{13.5.9}\]
where m is the concentration of the solute expressed in molality, and \(K_b\) is the molal boiling point elevation constant of the solvent, which has units of °C/m. Table \(\PageIndex{1}\) lists characteristic \(K_b\) values for several commonly used solvents. For relatively dilute solutions, the magnitude of both properties is proportional to the solute concentration.
| Solvent | Boiling Point (°C) | Kb (°C/m) | Freezing Point (°C) | Kf (°C/m) |
|---|---|---|---|---|
| acetic acid | 117.90 | 3.22 | 16.64 | 3.63 |
| benzene | 80.09 | 2.64 | 5.49 | 5.07 |
| d-(+)-camphor | 207.4 | 4.91 | 178.8 | 37.8 |
| carbon disulfide | 46.2 | 2.42 | −112.1 | 3.74 |
| carbon tetrachloride | 76.8 | 5.26 | −22.62 | 31.4 |
| chloroform | 61.17 | 3.80 | −63.41 | 4.60 |
| nitrobenzene | 210.8 | 5.24 | 5.70 | 6.87 |
| water | 100.00 | 0.51 | 0.00 | 1.86 |
The concentration of the solute is typically expressed as molality rather than mole fraction or molarity for two reasons. First, because the density of a solution changes with temperature, the value of molarity also varies with temperature. If the boiling point depends on the solute concentration, then by definition the system is not maintained at a constant temperature. Second, molality and mole fraction are proportional for relatively dilute solutions, but molality has a larger numerical value (a mole fraction can be only between zero and one). Using molality allows us to eliminate nonsignificant zeros.
According to Table \(\PageIndex{1}\), the molal boiling point elevation constant for water is 0.51°C/m. Thus a 1.00 m aqueous solution of a nonvolatile molecular solute such as glucose or sucrose will have an increase in boiling point of 0.51°C, to give a boiling point of 100.51°C at 1.00 atm. The increase in the boiling point of a 1.00 m aqueous \(\ce{NaCl}\) solution will be approximately twice as large as that of the glucose or sucrose solution because 1 mol of \(\ce{NaCl}\) produces 2 mol of dissolved ions. Hence a 1.00 m \(\ce{NaCl}\) solution will have a boiling point of about 101.02°C.
Example \(\PageIndex{3}\)
In Example \(\PageIndex{1}\), we calculated that the vapor pressure of a 30.2% aqueous solution of ethylene glycol at 100°C is 85.1 mmHg less than the vapor pressure of pure water. We stated (without offering proof) that this should result in a higher boiling point for the solution compared with pure water. Now that we have seen why this assertion is correct, calculate the boiling point of the aqueous ethylene glycol solution.
Given: composition of solution
Asked for: boiling point
Strategy:
Calculate the molality of ethylene glycol in the 30.2% solution. Then use Equation \(\ref{13.5.9}\) to calculate the increase in boiling point.
Solution:
From Example \(\PageIndex{1}\), we know that a 30.2% solution of ethylene glycol in water contains 302 g of ethylene glycol (4.87 mol) per 698 g of water. The molality of the solution is thus
\[\begin{align*} \text{molality of ethylene glycol} &= \left(\dfrac{4.87 \;mol}{698 \; \cancel{g} \;H_2O} \right) \left(\dfrac{1000\; \cancel{g}}{1 \;kg} \right) \\[4pt] &=6.98\, m \end{align*}\]
From Equation \(\ref{13.5.9}\), the increase in boiling point is therefore
\[\begin{align*} ΔT_b &= m K_b \\[4pt] &=(6.98 \cancel{m})(0.51°C/\cancel{m}) \\[4pt] &=3.6°C \end{align*}\]
The boiling point of the solution is thus predicted to be 104°C. With a solute concentration of almost 7 m, however, the assumption of a dilute solution used to obtain Equation \(\ref{13.5.9}\) may not be valid.
Exercise \(\PageIndex{3}\)
Assume that a tablespoon (5.00 g) of \(\ce{NaCl}\) is added to 2.00 L of water at 20.0°C, which is then brought to a boil to cook spaghetti. At what temperature will the water boil?
- Answer
-
100.04°C, or 100°C to three significant figures. (Recall that 1 mol of \(\ce{NaCl}\) produces 2 mol of dissolved particles. The small increase in temperature means that adding salt to the water used to cook pasta has essentially no effect on the cooking time.)
Freezing Point Depression
The phase diagram in Figure \(\PageIndex{4}\) shows that dissolving a nonvolatile solute in water not only raises the boiling point of the water but also lowers its freezing point. The solid–liquid curve for the solution crosses the line corresponding to \(P = 1\,atm\) at a lower temperature than the curve for pure water.
We can understand this result by imagining that we have a sample of water at the normal freezing point temperature, where there is a dynamic equilibrium between solid and liquid. Water molecules are continuously colliding with the ice surface and entering the solid phase at the same rate that water molecules are leaving the surface of the ice and entering the liquid phase. If we dissolve a nonvolatile solute such as glucose in the liquid, the dissolved glucose molecules will reduce the number of collisions per unit time between water molecules and the ice surface because some of the molecules colliding with the ice will be glucose. Glucose, though, has a very different structure than water, and it cannot fit into the ice lattice. Consequently, the presence of glucose molecules in the solution can only decrease the rate at which water molecules in the liquid collide with the ice surface and solidify. Meanwhile, the rate at which the water molecules leave the surface of the ice and enter the liquid phase is unchanged. The net effect is to cause the ice to melt. The only way to reestablish a dynamic equilibrium between solid and liquid water is to lower the temperature of the system, which decreases the rate at which water molecules leave the surface of the ice crystals until it equals the rate at which water molecules in the solution collide with the ice.
By analogy to our treatment of boiling point elevation,the freezing point depression (\(ΔT_f\)) is defined as the difference between the freezing point of the pure solvent and the freezing point of the solution:
\[ ΔT_f=T^0_f−T_f \label{13.5.10}\]
where \(T^0_f\) is the freezing point of the pure solvent and \(T_f\) is the freezing point of the solution.
The order of the terms is reversed compared with Equation \(\ref{13.5.8}\) to express the freezing point depression as a positive number. The relationship between \(ΔT_f\) and the solute concentration is given by an equation analogous to Equation \(\ref{13.5.9}\):
\[ΔT_f = mK_f \label{13.5.11}\]
where \(m\) is the molality of the solution and \(K_f\) is the molal freezing point depression constant for the solvent (in units of °C/m).
Like \(K_b\), each solvent has a characteristic value of \(K_f\) (see Table \(\PageIndex{1}\)). Freezing point depression depends on the total number of dissolved nonvolatile solute particles, just as with boiling point elevation. Thus an aqueous \(\ce{NaCl}\) solution has twice as large a freezing point depression as a glucose solution of the same molality.
People who live in cold climates use freezing point depression to their advantage in many ways. For example, salt is used to melt ice and snow on roads and sidewalks, ethylene glycol is added to engine coolant water to prevent an automobile engine from being destroyed, and methanol is added to windshield washer fluid to prevent the fluid from freezing.
The decrease in vapor pressure, increase in boiling point, and decrease in freezing point of a solution versus a pure liquid all depend on the total number of dissolved nonvolatile solute particles.
Example \(\PageIndex{4}\): Salting the Roads
In colder regions of the United States, \(\ce{NaCl}\) or \(\ce{CaCl_2}\) is often sprinkled on icy roads in winter to melt the ice and make driving safer. Use the data in the Figure below to estimate the concentrations of two saturated solutions at 0°C, one of \(\ce{NaCl}\) and one of \(\ce{CaCl_2}\), and calculate the freezing points of both solutions to see which salt is likely to be more effective at melting ice.
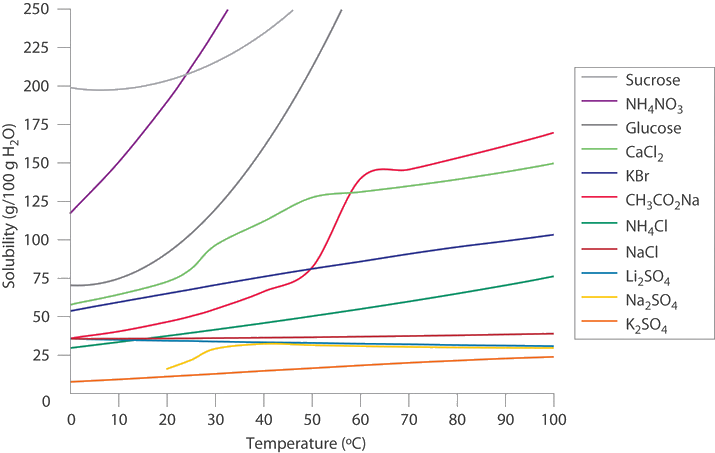
Given: solubilities of two compounds
Asked for: concentrations and freezing points
Strategy:
- Estimate the solubility of each salt in 100 g of water from the figure. Determine the number of moles of each in 100 g and calculate the molalities.
- Determine the concentrations of the dissolved salts in the solutions. Substitute these values into Equation \(\ref{13.5.11}\) to calculate the freezing point depressions of the solutions.
Solution:
A. From Figure above, we can estimate the solubilities of \(\ce{NaCl}\) and \(\ce{CaCl_2}\) to be about 36 g and 60 g, respectively, per 100 g of water at 0°C. The corresponding concentrations in molality are
\[m_{NaCl}=\left(\dfrac{36 \; \cancel{g \;NaCl}}{100 \;\cancel{g} \;H_2O}\right)\left(\dfrac{1\; mol\; NaCl}{58.44\; \cancel{ g\; NaCl}}\right)\left(\dfrac{1000\; \cancel{g}}{1\; kg}\right)=6.2\; m \nonumber\]
\[m_{CaCl_2}=\left(\dfrac{60\; \cancel{g\; CaCl_2}}{100\;\cancel{g}\; H_2O}\right)\left(\dfrac{1\; mol\; CaCl_2}{110.98\; \cancel{g\; CaCl_2}}\right)\left(\dfrac{1000 \;\cancel{g}}{1 kg}\right)=5.4\; m \nonumber \]
The lower formula mass of \(\ce{NaCl}\) more than compensates for its lower solubility, resulting in a saturated solution that has a slightly higher concentration than \(\ce{CaCl2}\).
B. Because these salts are ionic compounds that dissociate in water to yield two and three ions per formula unit of \(\ce{NaCl}\) and \(\ce{CaCl2}\), respectively, the actual concentrations of the dissolved species in the two saturated solutions are 2 × 6.2 m = 12 m for \(\ce{NaCl}\) and 3 × 5.4 m = 16 m for \(\ce{CaCl2}\). The resulting freezing point depressions can be calculated using Equation \(\ref{13.5.11}\):
\[\ce{NaCl}: ΔT_f=mK_f=(12\; \cancel{m})(1.86°C/\cancel{m})=22°C \nonumber\]
\[\ce{CaCl2}: ΔT_f=mK_f=(16\;\cancel{m})(1.86°C/\cancel{m})=30°C \nonumber\]
Because the freezing point of pure water is 0°C, the actual freezing points of the solutions are −22°C and −30°C, respectively. Note that \(\ce{CaCl2}\) is substantially more effective at lowering the freezing point of water because its solutions contain three ions per formula unit. In fact, \(\ce{CaCl2}\) is the salt usually sold for home use, and it is also often used on highways.
Because the solubilities of both salts decrease with decreasing temperature, the freezing point can be depressed by only a certain amount, regardless of how much salt is spread on an icy road. If the temperature is significantly below the minimum temperature at which one of these salts will cause ice to melt (say −35°C), there is no point in using salt until it gets warmer
Exercise \(\PageIndex{4}\)
Calculate the freezing point of the 30.2% solution of ethylene glycol in water whose vapor pressure and boiling point we calculated in Examples \(\PageIndex{1}\) and \(\PageIndex{3}\).
- Answer
-
−13.0°C
Example \(\PageIndex{5}\)
Arrange these aqueous solutions in order of decreasing freezing points: 0.1 m \(\ce{KCl}\), 0.1 m glucose, 0.1 m \(\ce{SrCl2}\), 0.1 m ethylene glycol, 0.1 m benzoic acid, and 0.1 m \(\ce{HCl}\).
Given: molalities of six solutions
Asked for: relative freezing points
Strategy:
- Identify each solute as a strong, weak, or nonelectrolyte, and use this information to determine the number of solute particles produced.
- Multiply this number by the concentration of the solution to obtain the effective concentration of solute particles. The solution with the highest effective concentration of solute particles has the largest freezing point depression.
Solution:
A Because the molal concentrations of all six solutions are the same, we must focus on which of the substances are strong electrolytes, which are weak electrolytes, and which are nonelectrolytes to determine the actual numbers of particles in solution. \(\ce{KCl}\), \(\ce{SrCl_2}\), and \(\ce{HCl}\) are strong electrolytes, producing two, three, and two ions per formula unit, respectively. Benzoic acid is a weak electrolyte (approximately one particle per molecule), and glucose and ethylene glycol are both nonelectrolytes (one particle per molecule).
B The molalities of the solutions in terms of the total particles of solute are: \(\ce{KCl}\) and \(\ce{HCl}\), 0.2 m; \(SrCl_2\), 0.3 m; glucose and ethylene glycol, 0.1 m; and benzoic acid, 0.1–0.2 m. Because the magnitude of the decrease in freezing point is proportional to the concentration of dissolved particles, the order of freezing points of the solutions is: glucose and ethylene glycol (highest freezing point, smallest freezing point depression) > benzoic acid > \(\ce{HCl}\) = \(\ce{KCl}\) > \(\ce{SrCl_2}\).
Exercise \(\PageIndex{5}\)
Arrange these aqueous solutions in order of increasing freezing points: 0.2 m \(\ce{NaCl}\), 0.3 m acetic acid, 0.1 m \(\ce{CaCl_2}\), and 0.2 m sucrose.
- Answer
-
0.2 m \(\ce{NaCl}\) (lowest freezing point) < 0.3 m acetic acid ≈ 0.1 m \(\ce{CaCl_2}\) < 0.2 m sucrose (highest freezing point)
Colligative properties can also be used to determine the molar mass of an unknown compound. One method that can be carried out in the laboratory with minimal equipment is to measure the freezing point of a solution with a known mass of solute. This method is accurate for dilute solutions (≤1% by mass) because changes in the freezing point are usually large enough to measure accurately and precisely. By comparing \(K_b\) and \(K_f\) values in Table \(\PageIndex{1}\), we see that changes in the boiling point are smaller than changes in the freezing point for a given solvent. Boiling point elevations are thus more difficult to measure precisely. For this reason, freezing point depression is more commonly used to determine molar mass than is boiling point elevation. Because of its very large value of \(K_f\) (37.8°C/m), d-(+)-camphor (Table \(\PageIndex{1}\)) is often used to determine the molar mass of organic compounds by this method.
Example \(\PageIndex{6}\): Sulfur
A 7.08 g sample of elemental sulfur is dissolved in 75.0 g of \(CS_2\) to create a solution whose freezing point is −113.5°C. Use these data to calculate the molar mass of elemental sulfur and thus the formula of the dissolved \(\ce{S_n}\) molecules (i.e., what is the value of \(n\)?).
Given: masses of solute and solvent and freezing point
Asked for: molar mass and number of \(\ce{S}\) atoms per molecule
Strategy:
- Use Equation \(\ref{13.5.10}\), the measured freezing point of the solution, and the freezing point of \(CS_2\) from Table \(\PageIndex{1}\) to calculate the freezing point depression. Then use Equation \(\ref{13.5.11}\) and the value of \(K_f\) from Table \(\PageIndex{1}\) to calculate the molality of the solution.
- From the calculated molality, determine the number of moles of solute present.
- Use the mass and number of moles of the solute to calculate the molar mass of sulfur in solution. Divide the result by the molar mass of atomic sulfur to obtain \(n\), the number of sulfur atoms per mole of dissolved sulfur.
Solution:
A The first step is to calculate the freezing point depression using Equation \(\ref{13.5.10}\):
\[ΔT_f=T^0_f−T_f=−112.1°C−(−113.5°C)=1.4°C \nonumber\]
Then Equation \(\ref{13.5.11}\) gives
\[m=\dfrac{ΔT_f}{K_f}=\dfrac{1.4° \cancel{C}}{3.74° \cancel{C}/m}=0.37\;m \nonumber\]
B The total number of moles of solute present in the solution is
\[\text{moles solute}=\left(\dfrac{0.37 mol}{\cancel{kg}}\right) (75.0\; g) \left(\dfrac{1 kg}{1000\; g}\right)=0.028 \;mol \nonumber\]
C We now know that 0.708 g of elemental sulfur corresponds to 0.028 mol of solute. The molar mass of dissolved sulfur is thus
\[\text{molar mass}=\dfrac{7.08\; g}{0.028\; mol}=260\; g/mol \nonumber\]
The molar mass of atomic sulfur is 32 g/mol, so there must be 260/32 = 8.1 sulfur atoms per mole, corresponding to a formula of \(\ce{S_8}\).
Exercise \(\PageIndex{6}\)
One of the byproducts formed during the synthesis of \(C_{60}\) is a deep red solid containing only carbon. A solution of 205 mg of this compound in 10.0 g of \(CCl_4\) has a freezing point of −23.38°C. What are the molar mass and most probable formula of the substance?
- Answer
-
847 g/mol; \(\ce{C_{70}}\)
Osmotic Pressure
Osmotic pressure is a colligative property of solutions that is observed using a semipermeable membrane, a barrier with pores small enough to allow solvent molecules to pass through but not solute molecules or ions. The net flow of solvent through a semipermeable membrane is called osmosis (from the Greek osmós, meaning “push”). The direction of net solvent flow is always from the side with the lower concentration of solute to the side with the higher concentration.
Osmosis can be demonstrated using a U-tube like the one shown in Figure \(\PageIndex{6}\), which contains pure water in the left arm and a dilute aqueous solution of glucose in the right arm. A net flow of water through the membrane occurs until the levels in the arms eventually stop changing, which indicates that equilibrium has been reached. The osmotic pressure (\(\Pi\)) of the glucose solution is the difference in the pressure between the two sides, in this case the heights of the two columns. Although the semipermeable membrane allows water molecules to flow through in either direction, the rate of flow is not the same in both directions because the concentration of water is not the same in the two arms. The net flow of water through the membrane can be prevented by applying a pressure to the right arm that is equal to the osmotic pressure of the glucose solution.
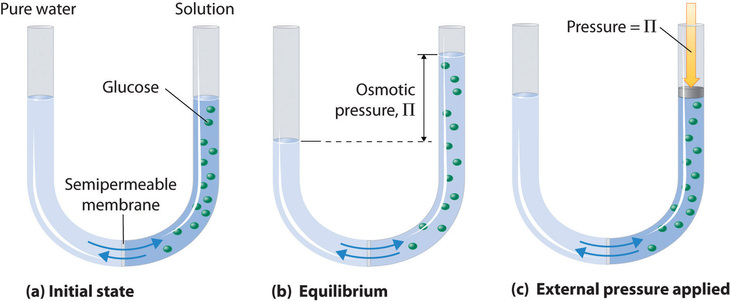
Just as with any other colligative property, the osmotic pressure of a solution depends on the concentration of dissolved solute particles. Osmotic pressure obeys a law that resembles the ideal gas equation:
\[\Pi=\dfrac{nRT}{V}=MRT \label{13.5.12}\]
where \(M\) is the number of moles of solute per unit volume of solution (i.e., the molarity of the solution), \(R\) is the ideal gas constant, and \(T\) is the absolute temperature.
As shown in Example \(\PageIndex{7}\), osmotic pressures tend to be quite high, even for rather dilute solutions.
Example \(\PageIndex{7}\)
When placed in a concentrated salt solution, certain yeasts are able to produce high internal concentrations of glycerol to counteract the osmotic pressure of the surrounding medium. Suppose that the yeast cells are placed in an aqueous solution containing 4.0% \(\ce{NaCl}\) by mass; the solution density is 1.02 g/mL at 25°C.
- Calculate the osmotic pressure of a 4.0% aqueous \(\ce{NaCl}\) solution at 25°C.
- If the normal osmotic pressure inside a yeast cell is 7.3 atm, corresponding to a total concentration of dissolved particles of 0.30 M, what concentration of glycerol must the cells synthesize to exactly balance the external osmotic pressure at 25°C?
Given: concentration, density, and temperature of \(\ce{NaCl}\) solution; internal osmotic pressure of cell
Asked for: osmotic pressure of \(\ce{NaCl}\) solution and concentration of glycerol needed
Strategy:
- Calculate the molarity of the \(\ce{NaCl}\) solution using the formula mass of the solute and the density of the solution. Then calculate the total concentration of dissolved particles.
- Use Equation \ref{13.5.12} to calculate the osmotic pressure of the solution.
- Subtract the normal osmotic pressure of the cells from the osmotic pressure of the salt solution to obtain the additional pressure needed to balance the two. Use Equation \ref{13.5.12} to calculate the molarity of glycerol needed to create this osmotic pressure.
Solution:
A The solution contains 4.0 g of \(\ce{NaCl}\) per 100 g of solution. Using the formula mass of \(\ce{NaCl}\) (58.44 g/mol) and the density of the solution (1.02 g/mL), we can calculate the molarity:
\[ \begin{align*} M_{NaCl} &=\dfrac{moles\; NaCl}{\text{liter solution}} \\[4pt] &=\left(\dfrac{4.0 \; \cancel{g} \;NaCl}{58.44\; \cancel{g}/mol\; NaCl}\right)\left(\dfrac{1}{100\; \cancel{g \;solution}}\right)\left(\dfrac{1.02\; \cancel{g\; solution}}{1.00\; \cancel{mL}\; solution}\right)\left(\dfrac{1000\; \cancel{mL}}{1\; L}\right) \\[4pt] &= 0.70\; M\; \ce{NaCl} \end{align*}\]
Because 1 mol of \(\ce{NaCl}\) produces 2 mol of particles in solution, the total concentration of dissolved particles in the solution is (2)(0.70 M) = 1.4 M.
B Now we can use Equation \ref{13.5.12} to calculate the osmotic pressure of the solution:
\[ \begin{align*} \Pi &=MRT \\[4pt] &=(1.4 \;mol/L)\left[ 0.0821\; (L⋅atm)/(K⋅mol) \right ] (298\; K)\\[4pt] &=34 \;atm\end{align*}\]
C If the yeast cells are to exactly balance the external osmotic pressure, they must produce enough glycerol to give an additional internal pressure of (34 atm − 7.3 atm) = 27 atm. Glycerol is a nonelectrolyte, so we can solve Equation \ref{13.5.12} for the molarity corresponding to this osmotic pressure:
\[ \begin{align*} M&=\dfrac{\Pi}{RT}\\[4pt] &=\dfrac{27\; \cancel{atm}}{[0.0821(L⋅\cancel{atm})/(\cancel{K}⋅mol)] (298 \;\cancel{K})}\\[4pt] &=1.1 \;M \;\text{glycerol} \end{align*}\]
In solving this problem, we could also have recognized that the only way the osmotic pressures can be the same inside the cells and in the solution is if the concentrations of dissolved particles are the same. We are given that the normal concentration of dissolved particles in the cells is 0.3 M, and we have calculated that the \(\ce{NaCl}\) solution is effectively 1.4 M in dissolved particles. The yeast cells must therefore synthesize enough glycerol to increase the internal concentration of dissolved particles from 0.3 M to 1.4 M—that is, an additional 1.1 M concentration of glycerol.
Exercise \(\PageIndex{7}\)
Assume that the fluids inside a sausage are approximately 0.80 M in dissolved particles due to the salt and sodium nitrite used to prepare them. Calculate the osmotic pressure inside the sausage at 100°C to learn why experienced cooks pierce the semipermeable skin of sausages before boiling them.
- Answer
-
24 atm
Because of the large magnitude of osmotic pressures, osmosis is extraordinarily important in biochemistry, biology, and medicine. Virtually every barrier that separates an organism or cell from its environment acts like a semipermeable membrane, permitting the flow of water but not solutes. The same is true of the compartments inside an organism or cell. Some specialized barriers, such as those in your kidneys, are slightly more permeable and use a related process called dialysis, which permits both water and small molecules to pass through but not large molecules such as proteins.
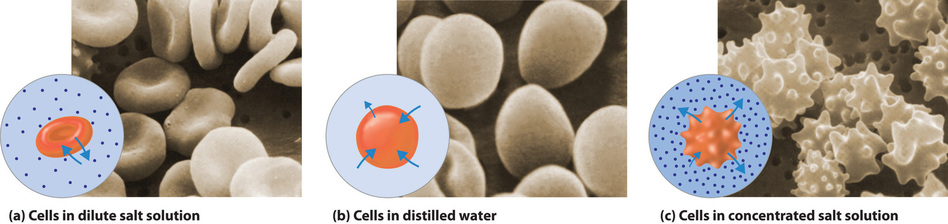
The same principle has long been used to preserve fruits and their essential vitamins over the long winter. High concentrations of sugar are used in jams and jellies not for sweetness alone but because they greatly increase the osmotic pressure. Thus any bacteria not killed in the cooking process are dehydrated, which keeps them from multiplying in an otherwise rich medium for bacterial growth. A similar process using salt prevents bacteria from growing in ham, bacon, salt pork, salt cod, and other preserved meats. The effect of osmotic pressure is dramatically illustrated in Figure \(\PageIndex{7}\), which shows what happens when red blood cells are placed in a solution whose osmotic pressure is much lower or much higher than the internal pressure of the cells.
In addition to capillary action, trees use osmotic pressure to transport water and other nutrients from the roots to the upper branches. Evaporation of water from the leaves results in a local increase in the salt concentration, which generates an osmotic pressure that pulls water up the trunk of the tree to the leaves.
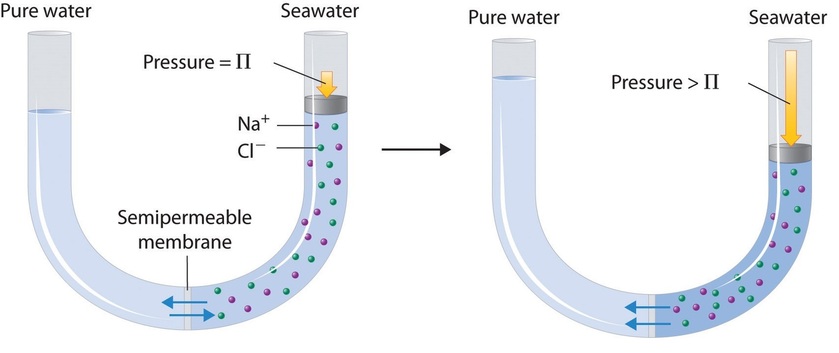
Finally, a process called reverse osmosis can be used to produce pure water from seawater. As shown schematically in Figure \(\PageIndex{8}\), applying high pressure to seawater forces water molecules to flow through a semipermeable membrane that separates pure water from the solution, leaving the dissolved salt behind. Large-scale desalinization plants that can produce hundreds of thousands of gallons of freshwater per day are common in the desert lands of the Middle East, where they supply a large proportion of the freshwater needed by the population. Similar facilities are now being used to supply freshwater in southern California. Small, hand-operated reverse osmosis units can produce approximately 5 L of freshwater per hour, enough to keep 25 people alive, and are now standard equipment on US Navy lifeboats.
Colligative Properties of Electrolyte Solutions
Thus far we have assumed that we could simply multiply the molar concentration of a solute by the number of ions per formula unit to obtain the actual concentration of dissolved particles in an electrolyte solution. We have used this simple model to predict such properties as freezing points, melting points, vapor pressure, and osmotic pressure. If this model were perfectly correct, we would expect the freezing point depression of a 0.10 m solution of sodium chloride, with 2 mol of ions per mole of \(\ce{NaCl}\) in solution, to be exactly twice that of a 0.10 m solution of glucose, with only 1 mol of molecules per mole of glucose in solution. In reality, this is not always the case. Instead, the observed change in freezing points for 0.10 m aqueous solutions of \(\ce{NaCl}\) and \(\ce{KCl}\) are significantly less than expected (−0.348°C and −0.344°C, respectively, rather than −0.372°C), which suggests that fewer particles than we expected are present in solution.
The relationship between the actual number of moles of solute added to form a solution and the apparent number as determined by colligative properties is called the van ’t Hoff factor (\(i\)) and is defined as follows:
\[i=\dfrac{\text{apparent number of particles in solution}}{\text{ number of moles of solute dissolved}} \label{13.5.13}\]
Named for Jacobus Hendricus van ’t Hoff (1852–1911), a Dutch chemistry professor at the University of Amsterdam who won the first Nobel Prize in Chemistry (1901) for his work on thermodynamics and solutions.
As the solute concentration increases, the van ’t Hoff factor decreases.
The van ’t Hoff factor is therefore a measure of a deviation from ideal behavior. The lower the van ’t Hoff factor, the greater the deviation. As the data in Table \(\PageIndex{2}\) show, the van ’t Hoff factors for ionic compounds are somewhat lower than expected; that is, their solutions apparently contain fewer particles than predicted by the number of ions per formula unit. As the concentration of the solute increases, the van ’t Hoff factor decreases because ionic compounds generally do not totally dissociate in aqueous solution.
| Compound | i (measured) | i (ideal) |
|---|---|---|
| glucose | 1.0 | 1.0 |
| sucrose | 1.0 | 1.0 |
| \(NaCl\) | 1.9 | 2.0 |
| \(HCl\) | 1.9 | 2.0 |
| \(MgCl_2\) | 2.7 | 3.0 |
| \(FeCl_3\) | 3.4 | 4.0 |
| \(Ca(NO_3)_2\) | 2.5 | 3.0 |
| \(AlCl_3\) | 3.2 | 4.0 |
| \(MgSO_4\) | 1.4 | 2.0 |
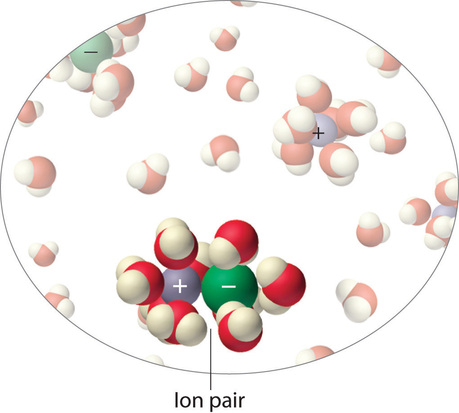
Instead, some of the ions exist as ion pairs, a cation and an anion that for a brief time are associated with each other without an intervening shell of water molecules (Figure \(\PageIndex{9}\)). Each of these temporary units behaves like a single dissolved particle until it dissociates. Highly charged ions such as \(Mg^{2+}\), \(Al^{3+}\), \(SO_4^{2−}\), and \(PO_4^{3−}\) have a greater tendency to form ion pairs because of their strong electrostatic interactions. The actual number of solvated ions present in a solution can be determined by measuring a colligative property at several solute concentrations.
Example \(\PageIndex{8}\): Iron Chloride in Water
A 0.0500 M aqueous solution of \(\ce{FeCl3}\) has an osmotic pressure of 4.15 atm at 25°C. Calculate the van ’t Hoff factor \(i\) for the solution.
Given: solute concentration, osmotic pressure, and temperature
Asked for: van ’t Hoff factor
Strategy:
- Use Equation \(\ref{13.5.12}\) to calculate the expected osmotic pressure of the solution based on the effective concentration of dissolved particles in the solvent.
- Calculate the ratio of the observed osmotic pressure to the expected value. Multiply this number by the number of ions of solute per formula unit, and then use Equation \(\ref{13.5.13}\) to calculate the van ’t Hoff factor.
Solution:
A If \(\ce{FeCl_3}\) dissociated completely in aqueous solution, it would produce four ions per formula unit (one \(\ce{Fe^{3+}(aq)}\) and three \(\ce{Cl^{-}(aq)} ions) for an effective concentration of dissolved particles of 4 × 0.0500 M = 0.200 M. The osmotic pressure would be
\[\begin{align*} \Pi &=MRT \\[4pt] &=(0.200 \;mol/L) \left[0.0821\;(L⋅atm)/(K⋅mol) \right] (298\; K)=4.89\; atm \end{align*}\]
B The observed osmotic pressure is only 4.15 atm, presumably due to ion pair formation. The ratio of the observed osmotic pressure to the calculated value is 4.15 atm/4.89 atm = 0.849, which indicates that the solution contains (0.849)(4) = 3.40 moles of particles per mole of \(\ce{FeCl_3}\) dissolved. Alternatively, we can calculate the observed particle concentration from the osmotic pressure of 4.15 atm:
\[4.15\; atm=M \left( \dfrac{0.0821 \;(L⋅atm)}{(K⋅mol)}\right) (298 \;K) \nonumber\]
or after rearranging
\[M = 0.170 mol \nonumber\]
The ratio of this value to the expected value of 0.200 M is 0.170 M/0.200 M = 0.850, which again gives us (0.850)(4) = 3.40 mole of particles per mole of \(\ce{FeCl_3}\) dissolved. From Equation \(\ref{13.5.13}\), the van ’t Hoff factor for the solution is
\[i=\dfrac{\text{3.40 particles observed}}{\text{1 formula unit}\; \ce{FeCl_3}}=3.40 \nonumber\]
Exercise \(\PageIndex{8}\): Magnesium Chloride in Water
Calculate the van ’t Hoff factor for a 0.050 m aqueous solution of \(\ce{MgCl2}\) that has a measured freezing point of −0.25°C.
- Answer
-
2.7 (versus an ideal value of 3).
Summary
The colligative properties of a solution depend on only the total number of dissolved particles in solution, not on their chemical identity. Colligative properties include vapor pressure, boiling point, freezing point, and osmotic pressure. The addition of a nonvolatile solute (one without a measurable vapor pressure) decreases the vapor pressure of the solvent. The vapor pressure of the solution is proportional to the mole fraction of solvent in the solution, a relationship known as Raoult’s law. The boiling point elevation (\(ΔT_b\)) and freezing point depression (\(ΔT_f\)) of a solution are defined as the differences between the boiling and freezing points, respectively, of the solution and the pure solvent. Both are proportional to the molality of the solute. When a solution and a pure solvent are separated by a semipermeable membrane, a barrier that allows solvent molecules but not solute molecules to pass through, the flow of solvent in opposing directions is unequal and produces an osmotic pressure, which is the difference in pressure between the two sides of the membrane. Osmosis is the net flow of solvent through such a membrane due to different solute concentrations. Dialysis uses a semipermeable membrane with pores that allow only small solute molecules and solvent molecules to pass through. In more concentrated solutions, or in solutions of salts with highly charged ions, the cations and anions can associate to form ion pairs, which decreases their effect on the colligative properties of the solution. The extent of ion pair formation is given by the van ’t Hoff factor (i), the ratio of the apparent number of particles in solution to the number predicted by the stoichiometry of the salt.
- Henry’s law: \[C = kP \nonumber \]
- Raoult’s law: \[P_A=\chi_AP^0_A \nonumber \]
- vapor pressure lowering: \[P^0_A−P_A=ΔP_A=\chi_BP^0_A \nonumber\]
- vapor pressure of a system containing two volatile components: \[P_{tot}=\chi_AP^0_A+(1−\chi_A)P^0_B \nonumber \]
- boiling point elevation: \[ΔT_b = mK_b \nonumber \]
- freezing point depression: \[ΔT_f = mK_f \nonumber\]
- osmotic pressure: \[\Pi=\dfrac{n}{V}RT=MRT \nonumber \]
- van ’t Hoff factor: \[i=\dfrac{\text{apparent number of particles in solution}}{\text{ number of moles of solute dissolved}} \nonumber\]

