10: Weak Acid and Base Equilibria (Worksheet)
- Last updated
- Save as PDF
- Page ID
- 143093
Name: ______________________________
Section: _____________________________
Student ID#:__________________________
Work in groups on these problems. You should try to answer the questions without referring to your textbook. If you get stuck, try asking another group for help.
Learning Objectives
- Understand the role of solvent protolysis in acid-base chemistry
- Understand pH and the pH scale
- Understand the importance of an acid’s or bases’s hydrolysis equilibrium
- Understand the concept of Ka for a weak acid and Kb for a weak base
- Know the relationship between Ka and Kb for a conjugate acid-base pair
- Know the relationships between structure types and acid strength
- a solution of a weak acid or weak base
- Understand the principles of buffer solutions
We have seen that the calculation of [H3O+] and pH for solutions of strong acids and base. To carry out a calculation of all species present in a solution of a pure weak acid in water requires use of the equilibrium constant for the acid’s hydrolysis, called Ka. In similar fashion, calculating the concentrations of all species in a solution of a weak base in water requires solving the equilibrium expression for the bases’s hydrolysis, called Kb. In acid solutions we concentrate on calculating [H3O+] and pH. In basic solutions we concentrate on finding [OH–] and pOH, instead. Some weak bases are the conjugate bases of weak acids. These are generally the anions produced by the acid's hydrolysis. Like molecular bases, these conjugate bases have base hydrolysis equilibria with associated Kb values. The relationship between Ka and Kb for a conjugate acid-base pair allows us to calculate the pH of a solution of either species.
The strengths of acids and their conjugate bases are related to their molecular structures. Knowing the trends allows us to predict whether an acid is strong or weak, and if weak how it compares in strength to other similar weak acids.
Beyond solutions of pure acid or base in water, we need to look at the effect of adding extra amounts of the conjugate base or acid to the solution. The shift in the position of the equilibrium, called the common ion effect, changes the pH and imbues the solution with certain properties that are the basis for formulating a buffer. Buffer solutions are important for regulating pH in many chemical and biological systems.
Success Criteria
- Be able to use \(K_w\) to calculate concentrations of \(\ce{H3O^{+}}\) and \(OH^–\) in acidic or basic solutions
- Be able to calculate \(pH\) and \(pOH\)
- Be able to calculate concentrations of hydronium ion and hydroxide ion in solutions of pure strong acid or strong base in water
- Be able to use \(K_a\) to calculate the concentrations of all species present in a solution of a pure weak acid in water
- Be able to use \(K_b\) to calculate the concentrations of all species present in a solution of a pure weak base in water
- Be able to determine and use \(K_b\) for a conjugate base, given \(K_a\) of its conjugate acid, and vice versa.
- Be able to predict relative strengths of acids or their conjugate bases from structure considerations
Water’s Autoprotolysis
Pure water has an equilibrium with H3O+ and OH– called autoprotolysis or autodissociation.
\[\underbrace{H_2O}_{base_1} + \underbrace{H_2O}_{acid_2} \rightleftharpoons \underbrace{H_3O^+}_{acid_1 } + \underbrace{OH^–}_{base_2} \label{eqA} \]
for which we might write the following equilibrium expression:
\[K_c \equiv K_w = [H_3O^+][OH^–] \nonumber \]
We omit the concentration of \(H_2O(l)\) from the expression, because it is a pure liquid. We can also ignore the concentration of \(H_2O\) for dilute solutions, because \([H_2O]\) is virtually constant. At a temperature of 25 oC, \(K_w\) has a measured value of \(1.0 \times 10^{–14}\):
\[K_w = [H_3O^+][OH^–] = 1.00 \times 10^{–14}\,\, at\, 25 °C \nonumber \]
\(K_w\) is called the ion product or dissociation constant of water. As with all equilibrium constants, \(K_w\) is unitless (as long as concentrations are expressed in molarity).
For pure water, [H3O+] = [OH–]. To find the value of this concentration, let \(x = [H_3O^+] = [OH^–]\) and substitute into the ion product expression for water:
\[K_w = [H_3O^+][OH^–] = 1.0 \times 10^{–14} = x^2 \label{kw} \]
\[x = 1.0 \times 10^{–7}\, M = [H_3O^+] = [OH^–] \nonumber \]
The condition of equal concentration of \(H_3O^+\) and \(OH^-\) defines neutral water, which at 25 °C can be expanded to
\[[H_3O^+] = [OH^–] = 1.0 \times 10^{–7} M \label{eq1} \]
However, since \(K_w\) varies with temperature, then for neutral water at different temperatures:
\[[H_3O^+] = [OH^–] \neq 1.0 \times 10^{–7} M \nonumber \]
The Kw expression in Equation \ref{kw} must be obeyed for any dilute solution in water at at 25 °C. Suppose we add a strong acid, such as HCl, which dissociates completely into H3O+ and Cl– ions. This will increase [H3O+] in the solution, but by Le Chatelier Principle it will cause the autoprotolysis equilibrium (Equation \ref{eqA}) to shift left to maintain a fixed Kw = [H3O+][OH–] = 1.0 x 10–14. This will cause [OH–] to become smaller as more molecular H2O is formed in response to the stress of excess H3O+ ion in the solution.
A strong base, such as NaOH, which dissociates completely into Na+ and OH– ions, would have the reverse effect. This will increase [OH–] in the solution, but it will make [H3O+] smaller as the autoprotolysis equilibrium shifts left to maintain Kw = 1.0 x 10–14. In general, owing to these shifts in the autoprotolysis equilibrium, a solution is acidic if [H3O+] > 10–7 M and [OH–] < 10–7 M, and a solution is basic if [H3O+] < 10–7 M and [OH–] > 10–7 M (at 25 °C).
Q1
Given the following concentrations of H3O+ or OH–, calculate the concentration of OH– or H3O+, and indicate whether the solution is acidic or basic.
| [H3O+] | [OH–] | Acidic or basic? |
|---|---|---|
| 1.0 x 10–5 M | ||
| 4.0 x 10–9 M | ||
| 1.2 x 10–8 M |
pH and pOH
It is often convenient to express [H3O+] and [OH–] by the logarithmic terms pH and pOH, respectively, defined as
\[\begin{align} pH &= –\log_{10} [H_3O^+] \\[4pt] pOH &= –\log_{10} [OH^–] \end{align} \nonumber \]
Note that the symbol "p" in front of any quantity means "negative base-10 logarithm of"; e.g., pKw = –logKw. The relationship between pH and pOH can be derived from Kw.
\[K_w = \ce{[H3O^{+}][OH^{–}]} = 1.0 \times 10^{–14} \nonumber \]
Taking base-10 logarithms of both sides of this equation, we have
\[ \begin{align*} \log_{10} K_w &= \log_{10} \ce{[H3O^{+}][OH^{–}]} \\[4pt] &= \log_{10} \ce{[H3O^{+}] + \log_{10}[OH^{–}]} \\[4pt] &= –14.00 \end{align*} \]
Changing the sign across this equation, we have
\[–\log_{10} K_w = –\log_{10} \ce{[H3O{+}] – \log_{10}[OH^{–}]} = 14.00 \nonumber \]
If we now recognize that the negative logarithm of any quantity X can be designated with the symbol pX, then this equation becomes
\[pK_w = pH + pOH = 14.00 \nonumber \]
For neutral water at room temperature, where
\[\ce{[H3O^{+}] = [OH^{–}]} = 1.0 \times 10^{–7}\, M \nonumber \]
then
\[pH = pOH = 7.00. \nonumber \]
For acidic solutions pH is less than 7, and for basic solutions pH is greater than 7. Note that pOH runs in the opposite sense. For acid solutions pOH is greater than 7, and for basic solutions pOH is less than 7. It is possible to have solutions in which pH or pOH are greater than 14 or less than 0 (i.e., negative).
Significant Figures in pH Calculations
Note that the number of decimal places in a logarithm indicates the number of significant figures in the original number. For example, the base-10 logarithm of 1.45 x 10–15 (3 sig. figs.) is –14.839, where the decimal part indicates the three significant figures. The –14 part (left of the decimal) relates to the power of ten, and has no relevance to significant figures. Why is this? Because we cannot take the logarithm of a negative decimal number, the logarithm–14.839 is actually the sum of a negative integer (–15) and a positive decimal (0.161); i.e., –15 + 0.161 = –14.839. The –15, called the characteristic, relates to the 10–15 of the original number, and the 0.161, called the mantissa, relates to the 1.45 of the original number, which is where the significant digits are. Be sure when calculating pH or pOH that the number of decimal places matches the number of significant figures for the concentration of [H3O+] or [OH–].
Q2
Complete the following table by calculating the missing entries and indicate whether the solution is acidic or basic. Be sure your answers are expressed to the proper number of significant figures.
| [H3O+] | [OH–] | pH | pOH | acidic or basic? |
|---|---|---|---|---|
| 5.8 x 10–5 M | ||||
| 6.2 x 10–6 M | ||||
| 11.24 | ||||
| 9.70 | ||||
| 2.0 M |
Solutions of Strong Acids and Bases
When a strong acid, HA, dissolves in water it dissociates completely into H3O+ and A– ions, leaving no molecular HA in the solution:
\[\ce{HA(aq) + H_2O(l) \rightarrow H_3O^{+}(aq) + A^{–} (aq)} \nonumber \]
Thus, when we talk about the concentration of a strong acid solution, say 0.10 M HCl, we are usually referring to the number of moles per liter used to make the solution, not what is actually present in the solution. Because of dissociation, there is virtually no molecular HCl in a 0.10 M HCl solution! We can define the analytical concentration of the acid HA, symbolized CHA, as the number of moles per liter of acid used to make the solution. Thus, for 0.10 M HCl, CHCl = 0.10 M. Then, using bracket symbols, we can refer to actual concentrations in the solution as [HA], [H3O+], and [A×]. For moderate analytical concentrations of strong acid (CHA >> 10–7 M), we can generally assume that the acid’s dissociation supplies virtually all the H3O+ in the solution; i.e., water’s contribution is insignificant. For a given analytical concentration of a pure strong acid at moderate concentration, we would have the following values initially and after dissociation:
| ICE Table | \(\ce{HA(aq)}\) | \(\ce{H2O}\) | \(\ce{H3O^{+}(aq)}\) | \(\ce{A– (aq)}\) |
|---|---|---|---|---|
| Initial | \(C_{\ce{HA}}\) | - | 0 | 0 |
| Change | \(-C_{\ce{HA}}\) | - | \(+C_{\ce{HA}}\) | \(+C_{\ce{HA}}\) |
After Dissociation |
0 | - | \(C_{\ce{HA}}\) | \(C_{\ce{HA}}\) |
In other words, the concentrations of hydronium ion and conjugate base in the solution are equivalent to the number of moles per liter of acid added to make the solution; i.e.,
\[\ce{[H3O^{+}] = [A^{–}] = } C_{\ce{HA}}. \nonumber \]
Because of complete dissociation there is no equilibrium and \([HA] = 0\).Hence, for 0.10 M HCl, we would have
- \( \ce{[HCl]} = 0\) and
- \( \ce{[H3O^{+}] = [Cl^{–}]} = 0.10\, M\).
In similar fashion, a strong base dissociates completely on dissolving in water. Most strong bases are ionic hydroxide compounds, with the general formula \(\ce{M(OH)_n\), where \(n = 1, 2, 3\), depending on the charge on the cation, Mn+. The number of moles per liter of ionic base used to make the solution, the analytical concentration, can be designated \(C_{M(OH)_n}\). Analogous to the strong acid case, for solutions of pure strong base at moderate analytical concentration (\(C_{M(OH)_n} \ge 10^{–7} M\)), we can generally assume that the base’s dissociation supplies virtually all the \(OH^–\) ion in the solution; i.e., water’s contribution is insignificant. For a given analytical concentration of a pure strong base at moderate concentration, we would have the following values initially and after dissociation:
| ICE Table | \(\ce{M(OH)_{n}}\) | \(\ce{H2O}\) | \(\ce{M^{n+}(aq)}\) | \(\ce{OH– (aq)}\) |
|---|---|---|---|---|
| Initial | \(C_{\ce{M(OH)_{n}}}\) | - | 0 | 0 |
| Change | \(-C_{\ce{M(OH)_{n}}}\) | - | \(+C_{\ce{M(OH)_{n}}}\) | \(+ n C_{\ce{M(OH)_{n}}}\) |
After Dissociation |
0 | - | \(C_{\ce{M(OH)_{n}}}\) | \( n C_{\ce{M(OH)_{n}}}\) |
In other words, the concentration of hydroxide ion and cation in the solution are equivalent to the number of moles per liter of base used to make the solution, factoring in the stoichiometry of the dissociation; i.e.,
- \(\ce{[OH^{–}]} = nC_{\ce{M(OH)_{n}}}\),
- \(\ce{[Mn^{n+}]} = C_{\ce{M(OH)_{n}}}\),
- \(\ce{[MnOH_{n}]} = 0\).
This is because of complete dissociation. For any acid solution, once \(\ce{[H3O^{+}]}\) is determined,
\[\ce{ [OH^{–} ] = \dfrac{K_w}{ [H3O^{+}]}}. \label{eq10A} \]
Likewise, for any base solution, once \(\ce{[OH^{–}]}\) is determined then
\[\ce{ [H3O+ ] = \dfrac{K_w}{ [OH^{–}]}}.\label{eq10B} \]
Q3
Determine the concentrations of \(\ce{H3O^{+}}\) and \(\ce{OH^{–}}\) in the following solutions of strong acids or bases in water. [Caution: Think about how the acid or base dissociates in water.]
| Solution | [OH–] | Acidic or basic? |
|---|---|---|
| \(2.5 \times 10^{–3}\, M\) of \(HCl\) | ||
| \(0.0010\, M\) of \(NaOH\) | ||
| \(7.5 \times 10^{–5}\, M\) of \(Ca(OH)_2\) |
Weak Acid Hydrolysis
All acids in water have an acid hydrolysis equilibrium that produces hydronium ion and the conjugate base of the acid:
\[\ce{HA + H2O <=> H3O^{+} + A^{–} } \nonumber \]
With strong acids this equilibrium lies completely to the right. With weak acids, the equilibrium lies to the left, which means that undissociated acid, \(\ce{HA}\), is usually the principal species in the solution, with only relatively small concentrations of H3O+ and A– produced from the hydrolysis reaction. The equilibrium constant for the hydrolysis of an acid is labeled \(K_a\), defined as
\[K_a = \ce{\dfrac{[H3O^{+}][A^{-}]}{[HA]}} \label{KaWeak} \]
\(K_a\) is a constant for a given acid at a particular temperature regardless of the number of moles per liter of acid that was dissolved (the analytical concentration of the acid) to make the solution.
We can use \(K_a\) to calculate the equilibrium concentrations of all species involved in the hydrolysis reaction (undissociated acid, hydronium ion, and conjugate base) in a solution of a pure weak acid in water. We will only deal with solutions at moderate concentrations, in which we can assume that the added acid is the principal source of hydronium ion. Therefore, we will assume that prior to adding acid we have \(\ce{[H3O^{+}]} = 1.0 \times 10^{–7}\, M \approx 0\, M\). To set up the problem, let x be the concentration of hydronium ion, \(\ce{[H_3O^{+}]}\), produced by the acid’s hydrolysis once equilibrium is established. Then, for an initial concentration of acid \(\ce{HA}\), symbolized here as \(C_{\ce{HA}}\), at equilibrium we have
| ICE Table | \(\ce{HA(aq)}\) | \(\ce{H2O}\) | \(\ce{H3O^{+}(aq)}\) | \(\ce{A^{–} (aq)}\) |
|---|---|---|---|---|
| Initial | \(C_{\ce{HA}}\) | - | ~0 | 0 |
| Change | \(-x\) | - | \(+x\) | \(+x\) |
| Equilibrium | \(C_{\ce{HA}} - x\) | - | \(x\) | \(x\) |
If we substitute the algebraic expressions for all the equilibrium concentrations into \(K_a\) (Equation \ref{KaWeak}), we have
\[K_a = \ce{\dfrac{[H3O^{+}][A^{-}]}{[HA]}} = \dfrac{x^2}{C_{\ce{HA}} - x} \nonumber \]
This is gives the quadratic equation (in standard form),
\[x^2 + K_a x – K_a C_{\ce{HA}} = 0 \label{quadacid} \]
where \(a =1\), \(b = K_a\), and \(c = –K_a C_{\ce{HA}}\). Solving the quadratic and ignoring the negative root, we obtain
\[x = \ce{[H3O^{+}] = [A^{–}]}. \nonumber \]
Then, we can solve
\[\ce{[HA]} = C_{\ce{HA}} – x \label{exact1} \]
to obtain the concentration of undissociated acid in the solution.
Approximate Solutions
Very often we can make some simplifying assumptions that make it unnecessary to solve a quadratic equation (although with poorer accuracy). When the acid is very weak (very small \(K_a\) value) or its analytical concentration is relatively large (\(C_{\ce{HA}} \gg K_a\)), the amount of dissociation of molecular \(\ce{HA}\) may be very small. Put another way, we could say
\[C_{\ce{HA}} \gg x. \nonumber \]
Thus, in such cases we can often ignore \(x\) in parts of the equation
\[\ce{[HA]} = C_{\ce{HA}} – x \approx C_{\ce{HA}} \nonumber \]
| ICE Table | \(\ce{HA(aq)}\) | \(\ce{H2O}\) | \(\ce{H3O^{+}(aq)}\) | \(\ce{A^{–} (aq)}\) |
|---|---|---|---|---|
| Initial | \(C_{\ce{HA}}\) | - | ~0 | 0 |
| Change | \(-x\) | - | \(+x\) | \(+x\) |
| Equilibrium | \(~C_{\ce{HA}}\) | - | \(x\) | \(x\) |
Substituting our simplified algebraic expressions into the \(K_a\) expression (Equation \ref{KaWeak}), we have
\[K_a = \ce{\dfrac{[H3O^{+}][A^{-}]}{[HA]}} \approx \dfrac{x^2}{C_{\ce{HA}}} \nonumber \]
from which it follows
\[x = \sqrt{K_aC_{\ce{HA}} } = \ce{[H3O^{+}] = [A^– ].} \label{approx1} \]
As a practical matter, because it takes so little time to calculate, try using \(x= \sqrt{K_aC_{\ce{HA}} } \) and then calculate the percent dissociation as
\[\% \, \text{dissociation} = \dfrac{\ce{[H3O^{+} ]}}{C_{\ce{HA}}} \times 100\% \nonumber \]
If this calculation gives an answer of less than 5%, the calculated values of \(\ce{[H3O^{+} ]}\) and \(\ce[A^{–}]}\) are reasonably accurate and can be accepted. If this calculation gives a value that is greater than 5%, then the acid’s dissociation is too great to ignore in the algebraic expression for [HA]. Then, go back and use the more exact expression (Equation \ref{exact1})
\[\ce{[HA]} = C_{\ce{HA}} – x \nonumber \]
which means you must solve the quadratic equation. Usually, if \(C_{\ce{HA}} \gg K_a\) by two powers of 10 or more, the acid is probably not appreciably dissociated and you can use (Equation \ref{approx1})
\[\ce{ [H3O^{+}] } = \sqrt{K_a C_{\ce{HA}} } \nonumber \]
But be sure to check your method by calculating the percent dissociation. If \(C_{\ce{HA}} \approx K_a\) (within two powers of 10), you will probably have to solve the quadratic equation. By either method, once \(\ce{[H3O^{+}]}\) has been calculated, the concentration of hydroxide ion in the solution can be determined by solving the \(K_w\) expression (Equation \ref{eq10A}):
\[ \begin{align} [ \ce{OH^{-}} ] &= \dfrac{K_w} { [\ce{ H3O^{+}} ] } \\[5pt] &= \dfrac{1.00 \times 10^{-14} }{ [ \ce{ H3O^{+}} ]} . \end{align} \nonumber \]
Q4
A 0.0100 M solution of a weak acid HA has a pH of 2.60. What is the value of \(K_a\) for the acid? [Hint: What is the actual concentration of undissociated \(\ce{HA}\), i.e., \(\ce{[HA]}\), in this solution?]
Q5
What is the pH of \(4.0 \times 10^{–2}\, M\) benzoic acid (\(\ce{C6H5CO2H}\) = \(\ce{HBz}\)), for which \(K_a = 6.46 \times 10^{–5}\)? Is it necessary to solve the quadratic equation in this case?
Q6
Find the concentrations of all species and pH for a \(1.0 \times 10^{–3}\, M\) \(HF\) solution (\(K_a = 6.7 \times 10^{–4}\). You will need to find values for \(\ce{[HF]}\), \(\ce{[H3O^{+}]}\), \(\ce{[F^{–}]}\), and \(\ce{[OH^{–}]}\).
Weak Base Hydrolysis
When a weak base like ammonia is added to water it hydrolyzes to give small amounts of hydroxide ion and its conjugate acid in water. If we symbolize weak bases as \(\ce{B}\), then the general hydrolysis equilibrium is
\[\ce{B + H2O <=> BH^{+} + OH^{–} } \nonumber \]
for which we can write the equilibrium constant expression
\[K_b = \ce{ \dfrac{[BH^{+}][OH^{–}]}{[B]} } \label{KbWeak} \]
We can use \(K_b\) to calculate the concentrations of all species in the solution in a manner analogous to the way we used Ka for weak acid solutions. However, with base solutions we focus on determining \(\ce{[OH^{–}]}\) first, rather than \(\ce{[H3O^{+}]}\). Once we have determined \(\ce{[OH^{–}]}\), we can use
\[K_w = \ce{[H3O^{+}][OH^{–} ]} = 1.0 \times 10^{–14} \nonumber \]
to calculate \(\ce{[H3O^{+}]}\) and pH.
For a solution of a pure weak base in water with a moderate analytical concentration, \(C_{\ce{B}}\), we would have the following concentrations initially and at equilibrium:
| ICE Table | \(\ce{B(aq)}\) | \(\ce{H2O}\) | \(\ce{BH^{+}(aq)}\) | \(\ce{OB^{–} (aq)}\) |
|---|---|---|---|---|
| Initial | \(C_{\ce{HA}}\) | - | ~0 | 0 |
| Change | \(-x\) | - | \(+x\) | \(+x\) |
| Equilibrium | \(C_{\ce{HA}} - x\) | - | \(x\) | \(x\) |
Substituting into the \(K_b\) expression, we obtain
\[K_b = \ce{\dfrac{[BH^{+}][OH^{-}]}{[B]}} = \dfrac{x^2}{C_{\ce{B}}-x} \nonumber \]
This is a quadratic equation of the form
\[x^2 + K_b x – K_b C_{\ce{B}} = 0. \label{truebase} \]
Notice that this is virtually the same equation we obtained in the weak acid case (Equation \ref{quadacid}), except here
\[x = \ce{[BH^{+} ]} = \ce{[OH^{– }]} \nonumber \]
and of course we have \(K_b\) instead of \(K_a\). As with the acid case, if the analytical concentration of the base is relatively large (\(C_{\ce{B}} \gg K_b\)), hydrolysis may be minimal and we can ignore \(x\) in the Equation \ref{truebase} for \(\ce{[B]}\); i.e.,
\[[B] = C_{\ce{B}} – x \approx C_{\ce{B}} . \nonumber \]
Then, the equation above simplifies to
\[K_b = \ce{\dfrac{[BH^{+}][OH^{-}]}{[B]}} \approx \dfrac{x^2}{C_{\ce{B}}} \nonumber \]
from which it follows
\[ x = \sqrt{C_{\ce{B}} K_b } = \ce{[OH^{-}]} = \ce{[BH^{+}]} \nonumber \]
Analogous to the acid case, if \(C_{\ce{B}} \gg K_b\) by two or more powers of 10, then this simplified equation probably can be used. If CB . Kb, within two powers of 10, then the quadratic equation will probably need to be solved. If the simplified equation is used, check its validity by calculating the percent hydrolysis of the base:
\[\% \, \text{hydrolysis} = \dfrac{\ce{[OH^{-} ]}}{C_{\ce{B}}} x 100\% \nonumber \]
If this calculation gives 5% or greater, use the more exact expression
\[[B] = C_{\ce{B}} – x \nonumber \]
and solve the quadratic equation. By either method, once [OH– ] has been calculated, use
\[K_w = \ce{[H3O^{+} ][OH^{–} ]} = 1.0 \times 10^{–14} \nonumber \]
to calculate \(\ce{[H3O^{+}]}\) and
\[pH + pOH = 14.00 \nonumber \]
to calculate pH.
Q7
What is the pH of a 0.120 M solution of \(NH_3(aq)\)? For ammonia, \(K_b = 1.77 \times 10^{–5}\). Is it necessary to solve the quadratic equation? Justify the approach you took, either way.
Kb of Conjugate Bases and Ka of Conjugate Acids
The conjugate base of a strong acid has little tendency to acquire \(\ce{H^{+}}\) and reform the acid. Thus, \(\ce{Cl^{-}}\), the conjugate base of \(\ce{HCl}\), has virtually no real base strength. But the conjugate bases of weak acids do have a tendency to acquire \(H^+\), and so they are real weak bases. Like any other weak base, they have a base hydrolysis equilibrium and a related Kb. For example, consider a weak acid \(\ce{HA}\) and its conjugate base \(\ce{A^{–}}\). The two are related to each other by the acid's hydrolysis equilibrium:
\[\ce{HA + H_2O \rightleftharpoons H_3O^{+} + A^{–}} \nonumber \]
with
\[K_a= \ce{\dfrac{[H_3O^{+}][A^{-}]}{[HA]}} \nonumber \]
But they are also related to each other by the conjugate base's hydrolysis equilibrium:
\[\ce{A^{–} + H_2O \rightleftharpoons HA + OH^{–} } \nonumber \]
with
\[K_b=\ce{\dfrac{[HA][OH^-]}{[A^{-}]}} \nonumber \]
How is the value of \(K_a\) of \(\ce{HA}\) related to the value of \(K_b\) of \(A^–\)? Recall that when two equilibria are added together the equilibrium constant for the sum is the product of the individual equilibrium constants. If we add the acid hydrolysis equilibrium of \(HA\) and the base hydrolysis equilibrium of \(A^–\), the sum is
\[\ce{2 H_2O \rightleftharpoons H_3O^{+} + OH^{–}} \nonumber \]
which is water's autoprotolysis equilibrium (Equation \ref{eqA}), governed by \(K_w\):
| Reaction | Equilibrium Constant |
|---|---|
| \(\ce{HA + H2O <=> H3O^{+} + A^{–}}\) | \(K_a= \ce{\dfrac{[H_3O^{+}][A^{-}]}{[HA]}}\) |
| \(\ce{A^{–} + H2O <=> HA + OH^{–}}\) | \(K_b=\ce{\dfrac{[HA][OH^-]}{[A^{-}]}}\) |
| \(\ce{2 H2O <=> H3O^{+} + OH^{–}}\) | \( \begin{align} K_a \times K_b &= \ce{\dfrac{[H_3O^{+}][A^{-}]}{[HA]}} \ce{\dfrac{[HA][OH^-]}{[A^{-}]}} \nonumber\\ &= \ce{[H3O^{+}][OH^{-}]} = K_w \nonumber \end{align} \nonumber\) |
Therefore, in general we can write
\[ K_a^{HA}K_b^{A^-} = K_w \label{acid} \]
Similarly, if we have a molecular base \(\ce{B}\) with known \(K_b\), its conjugate acid \(\ce{BH^{+}}\) would have a \(K_a\) given by
\[ K_b^{B}K_a^{BH^+} = K_w \label{base} \]
As these relationships show, the larger the value of \(K_a\) for an acid, the smaller the value of \(K_b\) will be for its conjugate base, and vice versa.
Conjugate bases of weak acids are true bases. For example, the acetate ion (often abbreviated OAc–), which is the conjugate base of acetic acid (often abbreviated HOAc), can make a basic solution as a result of its base hydrolysis. The \(K_b\) value for the acetate ion can be calculated from acetic acid's \(K_a = 1.78 \times 10^{–5}\), using Equation \ref{acid}.
\[\ce{OAc^{–} + H2O <=> HOAc + OH^{–}} \nonumber \]
But we cannot simply add acetate ions to a solution. They must be supplied in the form of an ionic salt, such as sodium acetate, which dissociates completely in water to give an equivalent amount of acetate ion and sodium ion in solution. Sodium ion has no acid-base character, so the pH of the solution is the result of the acetate ion's base hydrolysis:
\[\begin{align} \ce{NaOAc} \rightarrow \ce{Na^+} + \, & \ce{OAc^–} \\ & \ce{OAc^{–}} + \ce{H2O} \ce{<=>} \ce{HOAc} + \,\ce{OH^{–}} \end{align} \nonumber \]
at pH > 7.
In similar manner, we can create a solution of the conjugate acid of a molecular weak base by adding one of its soluble salts, such as a chloride. For example, ammonium chloride,\(\ce{ NH4Cl}\), when dissolved in water supplies an equivalent amount of ammonium ion, \(\ce{NH4^{+}}\), the conjugate acid of ammonia, and chloride ion. The chloride ion, being the conjugate base of a strong acid (\(\ce{HCl}\)) has no real acid-base character, so the pH of the solution is the result of the ammonium ion's acid hydrolysis:
\[\begin{align} \ce{NH_4^{+}Cl} \rightarrow \ce{Cl^{-}} + \, &\ce{NH4^{+}} \\ &\ce{NH_4^{+}} + \ce{H_2O} \rightleftharpoons \ce{NH_3} +\, \ce{H3O^{+}} \end{align} \nonumber \]
this results in a solution with a pH < 7.
The \(K_a\) for the ammonium ion can be calculated from \(K_b = 1.77 \times 10^{–5}\) for ammonia.
\[NH_4^+ + OH^{ -} \rightleftharpoons NH_3 + H2O \nonumber \]
with
\[K_a^{NH_4^+} = \dfrac{K_w}{K_b^{NH_3}} = \dfrac{ 1.00 \times 10^{-14}}{1.77 \times 10^{-5}} = 5.65 \times 10^{-10} \nonumber \]
Q8
Sodium hypochlorite, \(\ce{NaOCl}\), is the active ingredient in chlorine bleach (e.g., Chlorox). For hypochlorous acid, \(\ce{HOCl}\) with \(K_a = 3.0 \times 10^{-8}\).
- Write the equation for the base hydrolysis equilibrium of the hypochlorite ion.
- What is the value of \(K_b\) for the hypochlorite ion?
- What is the pH of a 0.10 M solution of sodium hypochlorite?
Q9
Trimethylamine, \((CH_3)_3N\), is a weak base (\(K_b = 6.4 \times 10^{–5}\)) that hydrolyzes by the following equilibrium:
\[\ce{(CH3)3N + H2O \rightleftharpoons (CH3)3NH^{+} + OH^{–}} \nonumber \]
- Write the equation for the acid hydrolysis equilibrium of trimethylammonium ion, \(\ce{(CH3)3NH^{+}}\).
- What is the value of \(K_a\) for the trimethylammonium ion, \(\ce{(CH3)3NH^{+}}\)?
- What is the pH of a 0.12 M solution of trimethylammonium chloride, \(\ce{((CH3)3NH)Cl}\)?
Acid Strength and Structure
The tendency of an acid to lose a proton to solvent water, as indicated by its \(K_a\) value, depends upon two principal factors:
- The strength of the \(H–A\) bond. The weaker the bond, the greater is the tendency to lose protons, and the larger \(K_a\) will be.
- The stability of the conjugate base in solution. The more stable the conjugate base \(A^–\), the greater is the tendency of \(HA\) to lose protons, and the larger \(K_a\) will be.
For simple inorganic acids, the first factor is more important. The second factor is often important in comparisons among organic acids.
Acid strengths of binary acids, with the general formula \(H_nX\), increase as the \(H–X\) bond weakens. This results in the following trends:
- The larger the X atom, the weaker the H–X bond is and the stronger the acid is.
\[\ce{HF < HCl < HBr < HI < H_2O < H_2S < H_2Se < H_2Te} \nonumber \]
- Among acids with similar \(H–X\) bond strengths, the more electronegative the \(X\) atom, the more polar the \(H–X\) bond will be. This makes the \(H\0 atom more positive, facilitating its removal by solvent water. Thus, across a period,
\[\ce{NH_3 < H_2O < HF} \nonumber \]
One of the most studied groups of acids is the family of oxyacids, with the general formula \(HOXO_n\), where \(X\) is a central atom. In these acids, the acidic hydrogen is always bonded to an oxygen atom, with a linkage of the type \(X–O–H\). Any hydrogen atoms bonded directly to the central \(X\) atom (i.e., X–H) are not acidic. These acids may also have one or more terminal oxygen atoms, bonded directly to \(X\) but not bearing a hydrogen atom (i.e. \(X–O\)). In most oxyacids (with some exceptions) there are no X–H bonds, so the number of terminal oxygen atoms is just the total number of oxygen atoms minus the number of hydrogen atoms in the formula. Thus, \(HClO_3\) has two terminal oxygen atoms, with the third oxygen atom bonded to the acidic hydrogen atom. The number of these terminal oxygen atoms affects the acid’s strength. In general, two factors are important in judging the strengths of oxyacids:
- Among acids of the same structure type, acid strength increases with the electronegativity of the central X atom. For example, \[\ce{HOI < HOBr < HOCl < H_2SeO_4 < H_2SO_4} \nonumber \] As electronegativity of \(X\) increases, the polarity of the \(–O–H\) bond increases, making removal of \(H^+\) by solvent water more favorable.
- Acidity increases as the number of terminal oxygen atoms (those without H attached to them) increases. For example,\[ \ce{HOCl < HOClO < HOClO2 < HOClO3} \nonumber \] The electron withdrawing ability of the terminal –O atoms increases the formal charge on the central X atom, decreasing electron density in the –O–H bond, thereby weakening it. This is an example of an inductive effect.
The number of terminal oxygen atoms in the oxyacids bears a strong correlation to \(K_a\).
| \(-O\) atoms | \(K_a\) Range | Strength |
|---|---|---|
| 0 | \(10^{-7} - 10^{-10}\) | very weak |
| 1 | \(10^{-1} - 10^{-4}\) | weak |
| 2 | \(> 10^{-1}\) | strong |
| 3 | \(\gg 1\) | very strong |
An important group of organic acids contains the carboxyl group, \(-CO_2H\). Accordingly, such acids are called carboxylic acids.
| \(\ce{HCO2H}\) | \(\ce{CH3CO2H }\) | \(\ce{CH3CH2CO2H }\) | \(\ce{CH3CH2CH2CO2H }\) | \(\ce{HO2CCO2H }\) |
| formic acetic | acetic | propionic | butyric | oxolic (diprotic) |
The acidity of the carboxyl group is partly due to the electronegativity of the double-bonded oxygen, which withdraws electron density from the \(–O–H\) bond, thereby facilitating the loss of \(H^+\) to solvent water. Furthermore, when a carboxyl group loses \(H^+\), it forms a resonance stabilized anion, called a carboxylate ion:
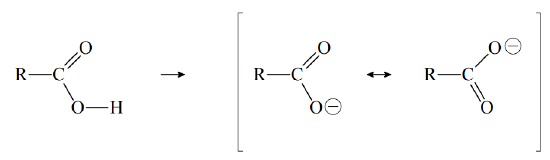
(The symbol R represents the rest of the organic molecule.) The acidity of a carboxylic acid can be enhanced by adding electronegative atoms to the rest of the molecule. The electron-withdrawing ability of such atoms weakens the \(–O–H\) bond (inductive effect), thereby enhancing the ability of solvent water to remove \(H^+\). For example, \(Cl_3CCO_2H\) is a much stronger acid than \(CH_3CO_2H\).
Q10
Explain the following observations:
- \(H_2Se\) is a stronger acid than \(H_2S\)
- \(HNO_2\) is a weak acid, but \(HNO_3\) is a strong acid
- \(H_3PO_4\) is a stronger acid than \(H_3AsO_4\)
- \(FCH_2CO_2H\) is a stronger acid than \(CH_3CO_2H\)


